第3部 射影幾何から双曲幾何へ
Ch.41 クロスキャップ (2) 
これまでとは逆に、メビウスの帯に円板をかぶせてクロスキャップをつくることを具体的にこころみます。
物理的に円板をメビウスの帯に貼りあわせることが不可能なことは、すこし目で追ってみればわかります。 しかし、それは頭の中でのイメージ操作です。 その意味では、たよりない。 実際にどこでどう不可能なのかをつぶさにたぐってみます。
その道すがら目次の横にあった妙なものに出くわします。
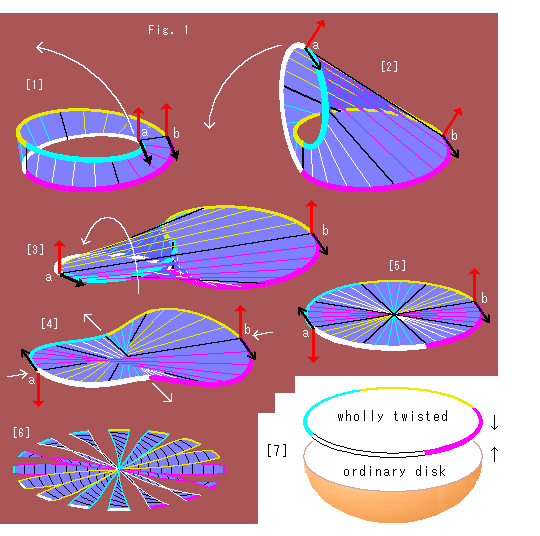 Fig.1をご覧ください。
Fig.1をご覧ください。
メビウスの帯を円板にするとどうなるでしようか。
[1]: 観察の便のために、縁を四つに色分けして、面には筋を入れています。 赤い矢印は局所的な面に立てた法線ベクトルです。 黒い矢印は縁の接線ベクトルです。
bのところを固定しておいて、aの方を白い矢印のように左上へ引き伸ばします。 面はよく伸びるゴム製だと想ってください。
[2]: さらに左下へと曲げます。
[3]: 平坦にしたところです。 白い矢印の方向にaの側をひねって、縁の捻じれをときます。
[4]: 縁の捻じれがとけたかわりに、左の方では面の向きが逆になりました。 そして、赤と黒のベクトルがaとbでは逆向きになっています。 白い矢印のように四方を伸縮して、円形になるようにしていきます。 すると、面のよじれが片寄らなくなってきます。
[5]: メビウスの帯が円板になりました。 メビウスの帯には穴がありますが、この円板には穴はありません。 きれいな円板に見えています。 けれども、その面は捻じれたままなのです。 メビウスの帯は切断しないかぎり、どんなに変形しても表裏のないものであることに変わりはないのですから、当然ですね。 ですから、コインの表裏のようなものを想わないでください。
[6]: 円板を扇を裂くように隙間をとって見れば、このようになっていると思えますが、そうではありません。 ちょっと考えにくいですが、すべての方向に全体として、180 捻じれているのです。
捻じれているのです。
[7]: この全体が捩れた(wholly twisted)円板であるメビウスの帯にふつうの円板(ordinary disk)を椀状のままでかぶせることは簡単です。 けれども、はっきりと見える姿に描けません。
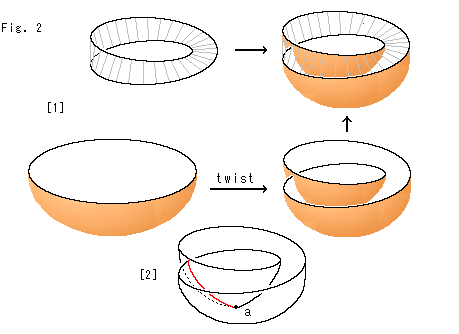
Fig.2をご覧ください。
メビウスの帯はさわらずに、円板の方を変形してみます。
[1]: 自己交差をゆるして、円板を椀状のままで捻じり(twist)、その縁がメビウスの帯の縁と合うようにします。 その捩れた円板は、メビウスの帯に貼り合わせることができます。 その際、両者が交差してもよいとします。 すると、すべてが具体的におこなえます。 交差線での扱いは、クロスキャップと同様にします。 完成品は、私たちの目で見ることのできるものです。
しかし、できたものはクロスキャップとは違って、閉曲面ではありません。 クロスキャップにするには、手術が必要です。
[2]: 赤い線は、捩れた円板の自己交差の交線です。 交差を禁止する規則はありません。 それはよいのですが、問題が一つあります。 椀状の円板の下端aです。 そこを這う点の動きは定めようがありません。 それを逃れるために、点aは例外で、特異点としてあつかうことにします。
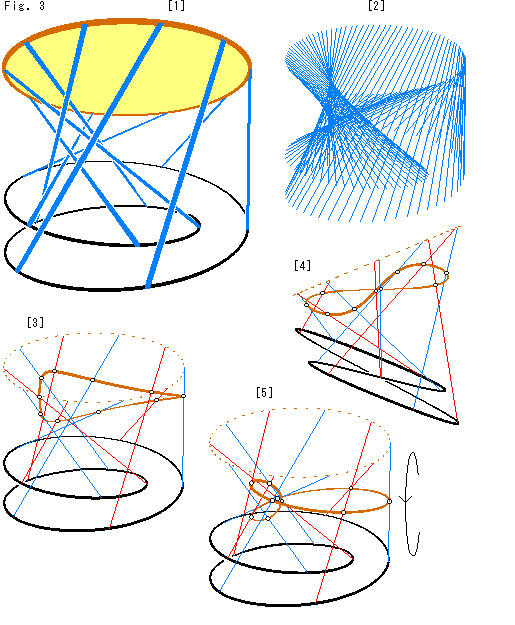
Fig.3をご覧ください。
[1]: 黄色い円板は、ふつうの円板です。 青い線は、貼り合わせる対応点をむすんだものです。 メビウスの帯(Mobius strip)と円板(disk)頭文字をとって、この青い線をMD対応線とよんでおきます。 私たちの新案です。
[2]: MD対応線だけを無数に描いたものです。 捩れた円筒のようになっています。 円板をメビウスの帯にぴったりかぶせなくても、このような対応を想って、それを「かぶせた」と考えてもよいですね。
[3]: MD対応線を見分けやすいように、交互に赤色と青色にします。 そうすると、メビウスの帯の縁の向かい合った点のMD対応線が赤と青のペアになります。
MD対応線を固定して、円板を動かすレールにします。 図は、そうしておいて、円板をすこし下へ動かしたところです。 変な形になっていますね。
[4]: [3]を左から見たものです。 円板がすこし捩れています。 [3]とくらべると、同じ歪みの円板が 見る向きによって、こんなにも違って見えるのです。
[5]: MD対応線の中ほどまで円板を滑らせたところです。 ずいぶん妙な格好になりました。 どこがどうなっているのか、直ぐには見て取れませんね。 これは円板が、捩れていくと同時に、メビウスの帯が置かれている平面に平行になろうとして、矢印のようにこちら側がうつむきの回転をするからです。
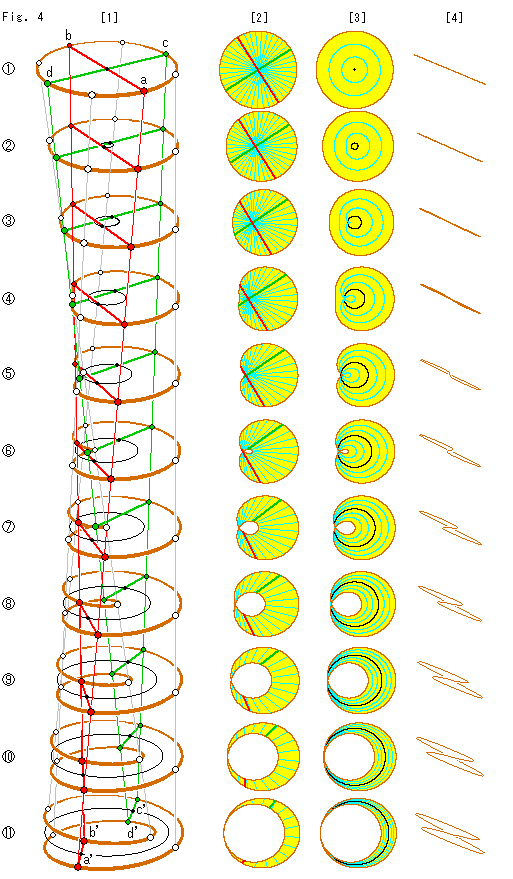 Fig.4をご覧ください。
Fig.4をご覧ください。
丈を伸ばしたMD対応線に沿わせて円板とメビウスの帯を動かします。 そろばん玉のように動くのです。 円板とメビウスの帯は変形自在なものだとします。 たとえば、この円板の面は無数のゴム糸のような直径からできていると想います。 そして、すべての直径の中点は、中心という1個の共有点に固定されているものではないとします。 ですから、それぞれの直径が動けば、それとともに中点も動きます。
円板は下へ行くほど歪んできますが、それでも便宜的に"円板"とよぶことにします。 直径もずれ動きますが、ずっと"直径"とよんでおきます。
[1]: メビウスの帯をMD対応線の下端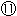 に置いて、円板を上の
に置いて、円板を上の から下へと動かします。 見やすいように、最初に円板とメビウスの帯の傾斜を等しくしておきます。 円板をFig.3のように回転させないためです。 赤と緑の線分は、はじめの
から下へと動かします。 見やすいように、最初に円板とメビウスの帯の傾斜を等しくしておきます。 円板をFig.3のように回転させないためです。 赤と緑の線分は、はじめの で直交していた直径です。 それが、メビウスの帯の向かい合った点をむすぶ線分になります。 黒い線は、無数の直径の中点をなぞったものです。 それは、
で直交していた直径です。 それが、メビウスの帯の向かい合った点をむすぶ線分になります。 黒い線は、無数の直径の中点をなぞったものです。 それは、 では円板の中心でした。 それがメビウスの帯のセンターラインになります。
では円板の中心でした。 それがメビウスの帯のセンターラインになります。
円板がメビウスの帯に変わるのは、 のあたりです。 その後は、与えられたメビウスの帯
のあたりです。 その後は、与えられたメビウスの帯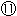 の形になっていくだけです。 メビウスの帯を下から動かしていくときは、
の形になっていくだけです。 メビウスの帯を下から動かしていくときは、 で円板に変わります。
で円板に変わります。
そこは注目されるところなので、あとで詳しくしらべます。
[2]: 各円板をその真上から見たものです。 [1]の約1/2に描いてあります。 水色の線は無数の直径です。 この直径をメビウスの帯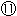 で見ると、その数が半分になっているように見えますが、そうではありません。 直径の数は半径の数の半分ですから、こうなるのです。
で見ると、その数が半分になっているように見えますが、そうではありません。 直径の数は半径の数の半分ですから、こうなるのです。
円板が ではハート形に見えていますが、実際は[1]でわかるように、そこは円板の縁がコイル状になりはじめるところです。
ではハート形に見えていますが、実際は[1]でわかるように、そこは円板の縁がコイル状になりはじめるところです。
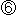 では、小さな穴ができて、上から見て交わっていた赤と緑の直径がはっきりと離れています。
では、小さな穴ができて、上から見て交わっていた赤と緑の直径がはっきりと離れています。  になると、はじめに直交していた赤と緑の直径が直線状に並んでいます。
になると、はじめに直交していた赤と緑の直径が直線状に並んでいます。
途中で円板がすこし小さくなっているのは、MD対応線の束が途中でややしぼんでいるためです。
[3]: こんどは、同心円です。  の黒い点は円板の中心です。
の黒い点は円板の中心です。  では、その中心が黒いループになっています。
では、その中心が黒いループになっています。  になると、水色の内側の同心円が黒いループの中へ回り込んできます。 水色の曲線は、もう同心円ではありませんが、便宜的につづけて同心円とよんでおきます。
になると、水色の内側の同心円が黒いループの中へ回り込んできます。 水色の曲線は、もう同心円ではありませんが、便宜的につづけて同心円とよんでおきます。  のあたりで、黒いループが円板の縁に接します。 そして、水色の同心円のすべてが黒いループ内に回り込んでいます。
のあたりで、黒いループが円板の縁に接します。 そして、水色の同心円のすべてが黒いループ内に回り込んでいます。  になると、円板の縁も黒いループ内に入り込んできます。 つまり、同心円の数が2倍になっているのです。
になると、円板の縁も黒いループ内に入り込んできます。 つまり、同心円の数が2倍になっているのです。
[4]: [1]の各円板を1/2に縮小して、真左から見たものです。
このFig.4へは、末尾で立ち戻ります。
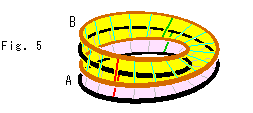 Fig.5をご覧ください。
Fig.5をご覧ください。
下側のメビウスの帯Aは、MD対応線の下端に与えられているものです。 そこへ降りてくる円板はメビウスの帯Bになりますが、そのままでは与えられたメビウスの帯Aに密着することはできません。 図は、面が貫通自在なものだとして、密着しようとしているところです。 これができれば、メビウスの帯に円板を貼り合せることできるわけですね。 円板がメビウスの帯に化けているのですから。
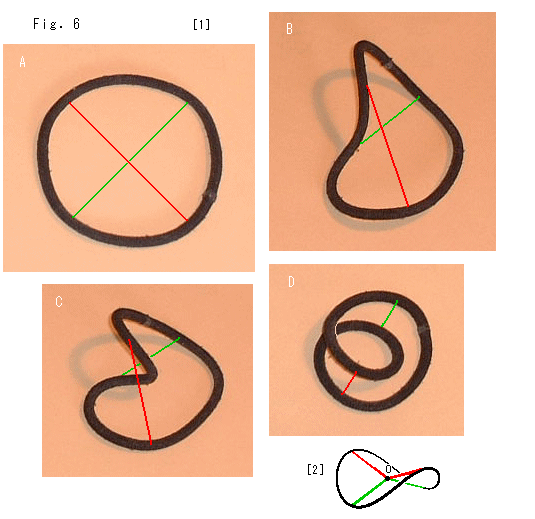
Fig.6をご覧ください。
[1]: 黒いループは女性の髪を束ねる輪です。 これはゴム入りですが、変形した形をほぼ保ちます。 MD対応線に沿って動く円板のフレームを形どってA,B,C,Dと変形します。 面は張ってありませんが、いずれも円板やメビウスの帯であると想ってください。 円板Aはメビウスの帯Dへと変化します。 赤と緑の線は直径です。 それは後からの手描きですが、はじめに黒い輪Aに直径の両端の印しをつけておくとよいでしよう。 むろん、張力が弱くて伸縮性のよい糸があれば、それを使うにこしたことはありません。
この円板は、貫通自在ではないのでFig.5のようなことはできませんが、メビウスの帯になったり円板になったりすることができます。
変形が自由な円板でも、その中心や直径が分離しないふつうの円板では、こうはなりません。 やわらかいゴム板をいじくってみると、不可能なことが直ぐにわかります。 穴がつくれないのです。
[2]: ふつうの円板を歪めた一例です。 赤と緑の直径は、その中点が円の中心Oに固定されているので折れ線になっています。 [1]はMD対応線に沿って動くとしてのものですから、このふつうの円板のような形にしてはなりません。 円板とメビウスの帯が変形し合えるのは、MD対応線に沿った動きに限られるのです。
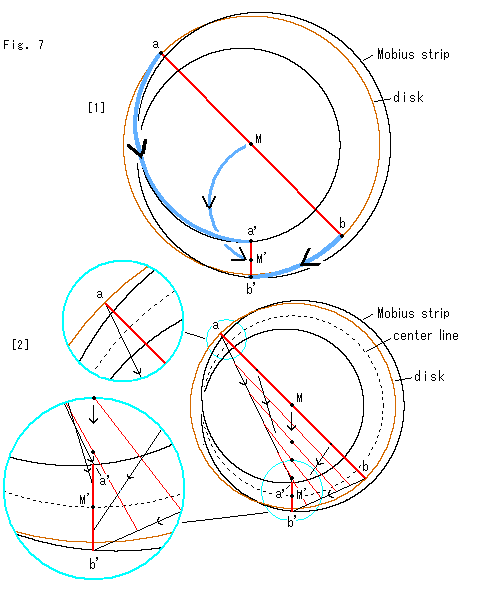
Fig.7をご覧ください。
円板をMD対応線に沿って動かしていくときの、円板の直径の変化の様子をくわしく見てみます。
[1]: 茶色い円は円板(disk)です。 その中心Mに黒い縁のメビウスの帯(Mobius strip)の中心を重ねます。 図は、それを真上から見たものです。 円板がメビウスの帯に変化していくと、円板の直径abはメビウスの帯の向かい合った縁を結ぶ線分a'b'になり、中点(中心)Mは線分a'b'の中点M'になります。 それらの軌跡は青いカーブのように思えますが、そうではありません。
[2]: 実際の移り変わりを順に追っていったものです。 点線は、メビウスの帯のセンターライン(center line)です。 点Mは赤い直径abの中点で、最初の円板の中心です。 左側の水色の2つの円内は、点aや点M'の付近を拡大したものです。
円板がメビウスの帯の方へと近づいていくと、赤い直径ab上の点は矢印のように真直ぐに動いて、両端a,bはa',b'へ、中点MはM'へ移ります。 部分的にコイル状になる動きがあって円板はメビウスの帯に変わります。 それなのに、赤い線の上の点は直線に沿って動きます。 どうしてでしようか。 それは、MD対応線が直線ですからです。
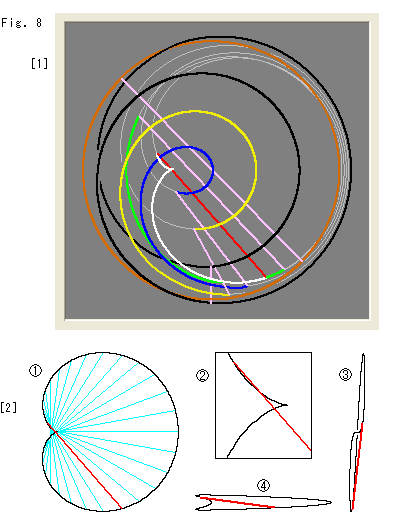
Fig.8をご覧ください。
[1]: 円板からメビウスの帯へと変形していく過程をを真上からコマ撮りして重ねて描いたものです。 赤い線とピンクの線は直径です。 最初の円板を茶色に、最後のメビウスの帯を黒にしています。 それ以外のは、ピンクの直径の左上の端から左回りに右下の端までを図のように色づけしています。 灰色のところは、残余の部分です。
[2]: [1]の白く染めたカーブは、円板に穴が開いてメビウスの帯になろうとするときのものです。 それを細かく見てみます。
 : そのときの円板です。
: そのときの円板です。
 :
:  の白い縁が尖って見えるところを拡大したものです。
の白い縁が尖って見えるところを拡大したものです。
 :
:  を左から見たものです。
を左から見たものです。
 :
:  を水平にして、こちら側(
を水平にして、こちら側( の下側)から見たものです。
の下側)から見たものです。
この[2]は、正面 と真横
と真横 と真上
と真上 の三面図ですから、今まさに穴が開こうとしているところなのか、しかとは見えません。 次で、その臨界付近だけを取り出して、見てみましよう。
の三面図ですから、今まさに穴が開こうとしているところなのか、しかとは見えません。 次で、その臨界付近だけを取り出して、見てみましよう。
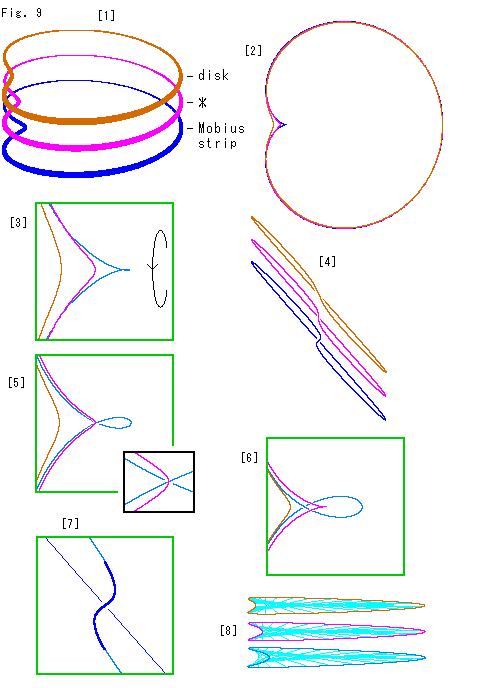 Fig.9をご覧ください。
Fig.9をご覧ください。
歪められた円板とメビウスの帯が、MD対応線の上と下からたがいに近づき合って、ぴったりと一つに密着せんとするところを見ます。 もし密着できたなら、私たちは「メビウスの帯に円板をかぶせることを具体的に実現」したことになるではありませんか!
いや、そんなことができるはずがありません。 密着できたとしても、できたものは、円板が円板でありメビウスの帯がメビウスの帯である状態でくっついていることにならないからです。
そんな密着であるとしても、どのようにそうであるのかを見てみましよう。
[1]: 茶色いフレームは変形した円板です。 青いフレームはメビウスの帯が穴を極度にすぼめてきたところのものです。 そして、ピンクのフレーム(*)が、それらの中間にあります。 それは、無限小の穴をもったメビウスの帯だともいえるし、たんに歪んだ円板だともいえるとします。 この特別なフレームに面を張ったものを補間プレートと名付けておきます。
補間プレートの面は貫通自在でなくてよいのです。 そのことは、あとの実験で確かめます。
[2]: [1]を真上から見たものです。 左端の窪んだところ以外は、3つのフレームがほとんど重なって見えます。
[3]: [2]のフレームの凹んだ付近を拡大したものです。 このままでは青いフレームにあるメビウスの帯の穴が見えないので、それぞれのフレームを矢印のように少し回転します。
[4]: 回転したものを左から見たところです。
[5]: 回転の途中です。 青い線がなめらかになって、メビウスの帯の穴がしっかりと覗けます。 右下の黒い小さな囲みは、青い線がX状になっているところを、さらに拡大したものです。 いま、そのX状のちょうど真上をピンクのフレームが通っていますが、そう見える角度をとったとろなのです。
[6]: さらに回して、穴が最大に見えたところです。 45 くらいずつ傾けたところです。 ピンクの線が尖って見えます。 [4]は、このときのものです。 3つのフレームのS字形になっているところをよく見比べてください。
くらいずつ傾けたところです。 ピンクの線が尖って見えます。 [4]は、このときのものです。 3つのフレームのS字形になっているところをよく見比べてください。
[7]: [4]の青いフレームのS字形になっているところを拡大したものです。 [6]の青い線を左から見たのと同じです。 太く描いてあるところは、[6]で穴として見えている部分で、コイル状になっています。
< [8]: [1]を水平にして、各フレームに面を張ります。 面は、これまで同様に水色の線で表現します。 図は、それをこちら側([2]の画面の下側)から見たものです。 左側の窪んだところに注目してください。 青いフレームに張った面、つまりメビウスの帯の面は、窪みの中に見えます。 しかし、茶色のフレームの面や補間プレートであるピンクのフレームの面は、窪みの中へはまったく回り込んでいません。
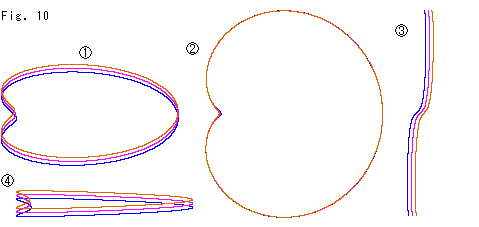
Fig.10をご覧ください。
上のFig.9のピンクのフレームを固定しておいて、上下のフレームをさらに近接させます。
すると のように、3つのフレームは非常によく似た形になります。 上から見た
のように、3つのフレームは非常によく似た形になります。 上から見た では、窪みのところだけは少しずれていますが、そのほかは区別がつきません。
では、窪みのところだけは少しずれていますが、そのほかは区別がつきません。  は
は の左半分を左から見たものです。 3つのフレームのS字形のところが、ほとんど同じ形になっています。
の左半分を左から見たものです。 3つのフレームのS字形のところが、ほとんど同じ形になっています。  は
は を水平にして、こちら側から見たものです。
を水平にして、こちら側から見たものです。
円板とメビウスの帯は、補間プレートに変形すれば、きっちり密着できそうです。 しかし、それはフレームだけを見てのことです。 面が張られていていると、どうでしようか。
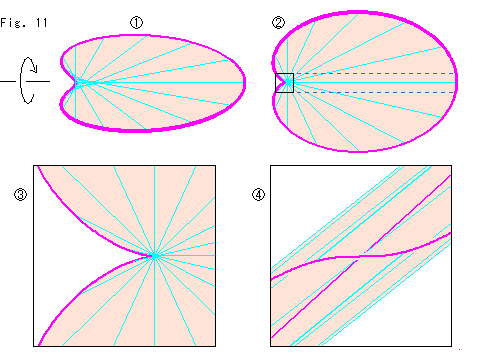 Fig.11をご覧ください。
Fig.11をご覧ください。
補間プレートのフレームに面を張りました。 水色の線は直径です。  では、窪みの付近で面が捩れているように見えるので、こちら側を起こして矢印の方向に回してみます。 すると
では、窪みの付近で面が捩れているように見えるので、こちら側を起こして矢印の方向に回してみます。 すると のように適当なところで、すべての直径の一端が黒く囲んだ窪みの底に集中しているのが見られます。
のように適当なところで、すべての直径の一端が黒く囲んだ窪みの底に集中しているのが見られます。  は
は の黒い囲みを拡大したものです。
の黒い囲みを拡大したものです。  は
は の黒い囲みを含む点線の範囲を左から見て拡大したものです。
の黒い囲みを含む点線の範囲を左から見て拡大したものです。
これらを見ると、面は捩れてはいますが、直径どうしは立体交差していません。 螺旋スベリ台のようになっていると思ってもよさそうですが、うまくいきません。 しいてイメージすると、それは軸と周端の区別がつかないほどに歪んだもので、上り下りの別もないものになってしまいます。 ですから、既知のものに似せて考えることはしないで、ありのまままの形を受け入れてください。
ともかく、2つの補間プレートの面と面は密着できそうですね。
 Fig.12をご覧ください。
Fig.12をご覧ください。
それでは、実験をします。 いまや補間プレートになろうとする直前のものは、補間プレートと同じであるとしてよい。 その補間プレートには無限小の穴があるとしてもよいし無いとしてもよい。 と考えて、同じ2つの補間プレートをつくります。 それらの面は、硬くて貫通できないものでよいのです。 それで、写真のように針金を手芸用のディップ液に漬けて膜を張り、補間プレートを作りました。
[1]: 同じ形の補間プレートです。 観察しやすいように、補間プレートの面の歪みを誇張した形にしています。
[2]: この2つの補間プレートを密着させようとしているところです。 たがいの面を壊すことなく密着できることがわかります。
こんなことは、実験というほどのものではと思われるかもしれません。 しかし、頭の中だけで思考実験的なことをして、絶対に間違いないと言い切れますか。 面と面が妨げあうことなく、スッと触れ合わせたのを実際に目で確かめれば、まさに一目瞭然です。 実験は簡単ですが、思考でこれをするのは容易ではありません。 知恵の輪などで知られるように3次元になると、ふつうの人間は認識力のとぼしいものです。
数学的な面というものを物理的につくることは不可能ですから、何かの物体で実験するのは完全とはいえません。 物と物を密着させると、密着している境界は一つの面になりますが、その面を構成している物理的な厚みのある物と物は、積み重ねた状態になります。 補間プレートを十分細い針金と薄い膜でつくっても、この積み重ねをするほかありません。 ですから、この実験には推測に頼らねばならない限界があるのです。 しかし、これで2つの補間プレートが密着できることが明確にわかりました。
正直にいうと、実験に頼ったのは、補間プレートの面を解析的に表現して解くことが私たちには手に負えないからです。 しかし、そんな計算ができたとしても、それでスッキリするでしようか。 私たちは、数学的な証明よりも、このような実験を好みます。
補間プレートは歪んだ円板でもあり、無限小の穴をもつメビウスの帯でもあるシロモノです。 無限小の穴の開いたものは、穴のまったくないものと同じだとしてもよいと思えます。 しかし、トポロジー的には、穴の開いたものと穴の開いていないものを同じだとすることはできません。
たしかにそうです。 けれども、補間プレートを介して、メビウスの帯とふつうの円板はたがいに移りあうことができます。 いま、それが確かめられたというわけです。
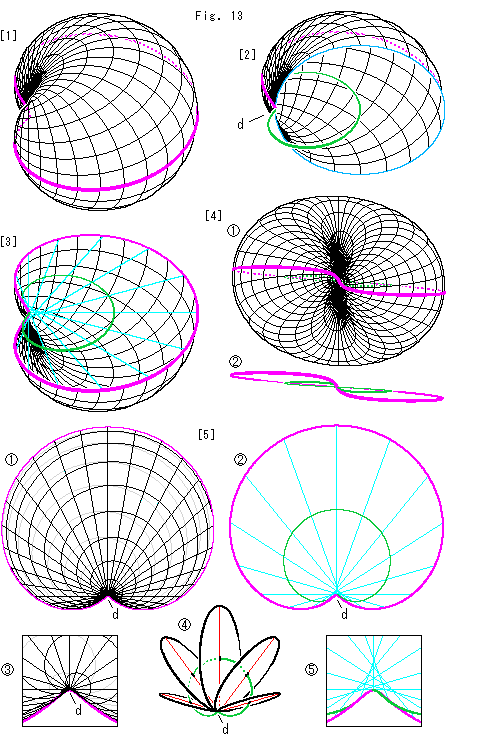 Fig.13をご覧ください。
Fig.13をご覧ください。
メビウスの帯はソリッドトーラスを削って作れるのですから、補間プレートに見合った歪形トーラスとでもよべるものが考えられます。 それを工夫してみます。 地球の経緯線と対比した考えですすめます。
[1]: ピンクの補間プレートを挟んでいる歪形トーラスです。 これは、穴がなくて輪になっていません。 (無限小の穴はある。)
[2]: [1]のこちら側の半分を切り落として、内側を空洞にして覗いたものです。 点dは窪みの底です。 経線と緯線のすべてがこの点dをかなめに通って、補間プレートのフレームのゆがみに合うように描かれています。 フレームは、ゆがんだ赤道です。 点dはこの赤道上にありますが、緯度から見れば北極であり南極でもある点です。 経線は円ですが、その中心は補間プレートの緑色のセンターライン("直径"の中点を連ねてなる曲線)上にとっています。 センターラインがチューブの中心線になっているのです。 地球の経線の中心は1点ですが、歪形トーラスの経線の中心は線状です。
[3]: 歪形トーラスの上半分を補間プレートを残して取り去ったものです。 水色の線は補間プレートの直径で、面を表現しています。 補間プレートの直径は、経線の円の直径ではありません。 その円の中心は緑色のセンターライン上にありますが、円周は点dを通っています。 つぶさに見ていきましよう。
[4]: 窪みのある側を正面として、真正面から見たものです。  はその全体で、緑色のセンターラインを透かし描きしています。
はその全体で、緑色のセンターラインを透かし描きしています。  は補間プレートのフレームとセンターラインだけを取り出したものです。 当然、センターラインもフレームと同様にゆがんでいます。
は補間プレートのフレームとセンターラインだけを取り出したものです。 当然、センターラインもフレームと同様にゆがんでいます。
[5]: [4]を真上から透かして見てみます。
 : 向こう側([4]の下側)を灰色で描いています。 放射状の線は経線で、真上から見てチューブの円の直径と同じです。 つまり、経線の円は、すべて画面に垂直です。 補間プレートの面には垂直ではありません。
: 向こう側([4]の下側)を灰色で描いています。 放射状の線は経線で、真上から見てチューブの円の直径と同じです。 つまり、経線の円は、すべて画面に垂直です。 補間プレートの面には垂直ではありません。
 : 補間プレートの面です。 水色の直径は、[3]と同様に数を減らして捩れが窪み付近にあるのを見やすくしています。 緑色の線はセンターラインです。
: 補間プレートの面です。 水色の直径は、[3]と同様に数を減らして捩れが窪み付近にあるのを見やすくしています。 緑色の線はセンターラインです。
 :
:  の窪み部分を拡大したものです。 すべての経線と緯線がたしかに点dを通っているのが見えます。
の窪み部分を拡大したものです。 すべての経線と緯線がたしかに点dを通っているのが見えます。
 : 補間プレートのセンターラインがチューブの円の中心を通っている様子です。 赤い線は一端を点dとする直径です。 この赤い直径のなす面は、補間プレートの面
: 補間プレートのセンターラインがチューブの円の中心を通っている様子です。 赤い線は一端を点dとする直径です。 この赤い直径のなす面は、補間プレートの面 とは同じではありません。 しかし工作する上では、その差はわずかです。
とは同じではありません。 しかし工作する上では、その差はわずかです。
 :
:  の窪み部分を拡大したものです。 補間プレートの直径は、チューブの円の直径とはちがって、どの端もフレーム上に並んでいます。
の窪み部分を拡大したものです。 補間プレートの直径は、チューブの円の直径とはちがって、どの端もフレーム上に並んでいます。
この歪形トーラスを中身の詰ったものだとします。 その上下を削り落としていけば、補間プレートが得られます。 もっとも、平坦な面ではないので、"直径"に沿って削らねばなりません。
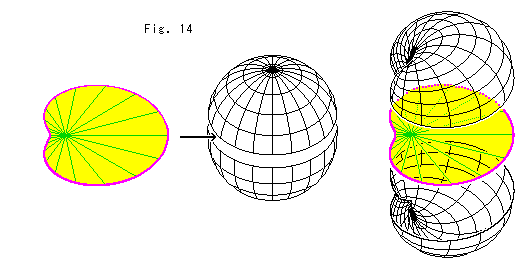 Fig.14をご覧ください。
Fig.14をご覧ください。
MD対応線上の円板からメビウスの帯までの変化にあわせて、歪形トーラスを描くことを考えます。 球とトーラスをMD対応線のような線でむすんで動かすと、球がトーラスになり、トーラスが球になる予想通りの変化が起こります。 ところが、上のFig.13の歪形トーラスが出現しません。 そのため図のように、MD対応線上を動いていく円板を球に差し込んで、その円板の変形に応じて球を歪めていくことにします。 球の歪め具合は、上のFig.13の考え方にならいながら、もっともらしい形にしていきます。 これは、円板そのものを捻じりながら上下に膨らませると想ってもよいでしよう。
このように変形する球とトーラスをむすびつけるMD対応線のようなものを作ろうとして変化をなぞってみると、とても歪んだものになってしまいます。 それで、対応線のようなものは考えずに、円板の変形にしたがって変わる球の姿を見ていくことにします。
下のFig.15をご覧ください。
ここでも、地球の経緯線になぞった言葉を用います。 子午線(経線)とは、半円ではなく大円を指すものとします。 経緯線がどんなに歪んでも、ことばを代えずにおきます。
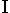
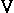 は図の縦の列を表しています。 変化がわかりやすいように、経線だけの図[1] (
は図の縦の列を表しています。 変化がわかりやすいように、経線だけの図[1] (
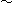
 ) と緯線だけの図[2] (
) と緯線だけの図[2] (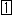
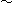
 ) と、それに北極と赤道と南極がどのようになっていくかをスケルトンに描いた図[3] ((1)
) と、それに北極と赤道と南極がどのようになっていくかをスケルトンに描いた図[3] ((1)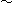 (5)) を並べています。
(5)) を並べています。
一番左の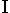 (
( ,
,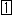 ,(1)) が最初の円板から作ったもので、完全な球になっています。 円板と同様に、この球は、対心点が同一視されるものだとします。 最後の
,(1)) が最初の円板から作ったもので、完全な球になっています。 円板と同様に、この球は、対心点が同一視されるものだとします。 最後の (
( ,
, ,(5)) が形の整ったメビウスの帯から作ったのものです。 そして、中間の
,(5)) が形の整ったメビウスの帯から作ったのものです。 そして、中間の (
( ,
, ,(3)) が補間プレートのもので、Fig.13と同じものです。
,(3)) が補間プレートのもので、Fig.13と同じものです。
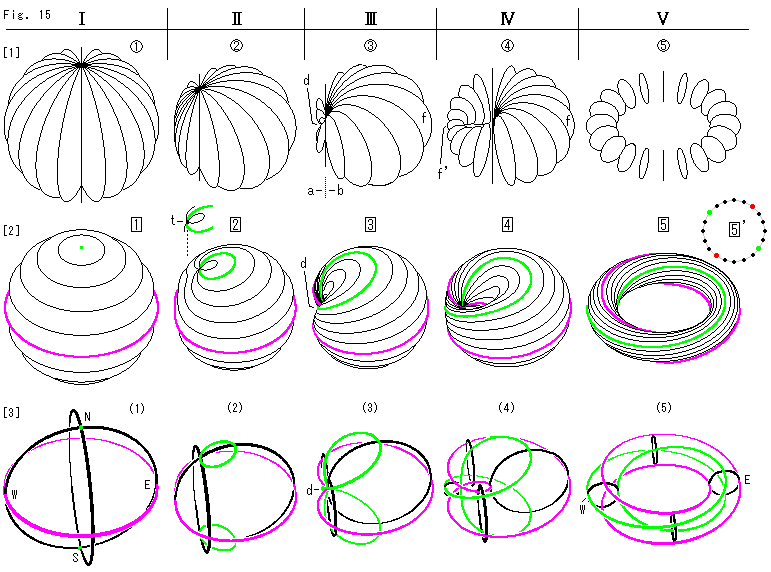
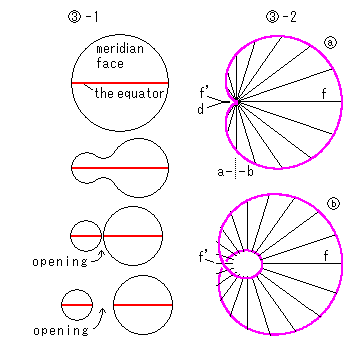 [1]: 子午線を面として描いています。 その面を便宜的に子午面(meridian face)とよんでおきます。 画面に垂直になっている子午面は、真直ぐな線で描かれています。
[1]: 子午線を面として描いています。 その面を便宜的に子午面(meridian face)とよんでおきます。 画面に垂直になっている子午面は、真直ぐな線で描かれています。
 : ここでまとまっている子午線は、
: ここでまとまっている子午線は、 でばらけて、
でばらけて、 になるとトーラスのチューブの断面である小さな円になります。
になるとトーラスのチューブの断面である小さな円になります。
 : 全体がすこし小さいのは、MD対応線の束が途中でちょっと絞られているためです。
: 全体がすこし小さいのは、MD対応線の束が途中でちょっと絞られているためです。  と
と の間では、子午面は完全な円形ではなくて、ひょうたん形
の間では、子午面は完全な円形ではなくて、ひょうたん形 のようになっています。
のようになっています。
 : 補間プレートには(無限小の)穴が開いているものとして描いてあります。 穴が開いても、"円板"である赤道(equator)面の直径の数は変わりません。 しかし、ここでは子午面の数が倍になるのを許すことにします。 そして右の図
: 補間プレートには(無限小の)穴が開いているものとして描いてあります。 穴が開いても、"円板"である赤道(equator)面の直径の数は変わりません。 しかし、ここでは子午面の数が倍になるのを許すことにします。 そして右の図 -1のように、赤い赤道面上にある1つの子午面がくびれて行き、赤道面に穴(opening)が開くやいなや、向かい合った2つの子午面になるとします。 そうしないと、経緯線で面の歪みや伸縮を表現しているので、
-1のように、赤い赤道面上にある1つの子午面がくびれて行き、赤道面に穴(opening)が開くやいなや、向かい合った2つの子午面になるとします。 そうしないと、経緯線で面の歪みや伸縮を表現しているので、 から
から へ来たときに突然、子午面の数が見た目に半減したものになってしまうからです。 (図
へ来たときに突然、子午面の数が見た目に半減したものになってしまうからです。 (図 -1では赤道面の歪みを無視しています。)
-1では赤道面の歪みを無視しています。)
上の では窪みdの奥にある小さい子午面が見えませんが、垂直に描かれている子午面の左側aと右側bには同じ枚数の子午面があります。 真上から見ると、右の図
では窪みdの奥にある小さい子午面が見えませんが、垂直に描かれている子午面の左側aと右側bには同じ枚数の子午面があります。 真上から見ると、右の図 -2の
-2の のようになっています。 子午面fの左端が点dですが、そこに点であるもう1つの子午面f'が重なっているのです。 そうして、すべての子午線が点dを通っています。 その後、穴が広がるにつれ
のようになっています。 子午面fの左端が点dですが、そこに点であるもう1つの子午面f'が重なっているのです。 そうして、すべての子午線が点dを通っています。 その後、穴が広がるにつれ のように子午面がばらけていきます。
のように子午面がばらけていきます。
 : 穴が小さく広がっているのが見えます。 子午面の水平な直径の向きは、Fig.4の"直径"と同じではありません。 形のよいトーラスになることを考慮して、見やすいように、穴の中心を通る直線上に直径を乗せています。
: 穴が小さく広がっているのが見えます。 子午面の水平な直径の向きは、Fig.4の"直径"と同じではありません。 形のよいトーラスになることを考慮して、見やすいように、穴の中心を通る直線上に直径を乗せています。  のときに点であった子午面f'が大きくなって、子午面fと向かい合っています。
のときに点であった子午面f'が大きくなって、子午面fと向かい合っています。
 : 形の整ったト−ラスです。
: 形の整ったト−ラスです。  と同様に、子午面が大きさのそろった円になっています。
と同様に、子午面が大きさのそろった円になっています。
[2]: 緯線も、緯線からなる面として描いています。
 : このときだけ緯線が円形です。 あとは大きく歪んでいきます。 緑色の点は北極で、赤い線は赤道です。 北極はFig.4の円板の中心に相当します。 南極は下に隠れていえ見えませんが、それも円板の中心に相当します。 Fig.4の[3]と見比べていってください。 緯線の数は北極と南極を含めて、
: このときだけ緯線が円形です。 あとは大きく歪んでいきます。 緑色の点は北極で、赤い線は赤道です。 北極はFig.4の円板の中心に相当します。 南極は下に隠れていえ見えませんが、それも円板の中心に相当します。 Fig.4の[3]と見比べていってください。 緯線の数は北極と南極を含めて、 の経線の数と同じにしています。 そうしておくと、トーラス上の経線と緯線の数がそろいます。
の経線の数と同じにしています。 そうしておくと、トーラス上の経線と緯線の数がそろいます。  'はトーラスのチューブを適当なところで切断して見たものです。
'はトーラスのチューブを適当なところで切断して見たものです。
 : 左上の方がすこし窪みはじめているのが見えます。 むろん南半球でも、同様です。 緑色の北極がループに化けています。 ループになっていても、北極とよびつづけます。 その左端tから垂れている点線が子午線の集まっているところです。 しかし、点tを極点とよんだり、点線を地軸とぶわけにはいきません。 なぜなら、赤道から緯線をかぞえていくと、緑色のループのところが北極に相当するからです。 私たちの北極は点でがなくて、緑色のループ全体です。
: 左上の方がすこし窪みはじめているのが見えます。 むろん南半球でも、同様です。 緑色の北極がループに化けています。 ループになっていても、北極とよびつづけます。 その左端tから垂れている点線が子午線の集まっているところです。 しかし、点tを極点とよんだり、点線を地軸とぶわけにはいきません。 なぜなら、赤道から緯線をかぞえていくと、緑色のループのところが北極に相当するからです。 私たちの北極は点でがなくて、緑色のループ全体です。
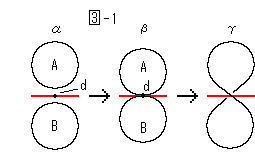
 : 点dは窪みの底なので図では見えませんが、経線と同様にすべての緯線がその点dを通ります。 ループになっている北極と南極も点dで継ながります。 つまり、いま全曲線がこの1点dを通っているわけです。 南北両半球の同緯度の緯線どうしのループがペアになって、右の図
: 点dは窪みの底なので図では見えませんが、経線と同様にすべての緯線がその点dを通ります。 ループになっている北極と南極も点dで継ながります。 つまり、いま全曲線がこの1点dを通っているわけです。 南北両半球の同緯度の緯線どうしのループがペアになって、右の図 -1のように変化します。 ループを円で表現しています。 赤い横線は赤道面を、歪みを無視して描き入れたものです。 すべての緯線のペアが、
-1のように変化します。 ループを円で表現しています。 赤い横線は赤道面を、歪みを無視して描き入れたものです。 すべての緯線のペアが、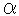 から
から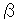 になって点dを共有します。 その後すぐ、
になって点dを共有します。 その後すぐ、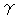 のように8字状の歪んだ1つずつのループになります。
のように8字状の歪んだ1つずつのループになります。
ここでの様子は、 の子午面の場合とちょうど逆です。 左から
の子午面の場合とちょうど逆です。 左から ,
, ときた子午線は、
ときた子午線は、 でばらけはじめます。 緯線の場合は、左から来た別個のループであったものが、この
でばらけはじめます。 緯線の場合は、左から来た別個のループであったものが、この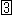 でペアを組んで1つのループになります。
でペアを組んで1つのループになります。
 : 緯線からなる面が捩れているのが見られます。
: 緯線からなる面が捩れているのが見られます。
 : すべての緯線が一斉に流れて、ト―ラスを形成しています。 その流線は捩れています。 緑色の曲線は、ループになった北極と南極が継ながったものです。 赤い曲線は赤道であったものです。
: すべての緯線が一斉に流れて、ト―ラスを形成しています。 その流線は捩れています。 緑色の曲線は、ループになった北極と南極が継ながったものです。 赤い曲線は赤道であったものです。
球の中心は北極と南極の中点を連ねたものであって子午面の中心ですから、描いてはありませんが、トーラスのチューブの中心線(芯)になっています。
[3]: 球の子午線を2つだけにして、それと赤道と北極と南極とから経緯線の変化を見てみます。 (1)のN,E,W,Sは対心点です。 (3)では子午線が足りないように見えますが、1つが窪みdのところで点になっているためです。
(5)を見ると、点E,Wは(1)の対心点と呼応していますが、北極と南極であった対心点N,Sの移った先は点ではなくて、緑色のメビウスの帯の縁になっています。
(1)から(5)へと見渡すと、(4),(5)間は1対1の対応が維持されていますが、他はどの段階でも1対1対応になっていません。 そうです。 この歪形トーラスは、そんなことを気にせずに、もっともらしく捏(コ)ねたものです。
ずっと上のFig.4へ戻ります。
そこでの状況をもう一度見てみます。(インターネット画面をもう一つ出して並べ、見ていってください。)  を境にして見ると、上側(
を境にして見ると、上側( 〜
〜 )と下側(
)と下側( 〜
〜 )の2つのグループは同相ではありません。
)の2つのグループは同相ではありません。  では、その上下との1対1の対応が破れています。 しかし、そこを経る変化は実効的な連続変形です。 そして、
では、その上下との1対1の対応が破れています。 しかし、そこを経る変化は実効的な連続変形です。 そして、 から
から までの上下を支障なく行き来できます。 穴が自然に開閉されるのです。
までの上下を支障なく行き来できます。 穴が自然に開閉されるのです。
トポロジストたちは、トポロジー的に同じものとそうでないものをホモトピーとかイソトピーとかがどうのといって表現しています。 しかし私たちには、そんな用語はどうでもよいのです。 穴の開いたものと穴のないものは同じではないというのなら、それでもかまいません。 補間プレート は往来自由な国境の町のようなものです。 そこを通れば、円板でもメビウスの帯でも、彼らのいう違うものになることができるのですから。 球とトーラスも似た境遇です。
は往来自由な国境の町のようなものです。 そこを通れば、円板でもメビウスの帯でも、彼らのいう違うものになることができるのですから。 球とトーラスも似た境遇です。
[前章] [次章] [目次]
 Fig.1をご覧ください。
Fig.1をご覧ください。

 Fig.4をご覧ください。
Fig.4をご覧ください。 Fig.5をご覧ください。
Fig.5をご覧ください。


 Fig.9をご覧ください。
Fig.9をご覧ください。
 Fig.11をご覧ください。
Fig.11をご覧ください。 Fig.12をご覧ください。
Fig.12をご覧ください。 Fig.13をご覧ください。
Fig.13をご覧ください。 Fig.14をご覧ください。
Fig.14をご覧ください。
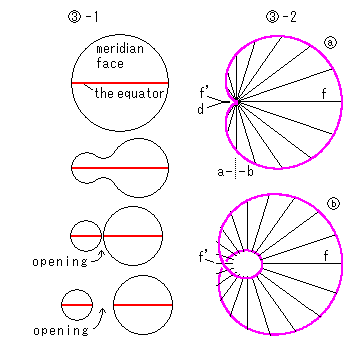 [1]: 子午線を面として描いています。 その面を便宜的に子午面(meridian face)とよんでおきます。 画面に垂直になっている子午面は、真直ぐな線で描かれています。
[1]: 子午線を面として描いています。 その面を便宜的に子午面(meridian face)とよんでおきます。 画面に垂直になっている子午面は、真直ぐな線で描かれています。