第３部 射影幾何から双曲幾何へ
Ch.42 クロスキャップ (3) 
円形の射影平面から無数のメビウスの帯を取り出して、もう一つのクロスキャップを造ります。 それを使うと、クロスキャップと、それを分解したメビウスの帯と円板の三者の関係が見て取りやすくなり、それらの上に具体的な図を描くことができます。
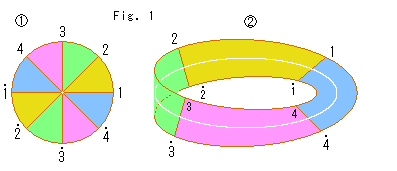Fig.1をご覧ください。
私たちの移りあえるメビウスの帯と円板において、円板上のどの部分がメビウスの帯のどこに移るかを見ておきます。
: 円板を4つの直径で8等分して、色分けします。 中心の1点だけは色分けできないので、白抜きにしておきます。 そして、図のように番号をつけてます。
: 円板がメビウスの帯になったところです。 円板の中心がセンターラインになっています。 点が線になっているのです。 そこ以外の点は、1対1で対応しています。
このセンターラインの対応については、順次考えていきます。
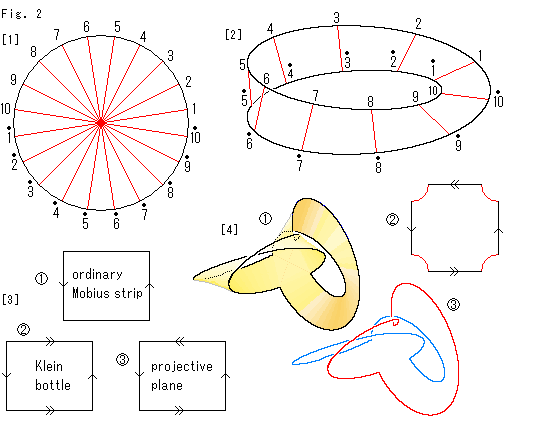Fig.2をご覧ください。
[1]: 対心点を同一視した円板、つまり円形に描いた射影平面です。 円板型射影平面とよんでおきます。
[2]: これまでのことから、円板の縁とメビウスの帯の縁は、図のように対応づけできます。 しかし、このメビウスの帯の向かい合った縁を同一視したものは、射影平面ではありません。 それは、あの内側も外側もないクラインの壷とよばれている曲面です。
[3]: 矢印付き四角形で表すと、ふつうのメビウスの帯(ordinary Mobius strip)はのようになり、クラインの壷(Klein bottle)はのようになります。 そして、射影平面(projective planw)は
のようになります。
[4]: 射影平面でも部分的になら、2つのメビウスの帯を十字につなぐことで簡単にできます。 この図は前にも描いたものです。 しかし、そのときは巾の広いものの代用としてでした。 ここでの考え方は、それとはちょっと違います。 向かい合った縁を捩じて同一視したメビウスの帯があって、その同一視を部分的に実行したものです。 この背中合わせのメビウスの帯の黒い縁を縫い合わせることができればよいのですが、むろん不可能です。 代わりに、矢印つき四角形を真似て描いてみると、のように四隅の欠けた四角形になります。 隅の赤い線は、どことも貼り合わせることができません。 ふつうのメビウスの帯の縁の線は1つのループですが、十字形のこの帯の縁は、のように色分けすることができて、2つのループからなっています。
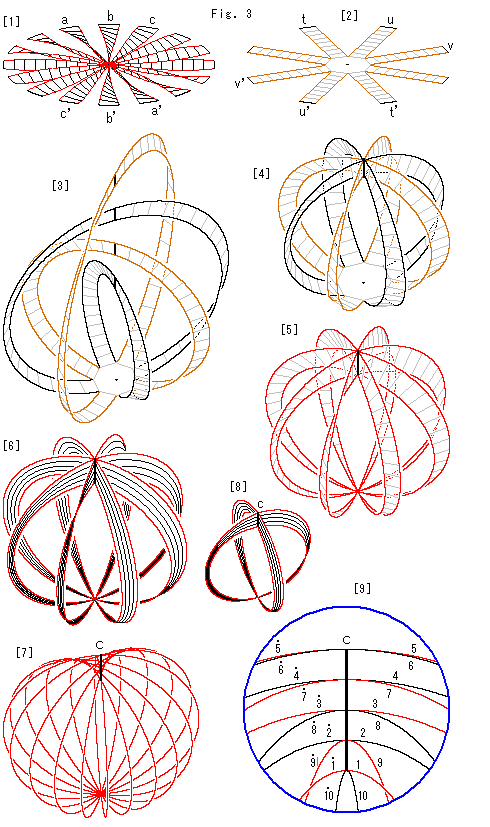Fig.3をご覧ください。
新しいクロスキャップをつくります。
[1]: 円板型射影平面の対心点の同一視を、円板のままで同一視しておくのではなく、物理的に実行しようとします。
図は、円板を扇形にきざんで捻じてみたところです。 このまま個々のプロペラ状の両端aとa', bとb', cとc',,, を継いでいけばよいのですが、見やすく描けそうにはありません。
[2]: そこで一旦、中心の周りを八角形に残して、短冊状に切って広げます。 短冊の縁を赤くしてないのは、迂回工作の気持ちです。
[3]: 各短冊の両端tとt', uとu', vとv',,, を捻じて継ぎ、メビウスの帯にしていきます。 メビウスの帯の捻れの方向はそろえておきます。 黒いきざみ線は継ぎ目です。 タコ足のようですね。 一つおきに足の色を変えてあるのは、見やすくするためです。
[4]: 各メビウスの帯の継ぎ目は貫通自在だとして、そこで交差させます。
[5]: 八角形のところを1点に絞ったものです。 こうすると、[1]の対心点の同一視を実行したものになります。 メビウスの帯の縁を赤く描いてあるのは、縁が円板型射影平面の直径であることを表すためです。
[6]: 各メビウスの帯を黒い線のように細く切ります。 無限に細く切って、メビウスの帯を円板型射影平面の直径にしてしまいます。 もちろん、こんなことは思考的にしかできませんが、それができたとします。
[7]: できた直径を粗くえらんで描いたものです。 線分cはメビウスの帯の継ぎ目であったところですが、いまはクロスキャップの自己交差の交線と同じものになっているはずです。 つまり、このリンゴのように見えるものはクロスキャップになっていると思われます。
[8]: 対心点である個々の直径の端点は、線分c上で継がっています。 しかし、その対心点は自己交差の交線上の点として並んでいなければなりません。
はじめに、[1]を見てメビウスの帯は多いほうがよいと思ったのですが、2つにすれば都合よくいきます。 それは、半球面からクロスキャップをつくったときのことを思い浮かべれば、容易にうなずけます。 図は、2つのメビウスの帯からなる[6]に代わるものです。 Fig.2の[3]の十字形メビウスの帯を、背中合わせでなく、同じ側へもってきたものでよいわけですね。 このようなもので[7]のリンゴをつくります。
[9]: [8]からつくったリンゴ[7]を真直ぐに立てて、線分cの付近を拡大したものです。 番号は、Fig.2の円板型射影平面と同じにとっています。 見やすいように、奇数番号の線を赤に、偶数番号の線を黒にしています。 これで見ると、ドットのない番号の線とドットの付いた番号の線が線分c上でちゃんと継ながっていて、上下の順もうまく整えられています。
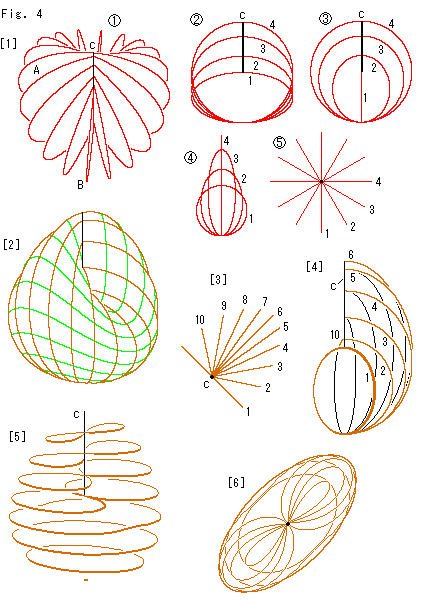Fig.4をご覧ください。
上のリンゴをクロスキャップに仕立てます。
[1]: リンゴの面は、回転楕円面の一種です。 回転軸は線分cを延長したものです。 そしてリンゴの面は、回転とともに回転軸上の半径が変わる楕円の周からなっています。
: 上のリンゴをスケルトンにしないで、こちらへ傾けてみたものです。 Aが最大の楕円で、Bが最小の楕円です。 黒い線分cは回転軸です。 見やすいように、長さを大きくとっています。
: このを作るために、まず、水平半径が同じで垂直半径が異なる楕円を1,2,3, , , のように沢山用意して、下端をそろえて並べます。
: 最大の楕円4(のA)は動かさずに、最小の楕円1を90
回転します。 楕円1は画面に垂直になります。 最大と最小の楕円の間へ残りの楕円を大きさ順に回転します。 図は、そのように各楕円を回転したところです。 に相当しています。
: を真横から見たものです。
: を真上から見たものです。
[2]: 楕円の数を無数に多くすると、クロスキャップらしいクロスキャップになります。 全体の縦横高さの比は適当にとっています。 茶色い線が楕円の縁です。 緑色の線は、楕円の中心角を等間隔にとった点を辿ったものです。 その形は鞍形の縁のようになっています。 茶色い線を経線、緑色の線を緯線と見立てて、そのように呼ぶことにします。
[3]: [2]の右半分にある楕円を真上から見たものです。 最小の楕円が1で、最大の楕円が6です。
[4]: [2]のままで、その右半分を透かして見たものです。 緑色の線は省いてます。 楕円が、その縦軸の大きさを変えながら回転している様子が見て取れます。
[5]: 念のために、水平にきざんで断面を見ると、8字形のところがあります。 ちゃんとしたクロスキャップです。 射影平面である円板の周が線分cであり、それが自己交差の交線になっています。
[6]: [5]を真上から見たものです。 [5]では自己交差の交線cを軸にして全体がすこし捻られているようにも見えますが、そうでないことがこれでわかります。 すなおな形です。
こうしてクロスキャップをつくったのですが、その結果だけを見たのでは、これまでのものとさほど変わり映えしませんね。 しかし、形だけを真似て造ったものではないのです。 ですから、円板型射影平面から自然に得られたものだといってよいでしよう。
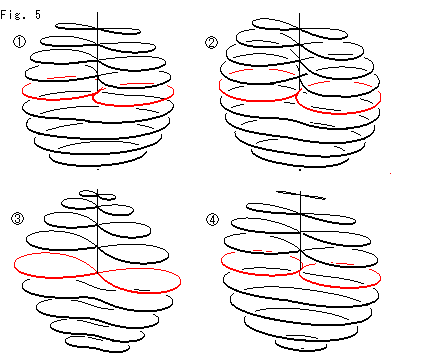
Fig.5をご覧ください。
上のクロスキャップをこれまでに作ったものと並べてみました。 いずれも水平な断面を等間隔に積み上げたスケルトンにして、向きと大きさをほぼ揃え、断面の数を同じにしています。 赤い線は自己交差の交線の下端を切っている断面です。 が新しいクロスキャップです。 は半球面から作ったもので、はカッシ−ニの卵形を利用したもの、はトーラスを変形したものです。 いずれも、クロスキャップとしては本質的な差はありません。
けれども私たちにとっては、新しいクロスキャップが重宝です。 それは、クロスキャップ上の点を簡単に表せて、円板型射影平面などとの関係を一番理解しやすいからです。 それで今後は、この新しいクロスキャップをつかっていくことにします。
(クロスキャップを表す数式がものの本などでいくつか見受けられますが、私たちが試したところでは、どれも作図にすら役立ちませんでした。)
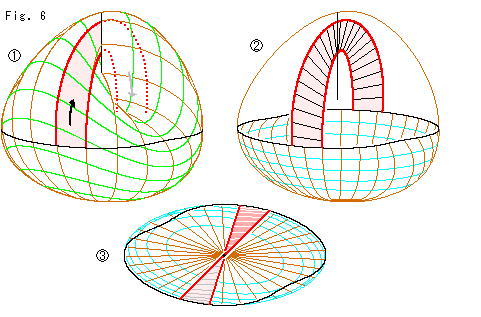
Fig.6をご覧ください。
クロスキャップの面をの赤い帯のように自己交差の交線を通って向こう側まで辿ります。 見やすいように、黒い線から上の余分なところを取り除くと、のようになっています。 手提げかごに似ていますね。 そのハンドルをよく見ると、同じ側だけが見えていますけれど、捩れています。 真上から見ると、のように捩れているのがはっきりわかります。
前に自己交差の交線のところを水平に切った8字形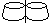
を調べました。 いま、ここでのようにして見てみると、クロスキャップがメビウスの帯と同じ性質の面であることが、より鮮明にわかります。 Fig.3の[5]と見比べてください。
Fig.7をご覧ください。
それでは、クロスキャップ上の点が円板型射影平面上の点とどのように対応しているかを見ていきます。 ここでは便宜的な用語、経線と緯線をつかっていきます。 原点を定めて経線と緯線をどのようにとるかの約束をすれば、どんな2つの曲面の間の対応づけもできるはずです。 対応点を色分けした大きなスポットで表します。
[1]: 円板型射影平面です。 茶色い直径が10本描かれています。 同心円は、緑色のと黒い円周を含めて、10個描かれています。 対心点が同一視されているので、その円周上には同色のスポットが2つずつあります。 緑色のスポットは、番号で識別します。 黒いスポットは中心です。
[2]: クロスキャップです。 自己交差の交線を真直ぐに立て、最小のだ円のフレームを画面に垂直な位置に置いています。 茶色い経線と緑色の緯線は、それぞれ円板型射影平面の直径と緑色の同心円に対応しています。 緑色の線の数が減ったように見えますが、変わってはいません。 濃い緑のスポット6,7,8は、クロスキャップの向こう側の陰になっています。
黒い自己交差の交線は、円板型射影平面の黒い円周に対応しています。 点bと点dは重ねて描かれていますが、1つの点になっているのではありません。 円板型射影平面の円周上の点は対心点ですから、実際の点(スポット)の数は描かれてある数の半分です。 ですから、円板型射影平面上の点とクロスキャップ上の点は、完全な1対1の対応になっています。
[3]: 点bと点dの様子を見るために、自己交差の交線を無理に矢印のように裂いたものです。 a,b,c,dのそれぞれは同一視した後の1個の点です。
図では、円板型射影平面の左右の赤いスポットが自己交差の交線の上端にきていますが、どの対心点をそこへもってきてもかまいません。 それに連れて、クロスキャップ上の対応する点が移動するだけです。
[4]: 円板型射影平面とクロスキャップの対応関係をチャートにしたものです。
[5]: クロスキャップを真上から見たところです。 Fig.4の[6]とは違います。 それは透視等高線でした。 この[5]は、クロスキャップ[2]をそのまま透かして上から見たものです。 緑色の緯線は鞍形の縁のように波打っていますが、真上から見みると、このようになっているのです。
[6]: クロスキャップ[2]を自己交差の交線に沿って画面に垂直に切ります。 この図は、その右半分を斜めから見て、緯線だけのスケルトンにしたものです。 黒い点は切口にある切った緯線の端です。
[7]: クロスキャップを真左横から見たところです。 自己交差の交線は、その上端の赤い点だけが見えています。 内部に隠れている点b,c,dは点線で描かれています。
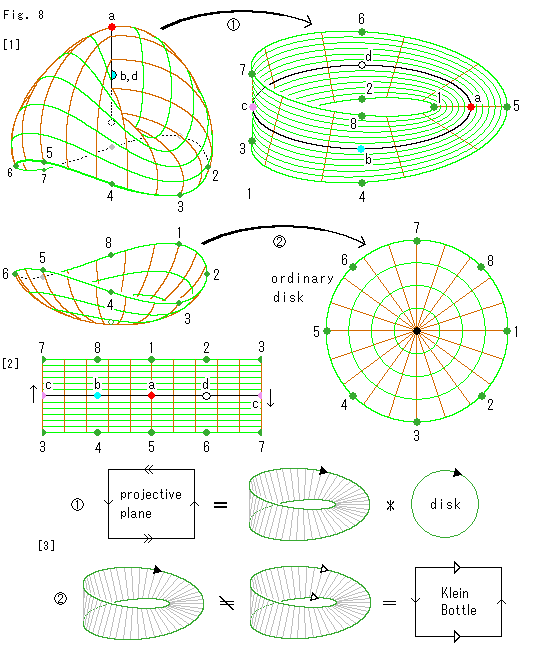Fig.8をご覧ください。
射影平面は、メビウスの帯と円板の縁と縁を貼り合わせたものだといわれています。 それについては色いろと見ましたが、上でクロスキャップと円板型射影平面の対応関係を具体的につかめたので、それを利用して再考します。
[1]: クロスキャップを上下に切り離します。
: メビウスの帯のセンターラインをクロスキャップの自己交差の交線に対応するものとして、対応点を印していったものです。 センターラインだけは1周して閉じるので、好都合です。 Fig.7の[3]を見てください。
この黒いセンターラインは、横切ると何かを生じさせるといったものではなくて、その位置を表しているだけです。 点bと点dは、他の点をそのままにしておいて、交換してもかまいません。
このメビウスの帯は、これまでのようにクロスキャップを変形したり手術したりしたものではありません。 ふつうのメビウスの帯を用意しておいて、それに対応点を印していったものです。 結果は同じですが、考え方が違っています。
: 下部はそのまま広げて円板にします。 これは、ふつうの円板(ordinary disk)です。
[2]: メビウスの帯を短冊に切り開いたものです。
[3]: さて、メビウスの帯と円板を貼り合わせるのですが、濃い緑の対応点同士のすべてをくっつけることは不可能です。 私たちは、「貼り合わせる」ということばを動詞として感じとっていたために、あれこれと空想することを強いられました。 ここでは、メビウスの帯も短冊も動かしません。 変形も切ったり貼ったりもしないのです。 貼るとか、くっつけるといったことはしないで、たんに点と点が対応している(同じ点である)と考えるのです。 それを式の絵にしたのがです。 射影平面(projective plane)は、メビウスの帯と円板からなっていて、両者の縁と縁が対応づけられているということを語っています。 符号*は、その対応を表しています。 黒い矢印は、同一視のマークでもありますが、縁の点が対応づけられていることを表現しています。 ただし、このメビウスの帯自身の向かい合った縁と縁は、同一視するものではありません。 そんなことをすれば、クラインの壷(Klein Bottle)になってしまいます。は、メビウスの帯自身の向かい合った縁と縁を同一視したものはクラインの壷であって、のメビウスの帯ではないことを表現しています。
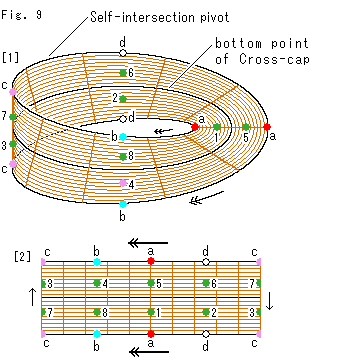
Fig.9をご覧ください。
原点(クロスキャップの底)を円板の中心である1点にとりましたが、ものはためしと、メビウスの帯のセンターラインを原点と同じに扱ってみます。 無謀を承知で、点を線だとするのです。 そして、円板を省きます。
[1]: このメビウスの帯のセンターラインは、クロスキャップの底の点(bottom point of Crosscap)を線にしたものです。 そして、帯の縁をクロスキャップの自己交差の交線(Self-intersection pivot)にとっています。 そうすると、メビウスの帯のセンターラインとクロスキャップの底の点だけを除けば、クロスキャップ上のすべての点をメビウスの帯の上に対応づけることができます。
しかし、その自己交差の交線上の点の同一視は実行されていません。 そのために、同一視の矢印を添えています。 つまり、このメビウスの帯は、射影平面ではありません。 先にいったクラインの壷で、センターラインを円板型射影平面の中心と見立てたものす。 ですけれども、なにかの役立つような気がしないでもありません。 一応の対応付けができるのですから。 それで、仮にMK型射影平面とよんでおきます。
[2]: [1]を短冊にしたものです。 これにも上下に矢印を付けています。
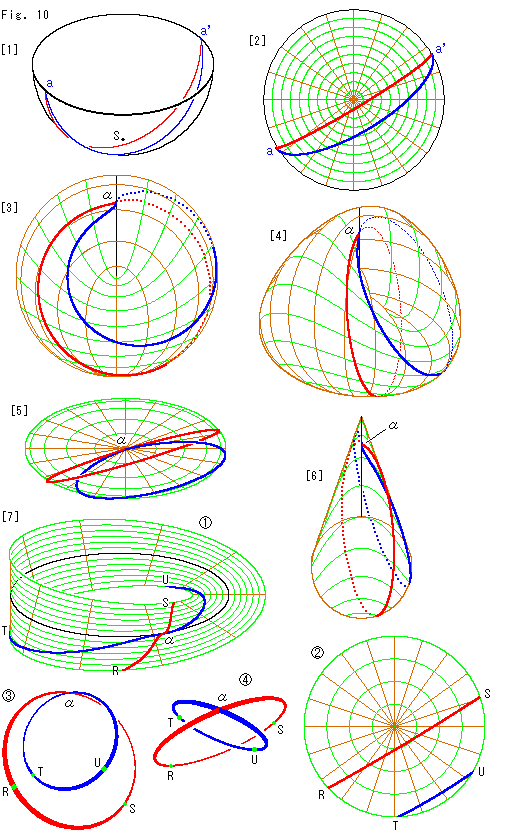
Fig.10をご覧ください。
クロスキャップ上の点と他の形の射影平面上の点の対応がつかめたので、いくつかの曲線を描いてみます。 まず、平行線です。
[1]: 赤と青の曲線aa'は、対心点を同一視した半球面上の平行線です。 点Sは南極です。
[2]: 円板型射影平面です。 その上の平行線は、[1]を真上から見たものになります。 いま点aから出発したとします。 すると、点a'に達するや出発点のaに現れて、ふたたび点a'へ向かいます。 そして、際限なく a - a'- a - a' --- とめぐります。
[3]: 平行線をクロスキャップ上で見たものです。 目で見た端点a,a'が自己交差の交線上の点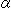
で継がっています。 点線は、向こう側の様子です。
[4]: ななめ横からクロスキャップを見たところです。
[5]: 真上からクロスキャップを見たものです。
[6]: [3]を真左横から見たものです。
[7]: 射影平面(クロスキャップ、円板型射影平面)をメビウスの帯と円板に分解します。
分解したメビウスの帯で見ると、クロスキャップの自己交差の交線であったセンターライン上で平行線が交わっているのがはっきりと見えます。
メビウスの帯上で点R,Tから出発して点S,Uにくると、分解した円板上の点S,Uにジャンップます。 円板上で点R,Tにくるとまたジャンップして、メビウスの帯上の点R,Tにもどって、同じことをいつまでも繰り返します。
ここで面白いことに気付きます。 青い線と赤い線はメビウスの帯上でたしかに交差しているのに、円板上に戻ってきても両者の道は交換されていません。 それは、射影平面がふつうの平面ではない証拠です。
メビウスの帯と円板を具体的に貼り合せることはできませんが、赤と青の曲線だけを取り出して継いでみると、のようになっています。 は、の点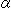のところをこちらへ向けて見たものです。 これがクロスキャップ上の平行線だというわけです。
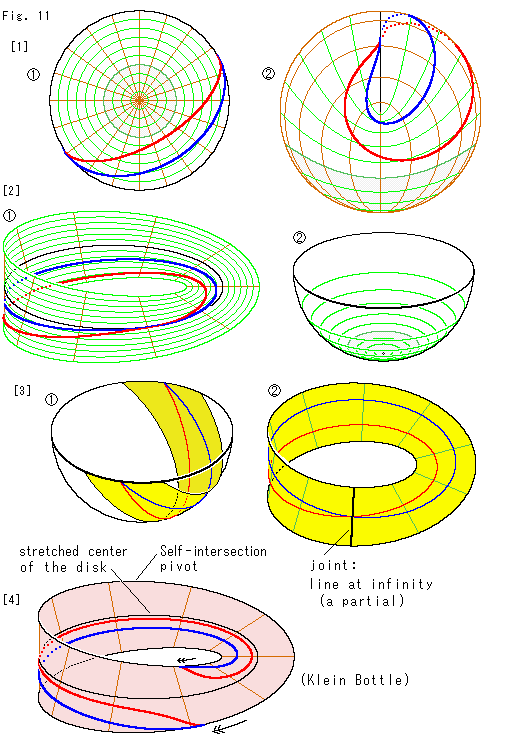Fig.11をご覧ください。
メビウスの帯と円板に分解した場合、曲線が分断されます。 それを避けるために円板を小さくすることが考えられます。 もっとも、円板の中心を通る曲線は例外としてです。
[1]: は円板型射影平面上の平行線です。 灰色のところは、メビウスの帯と円板に分解するときの円板に対応する領域です。 平行線が、その外側を通っています。 クロスキャップ上で見ると、のようになっています。
[2]: メビウスの帯上に平行線を移したところです。 このメビウスの帯は、[1]でいえば、円板型射影平面から灰色の円板を取り去った跡であり、クロスキャップから灰色の椀状の下部切り取った残りです。 は、半球面での円板の位置を覗いてみたものです。 灰色部分が円板です。 緑色の緯線は、[1]のそれに対応して描かれています。 底にあるその円板をくり抜いてから、対心点を同一視すれば、メビウスの帯が得られます。
このメビウスの帯は射影平面全体ではありませんが、そこに平行線の全貌を見ることができます。 このように円板がなくても事が足りる場合があるのです。 そこで、円板を使わなくてすむときのメビウスの帯をメビウス型射影平面と名づけて、活用していくことにします。
[3]: これまでにたびたび作ったメビウスの帯でも、縁から逸れていかない平行線なら、その全体を見ることができました。 それは、のように平行線を含んだ黄色い帯を切り取ってつくったものでした。 このメビウスの帯と、いま名づけたメビウス型射影平面との違いを見てみます。
メビウス型射影平面のセンターラインはクロスキャップの自己交差の交線に対応するもので、その自己交差の交線は半球の縁全体でした。 半球の縁は無限遠直線(line at infinity)です。 つまり、メビウス型射影平面のセンターラインは無限遠直線の全体です。 黄色いメビウスの帯では継ぎ目(joint)が半球の縁(無限遠直線)です。 しかし、それは無限遠直線の一部分(a partial)でしかありません。 メビウス型射影平面が無限遠直線全体を含んでいるというのは、大きな利点です。
黄色いメビウスの帯の継ぎ目の方向と、緑色のメビウス型射影平面のセンターラインの伸びている方向は、1直角ほどもちがいます。 そして、黄色いメビウスの帯の縁と縁をむすんでいる緑色の線分は、円板型射影平面の直径にではなく、緯線に対応しています。 ですから、これらのメビウスの帯の面は、全体としてではありませんが、たてよこが交換されているいるわけです。
[4]: こころみに、MK型射影平面に平行線を描いたものです。 ふつうのメビウスの帯ではないので、帯の地色を他のと違えています。 図の stretched center of the disk (円板の引き伸ばした中心)がセンターラインです。 このメビウスの帯の縁である自己交差の交線は、同一視を実行する前のものです。 様子がメビウス型射影平面上とは逆になっていますね。 絵としては、[2]のセンターラインと縁を交換したものが、[4]になっています。 しかし、見た目にそのように見えますが、メビウスの帯[2]の縁は分解した円板の中心ではありません。
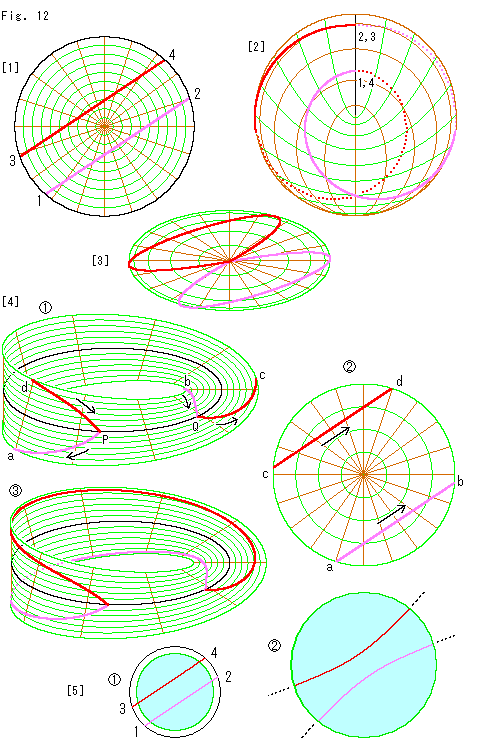
Fig.12をご覧ください。
[1]: 円板型射影平面上に見た目に真直ぐな1本の線を引いてみたものです。 1 - 2 - 3 - 4 - 1 - 2 - - - と巡る1本の曲線ですが、どこがどこだかわかるように赤とピンクに色分けしています。
[2]: 曲線をクロスキャップ上に移したものです。 点線は、自己交差の交線を横切って向こう側を巡っているところです。
[3]: 真上から見たクロスキャップ上の曲線です。 曲線は際限なく同じ8の字を描いて伸びています。
[4]: とは、射影平面[1]をメビウスの帯と円板上に分解したものです。 はメビウス型射影平面です。 上の曲線が図のようになっています。
とで見てみます。 メビウスの帯のセンターライン(自己交差の交線)上の点Pから点aへ向かって出発したとすると、
P - a - (a - b) - b - Q - c - (c - d) - d - P - - -
のように,の間をジャンプしながら、ぐるぐる回りつづけます。 括弧()の中は円板上です。
のメビウス型射影平面では、曲線が一続きのループになります。
いずれの場合も、センターラインを2箇所で横切っています。 これは、目で見て真直ぐな線は射影平面上の直線ではないからです。
それにしても、メビウス型射影平面上の点Pや点Qのところで曲線が鋭く折り返されていますね。 それは、[1]で2から3へ移るときに、実際は曲線が折れているからです。 半球面上の大円が射影平面上の直線ですから、そのように(見た目に)カーブした曲線なら、センターラインを1箇所でなめらかに横切るのです。 Fig.10,11を見てください。
[5]: それでは逆に、円板型射影平面上で見た目に真直ぐな線となるもとのユークリッド平面上の曲線は、どんなのでしようか。 は円板型射影平面を小さく描いたものです。 その周は無限遠直線ですので、そこにある曲線をそのまままユークリッド平面に移すことはできません。 水色に染めてあるところは、実際に移す範囲を限ったものです。 そこを取って、ユークリッド平面に移したのがです。 かなり大きくなっています。 そして予想どおり、曲線が内側へ曲がっています。 そうです。 双曲線になっているのです。 最初のCh.1を見てください。
(私たちの双曲幾何でもこのようなことをしたいのですが、それは不可能です。 けれども、おいおい工夫していきます。)
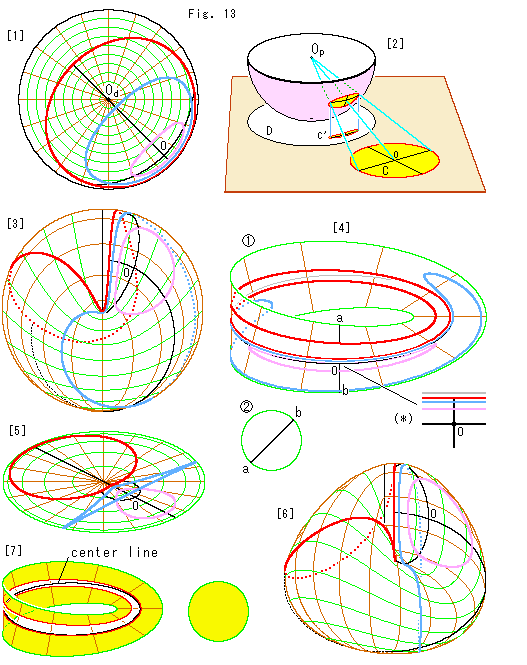Fig.13をご覧ください。
円だとどうなるでしようか。
[1]: 円板型射影平面上に同心円Oを描きました。 黒い線は直交する2つの直径で、その1つは円板型射影平面の中心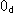
を通っています。
[2]: どのようにして円板型射影平面上に円を描いたかの説明図です。 白い円板Dが円板型射影平面で、赤色い縁の円Cがふつうの円です。 両者は同じ茶色の平面上にあります。 円Cを図のようにピンクの半球面を経由して円板D上に移します。 点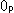
は半球の中心です。 円Cは点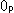を中心とする中心射影で半球面上に移され、そこから円板D上に正射影されて円C'となります。 このようになっているので、[1]の曲線はふつうの同心円らしくは見えませんが、射影平面上の同心円です。
この射影の図からすぐ気づくことは、もとの赤色い縁の円Cをどんなに大きくしても、円板型射影平面D上に移された円C'はけっして円Dの円周に触れることはないということです。 円Cを無限大にしたときにかぎって、円C'は円Dの円周になります。 しかし、どんな場合でも、円Cが円Dの縁を越えることはありません。
[3]: クロスキャップ上に同心円Oを移したものです。 点線は向こう側を這っているところです。 たしかに、どの円も自己交差の交線を横切っていません。 それにしても、この図だけを見て、同心円だと認識することは至難ですね。
[4]: クロスキャップをメビウスの帯と円板に同心円とともに分解したものです。 円を小さくとっているので、同心円の円が3つともメビウスの帯
上にあります。 緯線は省いてあります。 灰色の曲線はセンターライン(=クロスキャップの自己交差の交線)です。 右下の(*)は同心円の中心Oの付近を拡大したものです。
メビウスの帯では、赤い円が帯を2周しています。 それは、赤い円が内部に円板型射影平面[1]の中心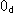を含んでいるからです。 その中心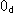を通る同心円の直径は、2点a,bで円板に移ります。
どの円も灰色のセンターラインを横切っていません。 すべての円が、円板型射影平面[1]の内部にとどまっているからです。 対応関係が
となっていることを忘れないでください。
それはよいとして、拡大図(*)とともにメビウスの帯を見ると、同心円の中心Oが、赤い円のループからまるごと離れているではありませんか。 どうしたことでしようか。
[5]: 真上から[1]を見ると、青い円の中にも同心円の中心Oがありません。
[6]: [3]を斜めにしたところです。 これで見ると、同心円の各円の立体的な配置がよくわかります。 円板型射影平面という平面上では、たしかに同心円状になっていました。 それが立体の面であるクロスキャップに移されると、3つの円とそれらの中心Oは同一の平面上にはありません。 ですから、[4]や[5]のようになるのです。
[7]: 円の内側とは中心のある側であるということに注意して、赤い円の内側を黄色くしたものです。 メビウスの帯と円板の両方が塗られています。 これで見ると、メビウスの帯ではセンターラインのある側が赤い円の外側になっています。
ここでまた気付きます。 このメビウスの帯のセンターラインは、クロスキャップの自己交差の交線に対応するものであり、それは無限遠直線からなるものですから、センターラインのある側は広大無辺なところだと考えることができます。 すると、赤い円の外側は、やはり「外側は内側より広い」という"常識"が通用するところではありませんか！
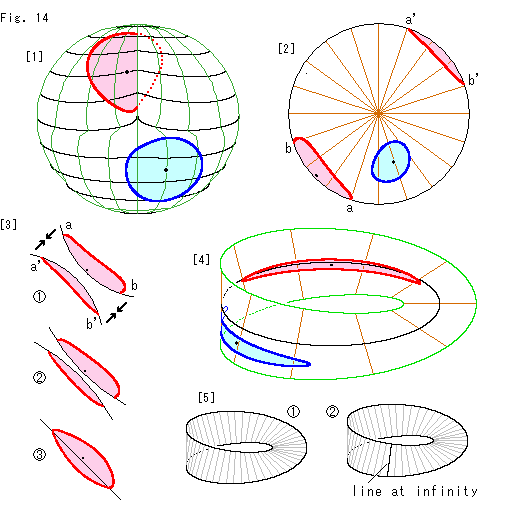Fig.14をご覧ください。
円板型射影平面上の射影平面における円をクロスキャップに移したものは、クロスキャップの自己交差の交線をけっして横切りません。 それでは、クロスキャップ上で円のように見える曲線を、自己交差の交線を横切らせて描くとどうなるでしようか。
[1]: 赤と青の曲線はクロスキャップで見た目に円らしくなるようにと描いたものですが、クロスキャップの面が球面のように単純ではので、適当にかたどっています。 その半径は、面の凹凸を無視して、中心からの直線距離で与えています。 点線のところは、自己交差の交線を横切った向こう側です。 (このクロスキャップの格子線は、窪みの様子がほぼ正面から見ても感じられるようにと描いただけのものです。)
[2]: 円板型射影平面上に移したものです。 クロスキャップの自己交差の交線を通っていた赤い閉曲線は、分断されて見えます。 円板型射影平面の対心点は同一視されているので、本当は切断されていません。
[3]: 円板型射影平面の円周に達している赤い閉曲線を見るときは、それを想わなければなりません。 たとえば、a,bで分断されてる方を裏返し、のようにa',b'で分断されてる方に対向させます。 そして黒い円弧と円弧を交わらせないで、矢印のように接近させていきます。 はその途中です。 両者が密着すると、のようになります。 ずいぶん扁平に見えますね。 円板型射影平面の円周に近づくと、半径方向の距離間隔が蜜になっているからです。
射影平面上の図としてこれを見るには、黒い線が無限遠直線であることを忘れてはなりません。 つまり、円板型射影平面の円周に達している図形は、その円周のところで無限に広がっているということです。 たんに対心点が同一視されている円板と、円板型射影平面であるものとは本質的に異なっているのです。 想って見るといっても、そこが違うのです。
[4]: 幸いなことに、メビウス型射影平面上に移してみると、円らしくは見えませんが、分断されずに、ちゃんと閉曲線になっています。 メビウス型射影平面のセンターラインが円板型射影平面の無限遠直線である円周だからです。 メビウス型射影平面のこのセンターラインのところは、実は無限に広がっているのです。
[5]: はふつうのメビウスの帯です。 そこにのように無限遠直線(line at infinity)を引くと、事態は一変します。 無限遠直線のところは、無限に広がったところですから。 しかし、そのメビウスの帯も単側であることに変わりはありません。
同様に、射影平面であるクロスキャップの自己交差の交線も無限遠直線であることを忘れてはなりません。 しかし、それは正しいのですが、私たちはクロスキャップをユークリッド的な形をしたものだとして、しばしば扱っています。 メビウスの帯では無限遠直線に近づくと図上のものが小さく見えるのを描きましたが、クロスキャップではそのような図は描いていません。 それは自己交差の交線の付近の様子をわかりやすく描けないからです。 それに、そうしなくても結果に違いのないことがほとんどだからです。
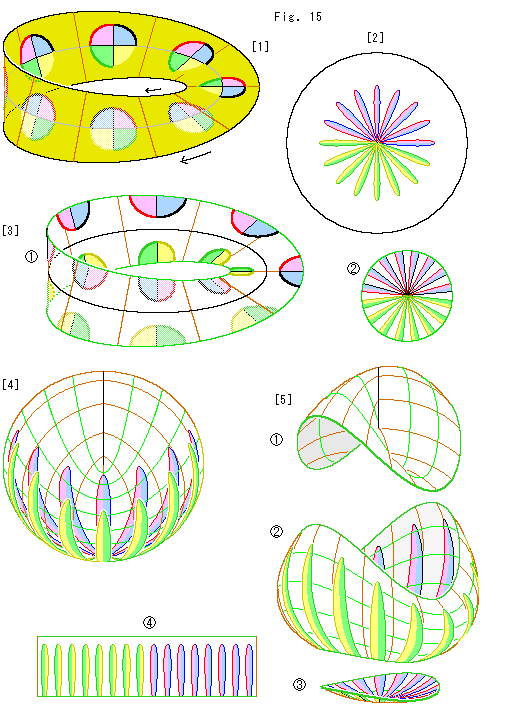
Fig.15をご覧ください。
MK型射影平面に視覚的な円を並べたものを他に移してみます。
[1]: 図のメビウスの帯はクラインの壷ですので、地色をつけて矢印を添えています。 円はふつうのコンパスで描いたもので、中心をセンターライン上にそろえています。 各円を四色に塗って、どの部分がどこだかを識別できるようにしています。 かすれた色のは、円自体には表裏があるので、それを表現したものです。
[2]: 円板型射影平面上に移すと、並んでいた円は菊花状になります。 各円は、MK型射影平面[1]から見て180捻じられると同時に、[1]のセンターライン上にあったすべての円の直径が円板型射影平面の中心である1点に絞られています。 [1]のセンターラインは、クロスキャップの底の点(射影平面円板型の中心)を線に引き伸ばしたものですから当然です。
[3]: 射影平面をメビウス型射影平面と円板に分解したものです。 この円板は円板型射影平面[2]の中心付近をくり抜いたものと同じです。 それ以外のところがメビウス型射影平面上で図のようになっています。 メビウス型射影平面上の円の部分が円板上の楔形と継ながらないように見えますが、との縁と縁を(抽象的に)貼り合わせれば、無論なめらかに継ながります。
[4]: 透かしたクロスキャップ上で見たものです。
[5]: そのクロスキャップを上下に3つに分離しました。 は自己交差の交線を含んでいます。 そこを除いた残りは、どう切ってもメビウスの帯にはなりません。 は円筒と同じですから、そのままで短冊に切り開くことができます。 そして底部は、押さえつければ、[3]の円板になります。
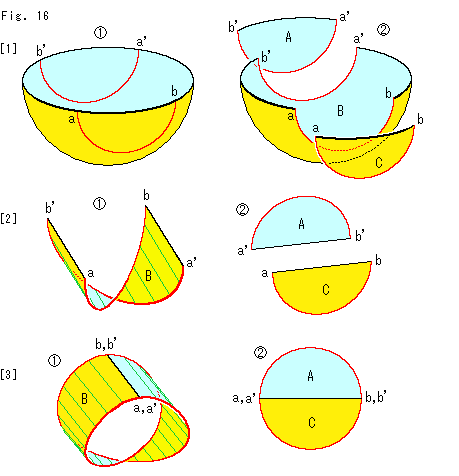
Fig.16をご覧ください。
上の方のFig.11の[3]でちょっとふれたことですが、メビウスの帯の作り方によって差異が生じることを見ておきます。 もちろん、その差異は本質的なものではありません。 しかし、ここでのようにすると、射影平面がメビウスの帯と円板からなってることが、見やすくなります。
[1]: 対心点の同一視を実行しようとする半球面です。 それをの赤い線に沿って切り、のようにA,B,Cに分離します。
[2]: 真中のBをのように、半球の黒い縁であったところを真直ぐにして、180捻じります。 右捻じりでも左捻じりでもかまいません。 AとCも縁であったところをのように真直ぐにします。 そして、Aを逆さまにします。 A,Cとも半円になっています。
[3]: 捻じたBの両端を継なぐと、メビウスの帯になります。 AとCの直径を継なぐと、円板になります。
メビウスの帯の色はもとのままですが、いまから色を塗れば、もちろん一色になります。 円板は表裏のあるふつうの円板です。 これも、上下で色分けする必要は、もうありません。
射影平面(半球面)をメビウスの帯と円板に分解するこの方法は、前に矢印付き四角形などでやったものの一つと同じです。 ここで注目したいのは、クロスキャップの自己交差の交線に対応する半球面の縁が、メビウスの帯上と円板上に分離しているということです。 そして、その自己交差の交線はメビウスの帯を横切っています。
自己交差の交線は、いうまでもなく無限遠直線です。 ですから、無限遠直線の全域をつかうことさえしなければ、このメビウスの帯も射影平面として用いることができます。 ただし、このメビウスの帯にはFig.7の対応づけが適用できません。
[前章] [次章] [目次]