第3部 射影幾何から双曲幾何へ
Ch.43 クラインの壷と射影平面 
クラインの壷と射影平面には似たところがありますね。 似て非なるものと見くらべていくことで、本当のものをよりよく知ろうとします。 見くらべるといっても、いろいろといじくってみるのです。
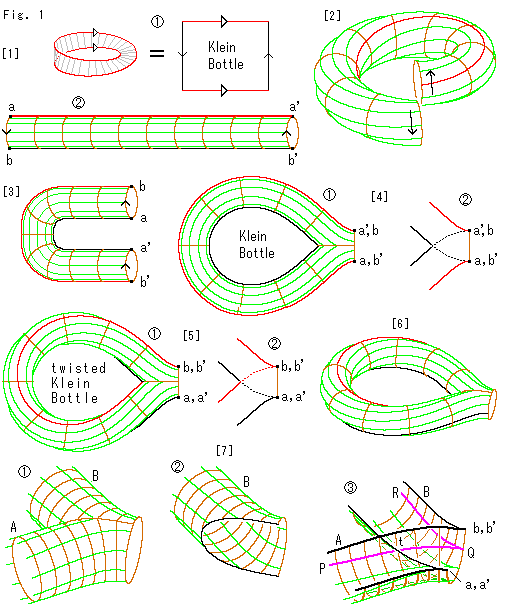 Fig.1をご覧ください。
Fig.1をご覧ください。
標準的なクラインの壷の絵はバランスのとれた格好をしていません。 対称な形をしたクラインの壷を工夫してみます。
[1]: クラインの壷である矢印付き四角形から出発します。 その四角形は、図のように向かい合った縁を同一視したメビウスの帯です。 まず、 の四角形の三角矢印の同一視を実行して、円筒
の四角形の三角矢印の同一視を実行して、円筒 にします。 メビウスの帯の縁や四角形の上下の辺を赤くしてあるのは図解のために染めたものです。
にします。 メビウスの帯の縁や四角形の上下の辺を赤くしてあるのは図解のために染めたものです。
[2]: 円筒をトーラスをつくるときのようにしてみると、よく知られているように、どのように捻じても矢印の向きがそろいません。
[3]: ところが、円筒をU字形にして眺めると、捻じらなくても矢印の向きがそろっています。
[4]: そこで、切口の向きを保ったままで、U字形のチューブの端を継なぎます。 チューブの面は貫通自在だとします。 そして、 のように切口と切口を重ね合わせます。
のように切口と切口を重ね合わせます。  は、その継がりぐわいを透かして見たものです。 まったく対称的な形です。
は、その継がりぐわいを透かして見たものです。 まったく対称的な形です。
[5]: 形としては、これでクラインの壷は出来上がっているのですが、クラインの壷であるメビウスの帯に対応させるためには、矢印の向きが一致していても、チューブを180 捻じらなければなりません。
捻じらなければなりません。  は、そうして捻じたものを真上から見たところです。 その切口の継がり具合は、
は、そうして捻じたものを真上から見たところです。 その切口の継がり具合は、 のようになっています。
のようになっています。
[6]: [5]を立体的に描いたものです。
[7]: チューブの継ぎ箇所をくわしく描いたものです。 図は[6]をもとに描いたものですが、面を捻じたものでなくても、様子は同じです。 捻じれがあってもなくても、形としては変わらないからです。 実際、ふつうにクラインの壷というときは、その面自体の捻じれは問題にしません。 ここで面自体の捻じれといっているのは、面の上の各点が捻じれの関係にあることを指しています。 つまり、クラインの壷であるメビウスの帯との関係を見るときに、捩れを含めた対応づけをすればよいのです。
外観は のように2つの脚A,Bからなる単純な二又です。
のように2つの脚A,Bからなる単純な二又です。  は一方の脚Aを切り離したもので、
は一方の脚Aを切り離したもので、 は上半分を取り除いたものです。
は上半分を取り除いたものです。  で見るように、面と面が貫通しあっています。 ピンク色の線は、脚の一方から他方へ移っていくときの一例です。 脚A,Bのどちらから来てもすぐに曲がらずに、切口に達してから他方へ進みます。 Aの点Pから来たピンクの曲線は、Bの面に点tで触れますが、そこでは曲がらずに、そのままAの面に沿って切り口の点Qまで行きます。 そして、そこでBの面に移り点Rへとすすみます。 この動き方は、クラインの壷の3次元モデルとしての約束です。
で見るように、面と面が貫通しあっています。 ピンク色の線は、脚の一方から他方へ移っていくときの一例です。 脚A,Bのどちらから来てもすぐに曲がらずに、切口に達してから他方へ進みます。 Aの点Pから来たピンクの曲線は、Bの面に点tで触れますが、そこでは曲がらずに、そのままAの面に沿って切り口の点Qまで行きます。 そして、そこでBの面に移り点Rへとすすみます。 この動き方は、クラインの壷の3次元モデルとしての約束です。
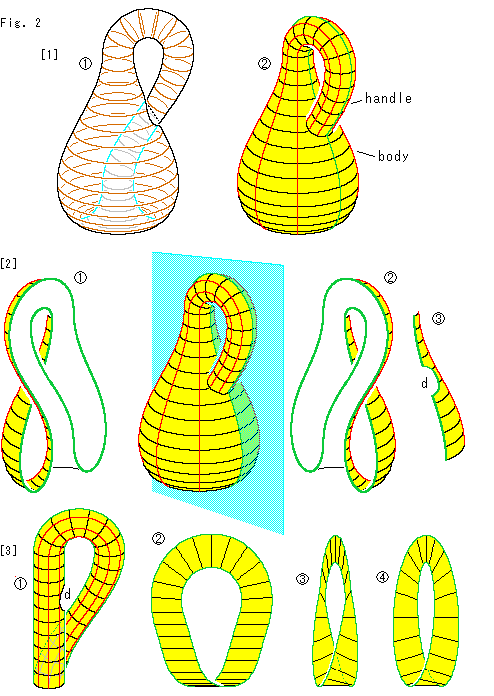
Fig.2をご覧ください。
クラインの壷はメビウスの帯からできていると聞いています。 標準的な形のもので、それを見てみます。
[1]: 透かして見ると のようになっていて、その外観は
のようになっていて、その外観は のようになっています。 便宜上、チューブ状のところをハンドル(handle)、とっくり状に膨らんだところをボディ(body)と名付けておきます。
のようになっています。 便宜上、チューブ状のところをハンドル(handle)、とっくり状に膨らんだところをボディ(body)と名付けておきます。
 [2]: クラインの壷を緑色の線に沿って左右に真っ二つに切ります。 左側は
[2]: クラインの壷を緑色の線に沿って左右に真っ二つに切ります。 左側は のようになっていて、右側は
のようになっていて、右側は のようになっています。
のようになっています。  は
は のハンドルで隠れていたところです。 ハンドルのための窪みdがあります。
のハンドルで隠れていたところです。 ハンドルのための窪みdがあります。  でも同様です。
でも同様です。
二分された と
と は、まったく対称な形で、右捻じり(right-handed)と左捻じり(left-handed)のメビウスの帯です。
は、まったく対称な形で、右捻じり(right-handed)と左捻じり(left-handed)のメビウスの帯です。
[3]: それを確かめるために、左半分のボディを細くして、 のようにします。 そして、窪みdをなくして押さえつけ、平たくして下部をU字形にします。 横から見ると、
のようにします。 そして、窪みdをなくして押さえつけ、平たくして下部をU字形にします。 横から見ると、 のようになっています。 この捩れをならすと、
のようになっています。 この捩れをならすと、 の見慣れたメビウスの帯になります。 右半分のも同様です。
の見慣れたメビウスの帯になります。 右半分のも同様です。
つまり、クラインの壷は、右捻じりと左捻じりの2つのメビウスの帯を貼り合わせたものだというわけです。 ただし、いうまでもなく貼り合わせの際には窪みdを作って、ハンドルをまたぐようにしなければなりません。
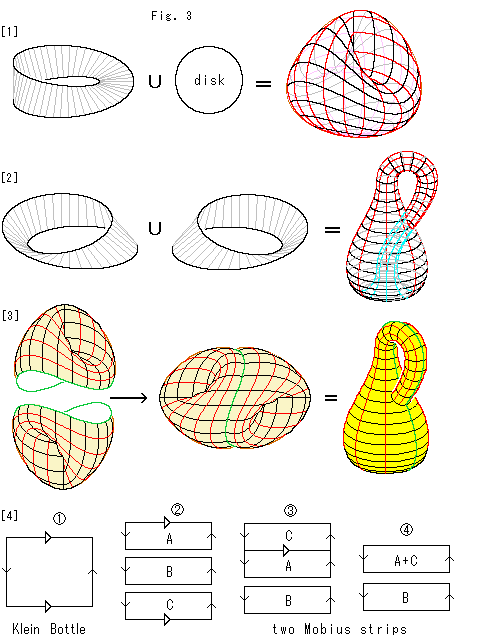
Fig.3をご覧ください。
1つのメビウスの帯に円板を貼れば、クロスキャップになります。 2つのメビウスの帯をくっつければ、クラインの壷になります。 また、底を抜いた2つのクロスキャップをドッキングさせれば、クラインの壷が得られます。
このような似かよった関連があるので、ならべて描いてみます。
[1]: クロスキャップができるときの模式図です。 記号Uは抽象的な貼り合わせです。
[2]: クラインの壷ができるときの模式図です。 右捻りと左捻りのメビウスの帯からクラインの壷が得られることを表現していますが、クラインの壷ができてしまえば、捻りの向きがどうであったには依存しません。
[3]: 真ん中の絵は、2つのクロスキャップのメビウスの帯に対応する部分を継なぎ合わせてできたクラインの壷です。 これも、まったく対称的な形です。 最右辺は、それを標準的なものに描きなおしたものです。 緑色の線が継ぎ目で、たがいに対応しています。
クラインの壷の対称ものと非対象なものを交換するには、2つのメビウスの帯に分解する過程を経なければなりません。
[4]: 矢印付き四角形でクラインの壷が2つのメビウスの帯に分解されるのを見たものです。 クラインの壷 を
を のようにA,B,Cの3つに水平に切ります。 左右の矢印
のようにA,B,Cの3つに水平に切ります。 左右の矢印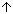 ,
,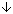 は、それぞれの四角形において同一視されるもので、A,B,Cの間での同一視を表すものではありません。 つぎに、AとCの三角矢印の辺を貼り合わせると、
は、それぞれの四角形において同一視されるもので、A,B,Cの間での同一視を表すものではありません。 つぎに、AとCの三角矢印の辺を貼り合わせると、 のようになります。 そして同一視を済ました三角矢印の辺を除くと、
のようになります。 そして同一視を済ました三角矢印の辺を除くと、 のように2つのメビウスの帯ができます。 ただし、矢印付き四角形のメビウスの帯では、右捻りと左捻りの区別がなされていません。
のように2つのメビウスの帯ができます。 ただし、矢印付き四角形のメビウスの帯では、右捻りと左捻りの区別がなされていません。
何度も似た図を描いていますが、2つのメビウスの帯がクラインの壷であることを示すものです。
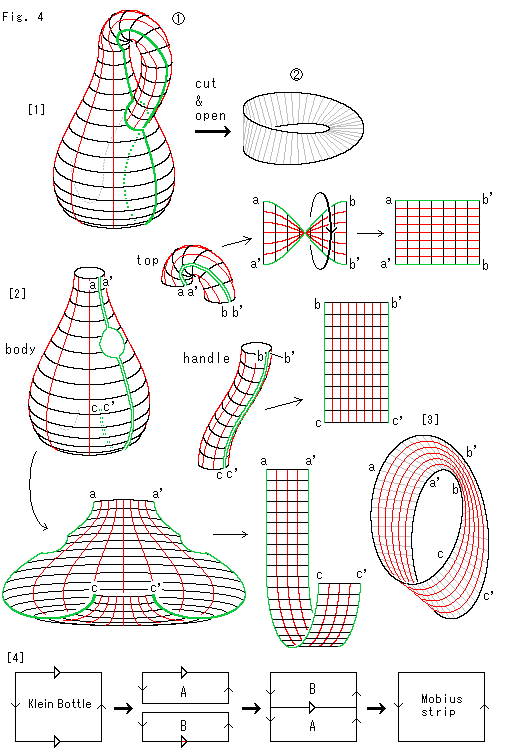
Fig.4をご覧ください。
上のFig.2ではクラインの壷を真っ二つに切って2つのメビウスの帯を得ましたが、切り方によっては、1つのメビウスの帯になります。
[1]: クラインの壷 を緑色の線のように切って開く(cut & open)と、メビウスの帯
を緑色の線のように切って開く(cut & open)と、メビウスの帯 ができます。
ができます。
[2]: どうしてそうなるのかを見るために、切り目をつけたクラインの壷を3つの部分、ボディ(body)とトップ(top)とハンドル(handle)に分けます。 それらを切り開いて、まず短冊に整形します。 トップのところでは180 捻じた切り方をしているのに注目してください。 そのため途中で矢印のように捩れを解いて整形します。
捻じた切り方をしているのに注目してください。 そのため途中で矢印のように捩れを解いて整形します。
[3]: 3つの短冊を継なぎもどしたものです。 メビウスの帯になっています。 トップの短冊の捩れは、短冊を継なぎもどしていくことで、自動的に復元されています。
[4]: ここでの切り方を矢印付き四角形で表現したものです。 これで見ると、クラインの壷からいくらでもメビウスの帯が取り出せますね。
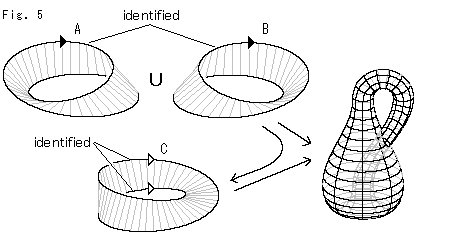 Fig.5をご覧ください。
Fig.5をご覧ください。
クラインの壷から得られるメビウスの帯は、切り方しだいで2つにもなり、1つにもなります。 それは逆に見て、メビウスの帯からクラインの壷を作る方法が異なっているからです。 2つのメビウスの帯A,Bでは、一方の縁を他方の縁と同一視(identify)すれば、クラインの壷になります。 1つのメビウスの帯Cでは、縁をそれと向かい合っている自分自身の縁と同一視することによって、クラインの壷になるのです。
それなら、(捩れがたがいに逆の)2つのメビウスの帯A,Bをクラインの壷にして、それから1つのメビウスの帯Cにすれば、2つのメビウスの帯から1つのメビウスの帯が得られることになりますね。 たしかにそうです。 けれども、2つのメビウスの帯A,Bから直接1つのメビウスの帯Cをつくることはできません。
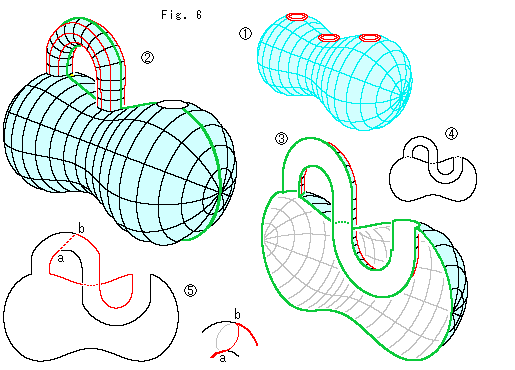
Fig.6をご覧ください。
 : 街で見かけた花瓶です。
: 街で見かけた花瓶です。
 : 面白い形なので、3つの穴にS字形のチューブを通して、クラインの壷にしてみました。 こんなのは、ご覧になったことがないでしよう。 均整のとれた格好になっています。
: 面白い形なので、3つの穴にS字形のチューブを通して、クラインの壷にしてみました。 こんなのは、ご覧になったことがないでしよう。 均整のとれた格好になっています。
 : こちら側を切り落として、内部を覗いたものです。 これがメビウスの帯になっているわけですね。
: こちら側を切り落として、内部を覗いたものです。 これがメビウスの帯になっているわけですね。
 : そのメビウスの帯に円板を張って射影平面を得ようとするのなら、円板の形は図のようになっていなければなりません。 内側も外側もない円を想ってください。
: そのメビウスの帯に円板を張って射影平面を得ようとするのなら、円板の形は図のようになっていなければなりません。 内側も外側もない円を想ってください。
 : このクラインの壷を赤い線のように8字形に切って開くと、1つのメビウスの帯になります。 赤いカットラインは黒い線に重なっているのですが、途中でabのように渡ります。 右下に描いてあるのは、そこを斜めから見たものです。 2点a,bは、このような8字形になるところなら、どこにとってもかまいません。
: このクラインの壷を赤い線のように8字形に切って開くと、1つのメビウスの帯になります。 赤いカットラインは黒い線に重なっているのですが、途中でabのように渡ります。 右下に描いてあるのは、そこを斜めから見たものです。 2点a,bは、このような8字形になるところなら、どこにとってもかまいません。
ところで、クラインの壷には内側も外側もないとよくいわれますが、あまり適切な表現とは思えません。 やはり、壷の面には表裏の区別がつけられないという方がよいでしよう。 実際、クラインの壷に水を注ぐことができるのですから。
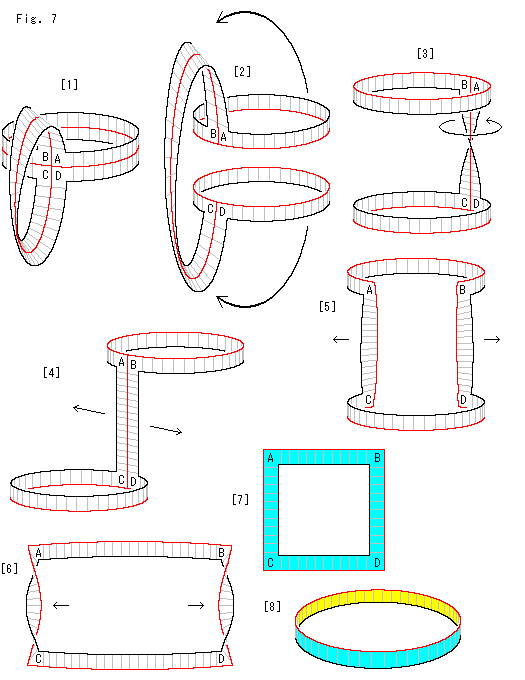
Fig.7をご覧ください。
捻じられていない円筒状の帯とメビウスの帯を十字にくっつけたものは、クラインの壷の一部です。 それをセンターラインで切ってみます。 ここでの図解は、あとの話の理解に役立つようにと、できるだけ細かにすすめます。
[1]: まず、円筒部を赤い線に沿って切ります。
[2]: 上下に分かれた円筒を矢印のように回転します。
[3]: すると、コの字形になり、メビウスの帯であったところが捻じれた垂直部分になります。 垂直部分は短く描いています。 そこを矢印のように回して、捻じれをときます。
[4]: こんどは縦の赤い線で切って、左右に引き離します。
[5]: 上部ABと下部CDの面を垂直に保って引き離していくと、垂直部AC,BDに新しい捻じれが生じます。 図では、いま右も左も90 くらい捻じれています。 捻じれの向きは左右で逆です。
くらい捻じれています。 捻じれの向きは左右で逆です。
[6]: さらに引き離していきます。
[7]: 左右の捩れは逆向きですので、キャンセルし合って、平坦な正方形の帯に描くことができます。こうなれば、バカでも表裏のあるものであることがわかります。 それで、こちら側の面を色づけしました。
捻じれが消えたのは、[2]でメビウスの帯のループを切断したのですから当然です。
[8]: この正方形を円筒に変形したものです。
十字形クラインの壷の正体は、切ってみれば、単純なループの帯だったわけですね。
つぎに十字形射影平面を切ってみようとするのですが、その前に捩れの基本的なことのいくつかを確かめておきます。
今後、捻じれを180 として、その左捻じりをL、右捻じりをRと表します。
として、その左捻じりをL、右捻じりをRと表します。
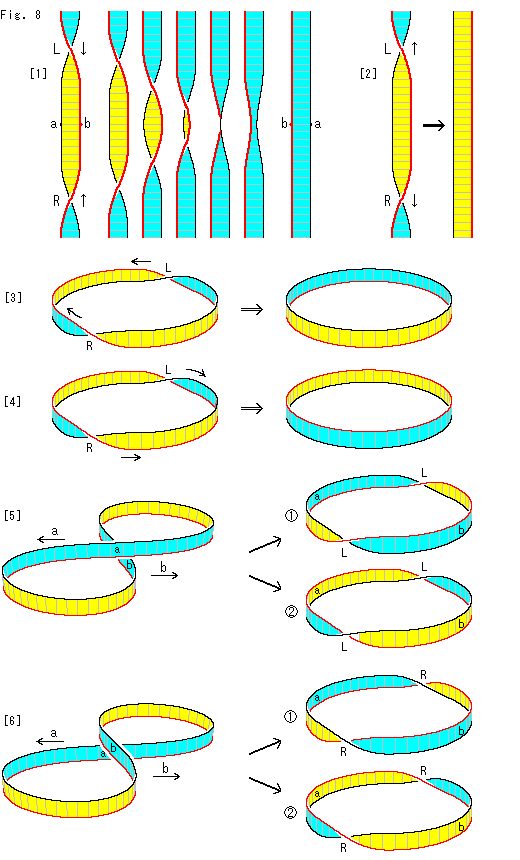
Fig.8をご覧ください。
[1]: 左の方の帯にはRとLの捻じりがあります。 上下端を固定しておいて、RとLを中央へ向けて滑らせていきます。 すると、当たり前のことですが、図の左から右へのように変化して、捻じれのないものになります。 RとLがキャンセルし合うからですね。 ここで注目しておきたいのは、見える表裏が一方だけになり、2つの捻じれRとLに挟まれていたところのabが逆にbaなるということです。
[2]: 同じ帯で、逆に中央を固定しておいて、Lを上へ、Rを下へ滑らせていくと、[1]とは逆の結果になります。
[3]: ループで同様なことをしてみます。 右の方を固定しておいて、RとLを左へ滑らせて捻じれをキャセルさせると、黒い縁が上になり、赤い縁が下になります。 そして、内側が水色、外側が黄色になります。
[4]: 同じループでも、逆に左の方を固定しておいて、RとLを右へ滑らせると、捻じれが解けることに変わりはありませんが、[2]とは逆の結果になります。
いずれも当然の話しですが、捻じれを見ていくときの混乱の原因になりがちです。
つぎは、捩れが発生する場合です。
[5]: 8字状のループは、蛇行しているだけで、捩れていないように見えます。 しかし、a,b付近を左右に引っぱってみると、Lが2つ現れます。 これは、左右に引っぱることによって捩れていないものから生じたのです。 つまり、8字状のループは図のように形を変えるだけで、わざと捻じらなくても、かってに捻じれるのです。 8字状のループは360 の潜在的な捩れをもっているわけです。(微分幾何などには、こんな用語はありません。)
の潜在的な捩れをもっているわけです。(微分幾何などには、こんな用語はありません。)
 はa付近を固定して引っぱったときで、
はa付近を固定して引っぱったときで、 はb付近を固定して引っぱったときです。
はb付近を固定して引っぱったときです。
[6]: この8字状のループは[5]のとは違って、aが下で、bが上になっています。 そして、a,b付近を左右に引っ張ると、こんどはRが2つできます。  はa付近を固定して引っぱったときで、
はa付近を固定して引っぱったときで、 はb付近を固定して引っぱったときです。
はb付近を固定して引っぱったときです。
2つの8字状のループ[5],[6]は、同じものを違う方向から見ているのではありません。 それは、捩れが生じているループを見比べれば明らかです。
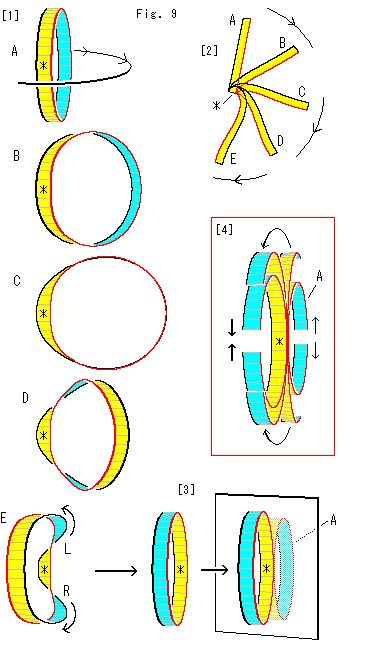
Fig.9をご覧ください。
もう一つ、捩れの基本的なことを見ておきます。
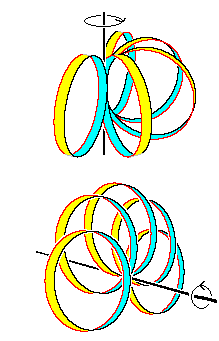 [1]: ループAを変形します。 *印のところを終始固定して、向こう側を矢印のようにこちら側へ回わします。 すると、A-B-C-D- と変化して、Eのようになります。
[1]: ループAを変形します。 *印のところを終始固定して、向こう側を矢印のようにこちら側へ回わします。 すると、A-B-C-D- と変化して、Eのようになります。
[2]: その様子を真上から見たものす。 右図のような回転ではありません。
[3]: Eでは、*印のところが向こう側になっていて、そこをLとRが挟んでいます。 *印のところはそのまま固定しておいて、LとRを矢印の方へ滑らせて、捩れをキャンセルさせると、このようにAと鏡映対照なものなります。
この過程では、*印のところをまったく動かしていないことに注目してください。
[4]: 同じ結果を得るには、この囲みのようにしてもよいのです。 ループAを一旦切って、その端を矢印のように回して、こちら側で継ぎなおします。 この手術は、[1]で見たことから問題はありません。 これは捩れの発生やキャンセルを考えなくてすすむので、好都合です。
それでは、十字形の射影平面を切っていくことにします。
Fig.10をご覧ください。
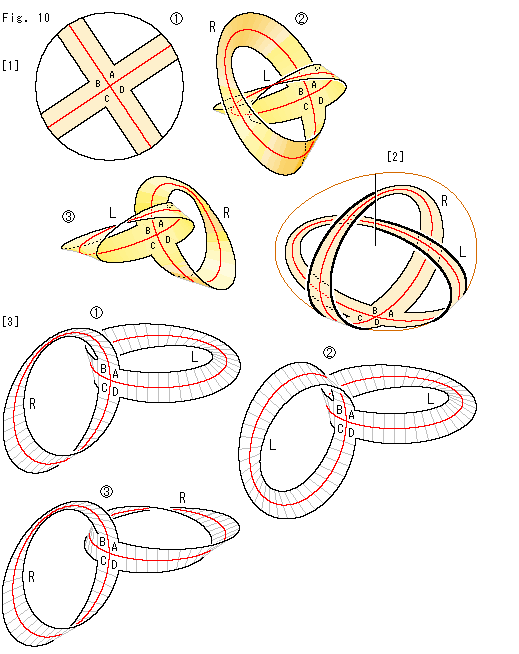
[1]: 円板型射影平面 から切り出した十字形の両端を同一視に合わせて継なぎます。
から切り出した十字形の両端を同一視に合わせて継なぎます。  は同じ側で継ないだもので、
は同じ側で継ないだもので、 は背中合わせに継ないだものです。 両者は、すぐ上のFig.9で見たように、交換可能です。 十字路ABCDのところを動かさないで、枝の1つを反対側へ移せばよいのです。 つまり、
は背中合わせに継ないだものです。 両者は、すぐ上のFig.9で見たように、交換可能です。 十字路ABCDのところを動かさないで、枝の1つを反対側へ移せばよいのです。 つまり、 と
と は同じものです。
は同じものです。
[2]: 透明なクロスキャップ上に這わせた十字形射影平面です。 背中合わせの十字形射影平面は、そのままではクロスキャップ上に這わせることができませんが、いつでも背中合わせでないものに変えることができるので、どんな十字形射影平面も図のようになります。
[3]: 見やすい背中合わせのものを見ていくことにします。 十字路の交差角(2本の赤いセンターラインのなす角)は、直角でなくてもかまわないのですが、見やすい直角にします。
十字形射影平面になっている2つのメビウスの帯の捩れには、LとRのとり方によって、 ,
, ,
, のように異なったものがあります。
のように異なったものがあります。  と
と は、向こう側の捩れとこちら側の捩れが同じ方向です。 それで、以下では
は、向こう側の捩れとこちら側の捩れが同じ方向です。 それで、以下では と
と をとりあげます。
をとりあげます。
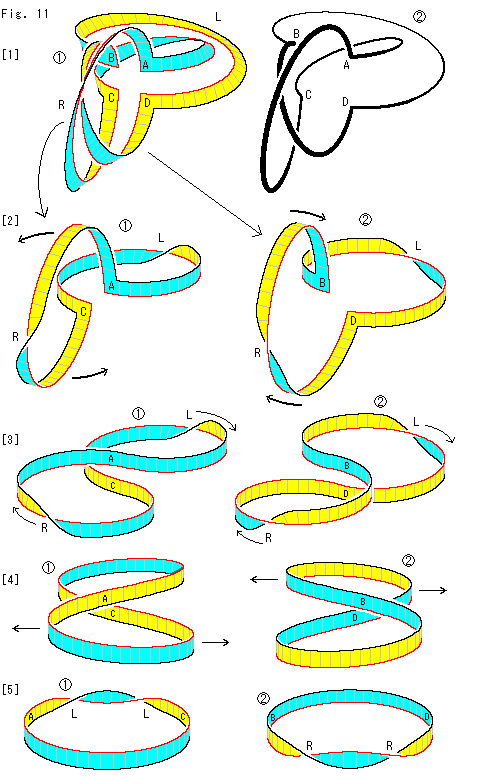
Fig.11をご覧ください。
RとLのメビウスの帯からなる十字形の射影平面を赤いセンターラインに沿って切ります。
[1]: すると、 のようになります。 2つのメビウスの帯の輪は切断されているので、表裏のあるものになっているはずです。 着色してみると図のように表裏を色分けできるので、間違いありません。
のようになります。 2つのメビウスの帯の輪は切断されているので、表裏のあるものになっているはずです。 着色してみると図のように表裏を色分けできるので、間違いありません。
できた2つのループが絡みあっているように見えます。 それを確かめるために、 の黒い縁だけをとって描いてみると、
の黒い縁だけをとって描いてみると、 のようになっています。 やはり、A,Cを通るループとB,Dを通るループは絡んでいます。
のようになっています。 やはり、A,Cを通るループとB,Dを通るループは絡んでいます。
以下、A,Cを通るループを左の列 に、B,Dを通るループを右の列
に、B,Dを通るループを右の列 に描いて、個別に見ていきます。 捻じれをシャープに描いて、RとLの捻じれ合がよくわかるようにしています。
に描いて、個別に見ていきます。 捻じれをシャープに描いて、RとLの捻じれ合がよくわかるようにしています。
[2]: こちら側を太い矢印のように90 ほど回転します。
ほど回転します。
[3]: すると、8字形になります。 RとLを、 ではAの方へ、
ではAの方へ、 ではDの方へ寄せてキャンセルさせます。
ではDの方へ寄せてキャンセルさせます。
[4]: RとLがキャンセルされて、AとDのところが裏返って上下が逆になっています。 表裏と上下は、面と縁の色で識別してください。 A,B,C,Dのラベルは、それと無関係に真直ぐに書いてあります。
矢印のように のこちら側を左右に引っ張ります。
のこちら側を左右に引っ張ります。  では、向こう側を引っ張ります。
では、向こう側を引っ張ります。
[5]: それぞれが、1つの輪になりました。 引っ張りによって新しい捻じれができています。  ではLが2つ、
ではLが2つ、 では、Rが2つです。
では、Rが2つです。
A,Cを通るループもB,Dを通るループも、その片側で360 捻じれた単純な輪だというわけです。
捻じれた単純な輪だというわけです。
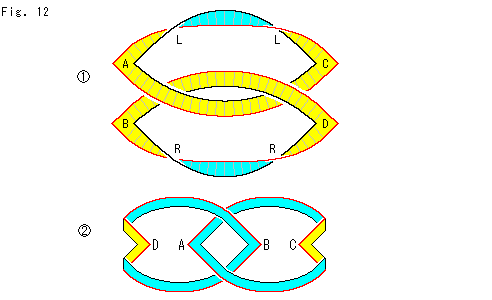
Fig.12をご覧ください。
上で得られた2つの輪をもとのように絡ませます。
 : 輪の赤い縁を外側へひねり、A,B,C,Dのところも元のように角張らせています。 上下のループは、まったく対照です。
: 輪の赤い縁を外側へひねり、A,B,C,Dのところも元のように角張らせています。 上下のループは、まったく対照です。
 : 変形の仕方を変えて、押さえつけてみたものです。 こうすると、A,B,C,Dの面の向きが初めと同じになります。
: 変形の仕方を変えて、押さえつけてみたものです。 こうすると、A,B,C,Dの面の向きが初めと同じになります。
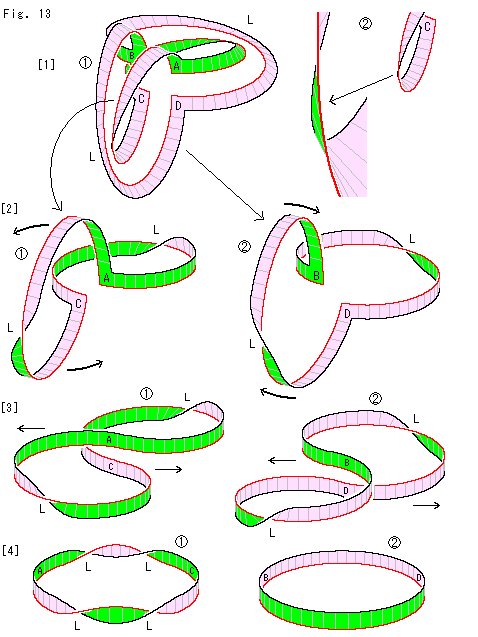 Fig.13をご覧ください。
Fig.13をご覧ください。
つぎに、LとLのメビウスの帯からなる十字形の射影平面を赤いセンターラインに沿って切ります。 図が上のと似ていて見誤りやすいので、面の色を変えて描きます。
[1]: 切ると、 のようになります。 こんどは、絡んでいません。
のようになります。 こんどは、絡んでいません。 は、A,Cを通るループのこちら側の見えにくいところを拡大したものです。 これで捩れの具合がよく見えます。
は、A,Cを通るループのこちら側の見えにくいところを拡大したものです。 これで捩れの具合がよく見えます。
[2]: 上のFIg.11と同様に行います。
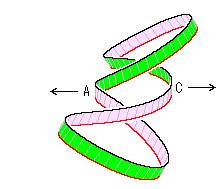
[3]: すると、8字形になります。 この は、捻じれをシャープにしなければ、右図のようになります。 そのA,Cの上下を保って、そのまま左右に引っぱっても、むろん同じ結果になります。
は、捻じれをシャープにしなければ、右図のようになります。 そのA,Cの上下を保って、そのまま左右に引っぱっても、むろん同じ結果になります。
[4]: それぞれが、1つの輪になりました。 もとの捻じれがLとLですので、そのキャンセルは起こっていません。 かわりに、 では、新しい2つの捻じれL,Lが加わって、360
では、新しい2つの捻じれL,Lが加わって、360 の捩れが2箇所でできています。
の捩れが2箇所でできています。  では、引っ張りによってできる新しい捻じれはR,Rですので、もとの捻じれL,Lとキャンセルし合って、捻じれのない輪になっています。
では、引っ張りによってできる新しい捻じれはR,Rですので、もとの捻じれL,Lとキャンセルし合って、捻じれのない輪になっています。
さて、このように十字形の射影平面を切ったものは、
(1) 360 捻じれた2つのループが絡んだもの(異なる向きの捻じりの2つのメビウスの帯からなる)
捻じれた2つのループが絡んだもの(異なる向きの捻じりの2つのメビウスの帯からなる)
か
(2) 2回360 捻じれたものと、まったく捻じれていないものの2つのループ(同じ向きの捻じりの2つのメビウスの帯からなる)
捻じれたものと、まったく捻じれていないものの2つのループ(同じ向きの捻じりの2つのメビウスの帯からなる)
になることがわかりました。
それでは、切られた射影平面の正体は(1),(2)のどちらでしようか? クロスキャップ上に移せるのは背中合わせでないものですが、そうであっても、(1),(2)のいずれかです。 十字になっている2つのメビウスの帯の捻じれRとLの組み合わせは、十字形の枝の方向と交差角によって定まります。 ですから、十字形の切り出し方によって(1)にも(2)にもなります。 つまり、(1),(2)のどちらか一方に限ってはいないのです。 それが、切って見た射影平面の正体です。
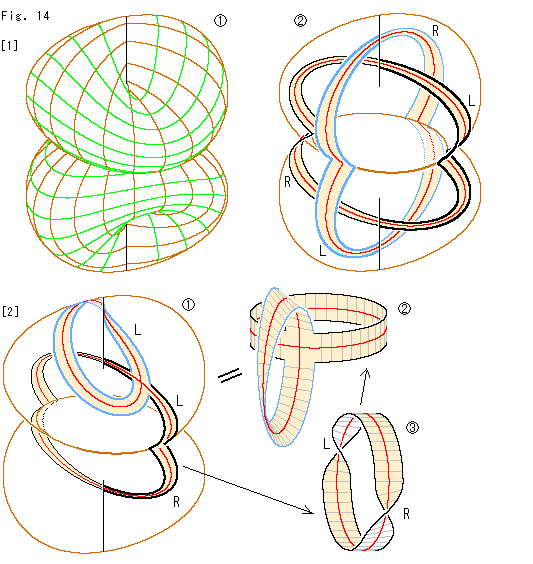
Fig.14をご覧ください。
[1]: 2つのクロスキャップの底を抜いてドッキングさせたもの を使ってみます。
を使ってみます。  は、
は、 を透明にして、上下の自己交差の交線を通る帯を2本這わせものです。 青い縁の帯も黒い縁の帯も捩れがRとLからなっていて、全体としてはねじれていません。
を透明にして、上下の自己交差の交線を通る帯を2本這わせものです。 青い縁の帯も黒い縁の帯も捩れがRとLからなっていて、全体としてはねじれていません。
[2]: このようになることを利用して、十字形のクラインの壷を得ます。  のように這わせた帯を取り出せば十字形のクラインの壷らしく見えるもの
のように這わせた帯を取り出せば十字形のクラインの壷らしく見えるもの になります。 それは、下側の自己交差の交線を通っているループが
になります。 それは、下側の自己交差の交線を通っているループが のようにLとRに捩れているのを寄せてキャンセルさせたからです。
のようにLとRに捩れているのを寄せてキャンセルさせたからです。
クロスキャップの底を抜いたものはメビウスの帯ですから、[1]の は2つのメビウスの帯をくっつけたものです。 底の切り口の縁がメビウスの帯の縁になっていることは、前に見ました。 そして、
クラインの壷は2つのメビウスの帯の縁と縁をくっつけたものですから、[2]のようにできるのは当然ですね。
は2つのメビウスの帯をくっつけたものです。 底の切り口の縁がメビウスの帯の縁になっていることは、前に見ました。 そして、
クラインの壷は2つのメビウスの帯の縁と縁をくっつけたものですから、[2]のようにできるのは当然ですね。
しかし、それなら、[1]の をそのままでクラインの壷だとしてもよいのでしようか。 クラインの壷をなすメビウスの帯は、右捻りRと左捻りLでなければなりませんが、ドッキングさせた2つのクロスキャップには何の区別もありません。 それは、完成してしまったクラインの壷から見れば、素材がどんなものであったかには依存しないのす。 現に、クラインの壷は1つのメビウスの帯としても切り開くことができるのですから。
をそのままでクラインの壷だとしてもよいのでしようか。 クラインの壷をなすメビウスの帯は、右捻りRと左捻りLでなければなりませんが、ドッキングさせた2つのクロスキャップには何の区別もありません。 それは、完成してしまったクラインの壷から見れば、素材がどんなものであったかには依存しないのす。 現に、クラインの壷は1つのメビウスの帯としても切り開くことができるのですから。
(捩れ方向が同じメビウスの帯については、次章で取り上げます。)
というわけで、[1]の はクラインの壷です。 それは標準的なクラインの壷のように内側も外側もない絵にはなっていませんが、同様な機能をもった自己交差の交線がついています。
はクラインの壷です。 それは標準的なクラインの壷のように内側も外側もない絵にはなっていませんが、同様な機能をもった自己交差の交線がついています。
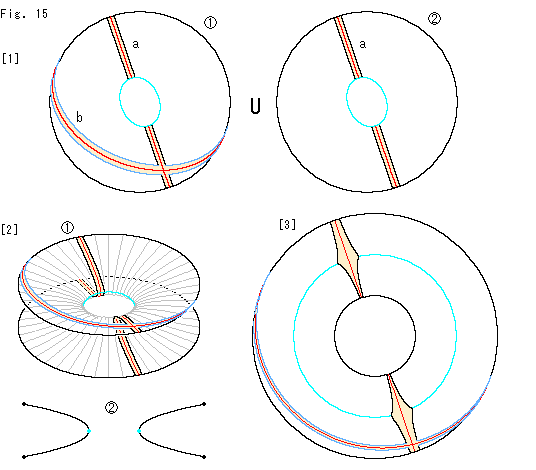 Fig.15をご覧ください。
Fig.15をご覧ください。
上の描画過程から気づいたことです。
[1]:  と
と は円板型射影平面で、ドッキングした上下のクロスキャップにそれぞれ対応しています。 水色の穴はドッキングの穴に当たります。
は円板型射影平面で、ドッキングした上下のクロスキャップにそれぞれ対応しています。 水色の穴はドッキングの穴に当たります。
帯aは十字形クラインの壷の円筒部分になるもので、帯bは、メビウスの帯部分になるものです。 帯aは穴のところへくると、もう一つの円板型射影平面の穴の縁へと継がっているものとします。 記号Uはそのことを表しています。 帯bは、円板型射影平面 上だけにあって、穴を避けています。
上だけにあって、穴を避けています。
[2]: 2つの円板型射影平面の穴と穴を密着させると、 のように1つの回転面にすることができます。
のように1つの回転面にすることができます。  は、その断面です。
は、その断面です。
[3]: 回転面はアニュラスと同じ(同相)です。 [2]の穴を大きくして、その穴の内側へ下の部分を押し込むと、図のようなアニュラスになります。 水色の円は、もとの2つの円板型射影平面[1]の穴の縁に対応しています。
これは、射影平面とクラインの壷とのつながりをこんなふうにも見れるというものです。
射影平面にもどります。 円板型射影平面から十字形射影平面を得たとき、四つの切り落としたところには注目しませんでした。 部分的な射影平面としては、メビウスの帯であってもよいので、十字形のものである必要はありません。 このメビウスの帯は、十字形射影平面と同様に、縁の同一視は考えていません。 ふつうのメビウスの帯です。
射影平面全体は、半球面や円板型射影平面やクロスキャップで表現されます。 それらからメビウスの帯を取り出す場合、切り落すのは1つの円板です。 円板の性質はよくわかっているので、たすかります。 そこで、メビウスの帯の切り出しをもう一度やってみます。
Fig.16をご覧ください。
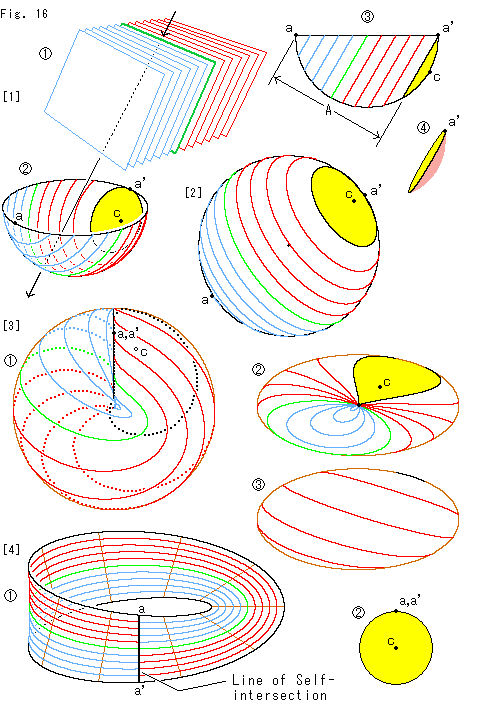
半球面を平行な平面で切ってメビウスの帯をつくります。
[1]: 等間隔の平行な平面 で斜めに半球面
で斜めに半球面 を切ります。
を切ります。  では、緑色のカットラインだけが大円です。
では、緑色のカットラインだけが大円です。  は、その切り口に平行な方向から見たものです。 平行な平面が赤道面の端a,a'と半球面上の点cをかすっています。 半球面を切って得られるメビウスの帯の最大巾がAになります。
は、その切り口に平行な方向から見たものです。 平行な平面が赤道面の端a,a'と半球面上の点cをかすっています。 半球面を切って得られるメビウスの帯の最大巾がAになります。  ,
, の黄色く塗った部分は、浅い椀状
の黄色く塗った部分は、浅い椀状 になっています。
になっています。
[2]: 半球を大きくして真上から見たところです。 これは、その縁の対心点が同一視されるものですから、円板型射影平面です。
[3]:  は、半球面を[2]の向きのままでクロスキャップにして真っ直ぐに立てたものです。 点線は曲線が向こう側を這っているところです。 それを真上から見ると
は、半球面を[2]の向きのままでクロスキャップにして真っ直ぐに立てたものです。 点線は曲線が向こう側を這っているところです。 それを真上から見ると のようになっており、真下から見ると
のようになっており、真下から見ると のようになっています。
のようになっています。
[4]: 黄色い領域([3]の では黒い点線の内側)を切り捨てます。 そして、メビウスの帯の巾を最大限Aにとって、点aと点a'を通るカットラインに沿って切り出します。 点aからはカットラインが伸びていませんが、2点a,a'は同一視されているので、問題ありません。 つまり、そのカットラインは、点cを囲んでいる黒い曲線です。 そうしてできたメビウスの帯が
では黒い点線の内側)を切り捨てます。 そして、メビウスの帯の巾を最大限Aにとって、点aと点a'を通るカットラインに沿って切り出します。 点aからはカットラインが伸びていませんが、2点a,a'は同一視されているので、問題ありません。 つまり、そのカットラインは、点cを囲んでいる黒い曲線です。 そうしてできたメビウスの帯が で、切り落とした椀状のところが円板
で、切り落とした椀状のところが円板 になっています。 メビウスの帯を横切っている黒い線aa'はクロスキャップの自己交差の交線(Self-intersection pivot)に対応したところです。
になっています。 メビウスの帯を横切っている黒い線aa'はクロスキャップの自己交差の交線(Self-intersection pivot)に対応したところです。
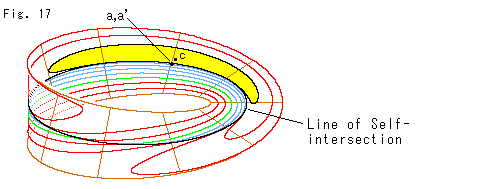
Fig.17をご覧ください。
こころみに、上のクロスキャップからメビウス型射影平面をつくるときの要領でメビウスの帯を取り出してみます。 カットラインをたんなる曲線と見立てます。 できたものを見ると、黄色い領域が含まれています。 自己交差の交線がセンターラインになっています。 上と比べると、当然ですが、曲線のパターンがずいぶん違っていますね。
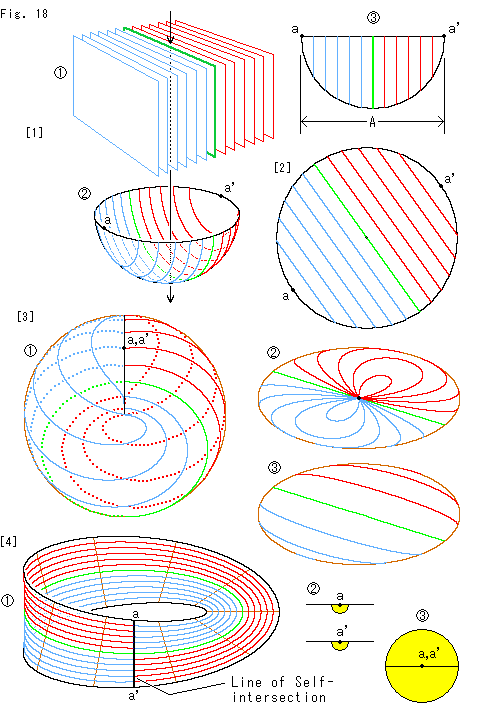
Fig.18をご覧ください。
こんどはカット平面を垂直にしてみます。
[1]: カット平面 を真っ直ぐに降ろして、半球面
を真っ直ぐに降ろして、半球面 を切ります。
を切ります。  では、切り出すメビウスの帯の最大巾をAにとります。
では、切り出すメビウスの帯の最大巾をAにとります。
[2]: 半球面を上から見たもので、円板型射影平面と同じものです。
[3]: クロスキャップ 上に点a,a'も移されていますが、そこから伸びるカットラインはありません。
上に点a,a'も移されていますが、そこから伸びるカットラインはありません。  を真上から見ると
を真上から見ると のようになっており、真下から見ると
のようになっており、真下から見ると のようになっています。
のようになっています。
[4]: 2点a,a'を微小な大きさをもったものだとして、最大巾Aのメビウスの帯にしたのが です。 これは、Fig.16の[4]とまったく同じですが、点a,a'には身勝手な考えを採り入れています。
です。 これは、Fig.16の[4]とまったく同じですが、点a,a'には身勝手な考えを採り入れています。  のように点aの極く近いところにカットラインが通っているとしたのです。 このようにすると、クロスキャップのほぼ全体をメビウスの帯として覆い尽くすことができます。
のように点aの極く近いところにカットラインが通っているとしたのです。 このようにすると、クロスキャップのほぼ全体をメビウスの帯として覆い尽くすことができます。  は、そうしたときの円板です。
は、そうしたときの円板です。
この点a,a'のところの考え方には異論も議論もあるので、後でもう一度考えます。
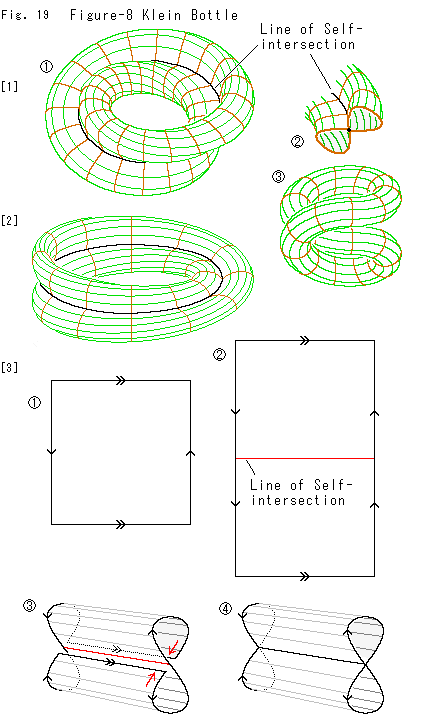
Fig.19をご覧ください。
この章のはじめにバランスのよいクラインの壷をつくりました。 バランスのよい格好のものに、8字形クラインの壷(Figure-8 Klein Bottle)とよばれているモデルもあります。 それを見ておきます。
[1]: それはメビウスの帯の断面を8字形に膨らませたもの です。 断面は
です。 断面は のようになっています。 そのセンターラインが自己交差の交線になっています。
のようになっています。 そのセンターラインが自己交差の交線になっています。
この形は、輪になったチューブを のように二重巻きにして、上を下の内側へ押し込んで線接触で密着させたものと同じです。 そして、線接触のところを自己交差の交線だとすれば、8字形クラインの壷になります。 ただし、その工作過程で生じる面自体の余分な捩れはないものとしてのことです。
のように二重巻きにして、上を下の内側へ押し込んで線接触で密着させたものと同じです。 そして、線接触のところを自己交差の交線だとすれば、8字形クラインの壷になります。 ただし、その工作過程で生じる面自体の余分な捩れはないものとしてのことです。
[2]: 上のようなダイナミックに描かれた8字形クラインの壷をよく見かけます。 しかし、そんなのは、きっちり観察するには不向きですね。 私たちになじみやすい形に変えました。 これは遠くから見ると、メビウスの帯に見えます。
[3]: 8字形クラインの壷がふつうのクラインの壷と同じものであることを確かめます。 そのために、クラインの壷の矢印つき四角形から8字形クラインの壷が得られる工夫をしてみます。
 : ふつうのクラインの壷の矢印つき四角形です。
: ふつうのクラインの壷の矢印つき四角形です。
 : その中ほどに自己交差の交線を設けます。 上下に引き伸ばして感じとりやすく描いています。
: その中ほどに自己交差の交線を設けます。 上下に引き伸ばして感じとりやすく描いています。
 : 上下を赤い矢印の向きに曲げて自己交差の交線上で突き合わせます。
: 上下を赤い矢印の向きに曲げて自己交差の交線上で突き合わせます。
 : 突き合わせて上下の辺の同一視が完了したところです。 上下の辺は、いま自己交差の交線に同化されています。 矢印
: 突き合わせて上下の辺の同一視が完了したところです。 上下の辺は、いま自己交差の交線に同化されています。 矢印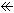 を消しています。
を消しています。
自己交差の交線上で交わっている2つの面は、そこではたがいに無関係ですから、このように変形したものの機能は、矢印つき四角形のと変わりありません。
左右の辺の同一視は、その両端をメビウスの帯と同様に捻じて継なげば、完了します。 そして、8字形クラインの壷が出来上がります。 これで確かめられました。
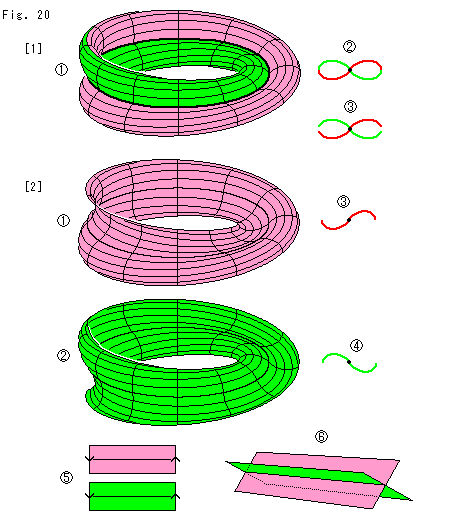
Fig.20をご覧ください。
8字形クラインの壷を分割をしてみます。
[1]: 8字形クラインの壷 も、もちろん単側ですので、本来色分けできないのですが、意図的に塗り分けしています。 その断面は
も、もちろん単側ですので、本来色分けできないのですが、意図的に塗り分けしています。 その断面は のようになっています。 全周にわたって断面を
のようになっています。 全周にわたって断面を のように切ります。
のように切ります。
[2]: すると、自己交差で続いている2つの曲面 と
と に分離できます。
に分離できます。  ,
, は右端で見た断面です。 断面はまがっていますが、どちらも、捻りが同じ向きのメビウスの帯です。
は右端で見た断面です。 断面はまがっていますが、どちらも、捻りが同じ向きのメビウスの帯です。
短冊に切り開くと、 のように描くことができます。 センターラインは自己交差の交線です。そして、もとの8字形クラインの壷にするには、
のように描くことができます。 センターラインは自己交差の交線です。そして、もとの8字形クラインの壷にするには、 のように自己交差の交線を通して挟み合わせて、後戻りしていけばよいのです。
のように自己交差の交線を通して挟み合わせて、後戻りしていけばよいのです。
2つのメビウスの帯を貼り合せることが、このようにしてみると、物理的に可能だとすら思ってしまいますね。 本当は不可能であることを見出すのに、逆にまごつくではありませんか。
これまでに見てきたことから、クラインの壷は
1つのメビウスの帯
2つの同じ向きに捻じたメビウスの帯
2つの反対向きに捻じたメビウスの帯
のいずれからでも得られることがわかりました。
自己交差とは、なんと都合のよいものではありませんか。 自己交差は、4次元の世界のことを3次元の世界で実現してくれる手段です。
なぜ、自己交差を採り入れなければならないのかを振り返ってみると、
無限の彼方を含めて考えるには、半球面の対心点の同一視が必要である。
平面での話だが、2次元である平面上には描けないので、曲面を平面とみなして3次元化した。
そうしても、ふつうに描くことは不可能である。
そこで、
4次元の世界でなら可能というものを「自己交差」をつかって3次元の世界で描いた。
というわけです。
標準形のクラインの壷をつくるときにボディに穴を開けてハンドルを通しました。 しかし、自己交差の考えでいけば、穴を開ける必要はありません。
[1]: 従来の方法でクラインの壷をつくる場合です。 ボディに穴(hole)が開けられています。
[2]: 自己交差の考えによって、ボディに穴を開けていません。 このままで、スッとハンドルをボディの中へ挿入することができます。 ボディには何の傷もつきません。
 Fig.22をご覧ください。
Fig.22をご覧ください。
一番左が標準形のクラインの壷の断面です。 面と面が 印のところで自己交差しています。 図の矢印のように変形していくと、Fig.1で見たチューブのクラインの壷になります。 左の方で2つあった
印のところで自己交差しています。 図の矢印のように変形していくと、Fig.1で見たチューブのクラインの壷になります。 左の方で2つあった 印が途中で1つになっています。 もちろん、逆に変形していくこともできます。 つまり、チューブのクラインの壷は標準形のクラインの壷と同じであることが、連続的な変形によって確かめられたというわけです。
印が途中で1つになっています。 もちろん、逆に変形していくこともできます。 つまり、チューブのクラインの壷は標準形のクラインの壷と同じであることが、連続的な変形によって確かめられたというわけです。
ところで、射影平面のモデルとしても、ローマン曲面とかボーイ曲面とかいった均整のとれたものがあるそうですが、いまの私たちには無用に思えるので、触れずにおきます。
ある数学者から「双曲幾何をするのに、なぜトポロジーをやるのか」と問われたことがあります。
平行線は無限の彼方で交わると仮定することで双曲幾何が生まれました。 ところが、その円板モデルはいわゆる開円板であって、無限遠を含んでいないのです。 上半平面のモデルでも同様です。 しかし円板モデルは、無限遠を直接あつかう射影幾何から作られます。 そのため、射影幾何へ進もうとメビウスの帯やクロスキャップをいじくってきたわけです。
円板モデルに無限遠が含まれていないのは、モデルの欠陥だと感じられるではありませんか。 しかし、円板モデルの円周が無限遠直線だとすると、その円周の対心点を同一視しなければならないことになります。 そして、円板モデル上のこれまでの話が総崩れしてしまいます。 これまでの話を維持しながら、無限遠を含むモデルは考えられないものでしょうか?
それには、測度とか無限遠の近傍といったものを取り入れるべきだそうです。 これも後で考えてみることにします。
ともかく、半球面の対心点の同一視にともなうことに一通りふれました。
[前章] [次章] [目次]
 Fig.1をご覧ください。
Fig.1をご覧ください。
 [2]: クラインの壷を緑色の線に沿って左右に真っ二つに切ります。 左側は
[2]: クラインの壷を緑色の線に沿って左右に真っ二つに切ります。 左側は

 Fig.5をご覧ください。
Fig.5をご覧ください。



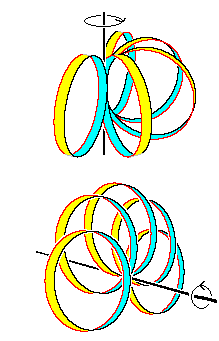 [1]: ループAを変形します。 *印のところを終始固定して、向こう側を矢印のようにこちら側へ回わします。 すると、A-B-C-D- と変化して、Eのようになります。
[1]: ループAを変形します。 *印のところを終始固定して、向こう側を矢印のようにこちら側へ回わします。 すると、A-B-C-D- と変化して、Eのようになります。

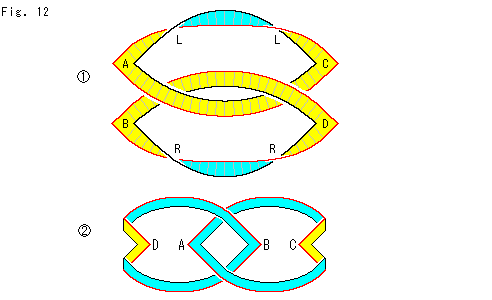
 Fig.13をご覧ください。
Fig.13をご覧ください。

 Fig.15をご覧ください。
Fig.15をご覧ください。





