第3部 射影幾何から双曲幾何へ
Ch.44 紙細工 (3) 
いろいろと紙細工をして考えます。 ここでも180 の右捻りをR、左捻りをLと表すことにします。
の右捻りをR、左捻りをLと表すことにします。
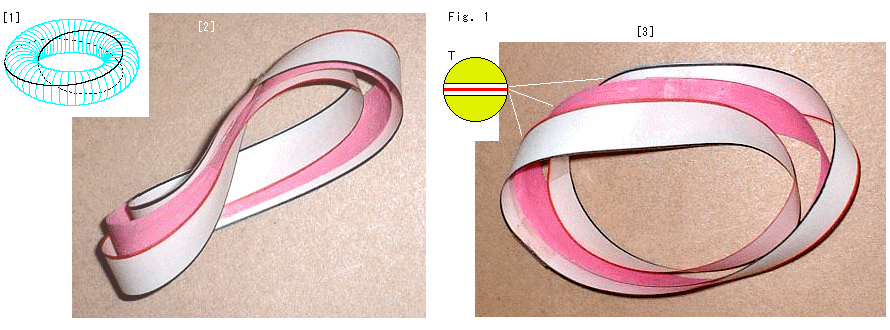 Fig.1をご覧ください。
Fig.1をご覧ください。
[1]: 以前に、変形しやすいトーラスにナイフを入れて、トーラス自体を削ることなくメビウスの帯を切り出しました。 黒い曲線が切った跡です。
[2]: 写真は、そのときのメビウスの帯とそれに接していたトーラスの面を紙細工にしたものです。 赤い帯がメビウスの帯で、白い帯がそれに密着していたトーラス側の面です。 面と面の間をすこしほぐして、分かりやすいようにしています。 白い帯には表裏があるので、縁を茶色と黒色で色分けしています。
[3]: 向きを変えて撮ったものです。 Tはトーラスの断面です。
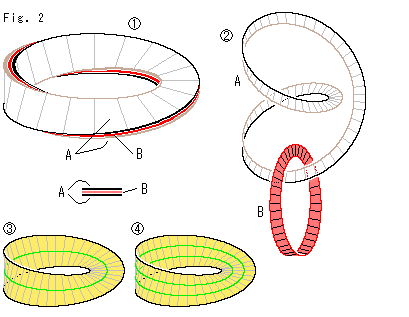
Fig.2をご覧ください。
写真ではきっちりしたところが巧く撮れないので、実際の紙細工を観察して作図しました。
ほぐさないで見ると、 のように3層になっているメビウスの帯です。 帯にちょっと厚みをつけてわかりよいように描いています。 ほぐしていくと、
のように3層になっているメビウスの帯です。 帯にちょっと厚みをつけてわかりよいように描いています。 ほぐしていくと、 のようになります。
のようになります。
この のAは前にも描いたものですが、それはクロスキャップの上部を細工して得られたものでした。 これはまた、メビウスの帯を
のAは前にも描いたものですが、それはクロスキャップの上部を細工して得られたものでした。 これはまた、メビウスの帯を のようにセンターラインで切っても得られます。
のようにセンターラインで切っても得られます。  のようにメビウスの帯を2周して切れば、AとともにBもこの図と同じものになります。
のようにメビウスの帯を2周して切れば、AとともにBもこの図と同じものになります。
メビウスの帯は、反対側の面も舐めて2周しても360 までしか捻じれません。 それなのに、メビウスの帯に密着していた帯Aが、360
までしか捻じれません。 それなのに、メビウスの帯に密着していた帯Aが、360 の2倍も捻じられているって、本当でしようか。
の2倍も捻じられているって、本当でしようか。
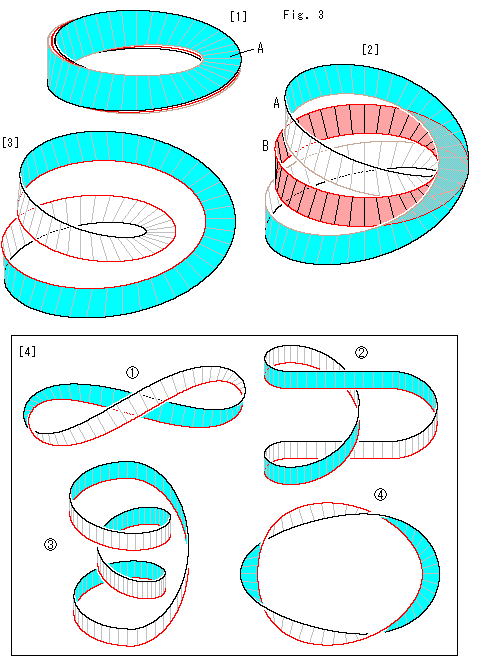 Fig.3をご覧ください。
Fig.3をご覧ください。
[1]: 水色のところは、Fig.2のループAです。 ループAには表裏があるので、色分けできます。
[2]: ループAの左の方をメビウスの帯Bから少し上下に引き離したところです。 白い裏面が現れています。
[3]: メビウスの帯Bを省いて、右の方を左右にずらせたところです。 縁の茶色を目立つ赤色にしています。 これを見るかぎり、捻れは360 だと思えますね。
だと思えますね。
[4]: さらにほぐしてみると、 ,
, ,
, ,
, のような色々な姿態を現します。 そのうちの
のような色々な姿態を現します。 そのうちの を見ると、たしかに360
を見ると、たしかに360 の2倍も捻れています。 ほぐす過程で、切って捻じて継なぐようなことは一切していません。 それなのに、どうしてこうなったのでしようか?
の2倍も捻れています。 ほぐす過程で、切って捻じて継なぐようなことは一切していません。 それなのに、どうしてこうなったのでしようか?
おおまかに見ると、[3]は輪が2つのコイルです。 この は1つの輪です。 360
は1つの輪です。 360 の捻れが輪に潜在していたように思えます。
の捻れが輪に潜在していたように思えます。
それを確かめましょう。 まずは、簡単なものからあたってみます。
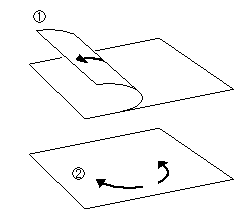
紙は、右図の のようには曲げやすいものですが、面自体を
のようには曲げやすいものですが、面自体を のように歪めようとしてもほとんどできません。 けれども、極端なことさえしなければ、なめらかに捻ることができます。 それは顕微鏡的な僅かな歪みや伸縮が積み重ねられるからです。 でも、あまり引っ張ると形が崩れてしまいます。
のように歪めようとしてもほとんどできません。 けれども、極端なことさえしなければ、なめらかに捻ることができます。 それは顕微鏡的な僅かな歪みや伸縮が積み重ねられるからです。 でも、あまり引っ張ると形が崩れてしまいます。
ゴムのシートなら、 の歪めもかなりできます。 いまからする実験の図は、それを使用したものですが、紙でやっても十分見て取ることができます。
の歪めもかなりできます。 いまからする実験の図は、それを使用したものですが、紙でやっても十分見て取ることができます。
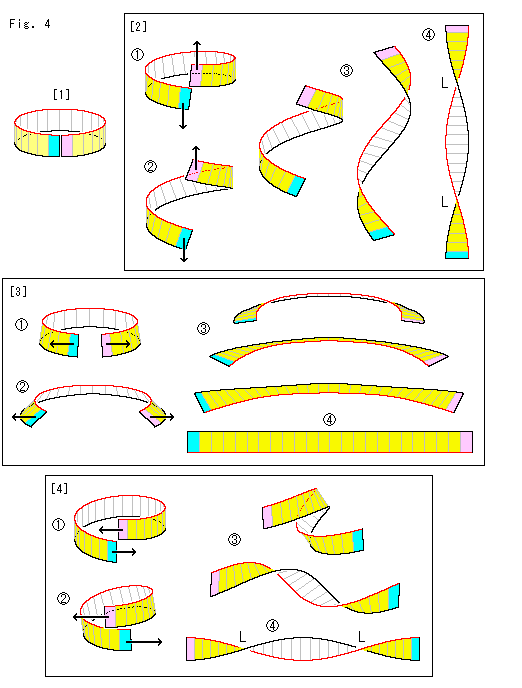
Fig.4をご覧ください。
[1]: 紙を円筒にして、一箇所を切ったものです。 外側を黄色く塗り、切った両端を見分けやすくするために水色とピンクで色づけしています。
[2]:  のように、ピンクの端を上へ水色の端を下へ引っ張ります。 両端をこちら側へ向けたままで、かるく持って引っ張ると、それにつれて両端が時計回りに回転しながら
のように、ピンクの端を上へ水色の端を下へ引っ張ります。 両端をこちら側へ向けたままで、かるく持って引っ張ると、それにつれて両端が時計回りに回転しながら ,
, ,
, となり、最後に
となり、最後に のようになります。 [1]とくらべると、両端が時計回りに90
のようになります。 [1]とくらべると、両端が時計回りに90 ずつ回転しています。 そして、180
ずつ回転しています。 そして、180 の左捻れLが2つで360
の左捻れLが2つで360 捻じれた短冊になっています。 水平な回転は一切与えなかったのに、どうしてでいようか?
捻じれた短冊になっています。 水平な回転は一切与えなかったのに、どうしてでいようか?
[3]: こんどは切った円筒を のように、左右に引き離してみます。 すると、
のように、左右に引き離してみます。 すると、 ,
, のようになり、最後は
のようになり、最後は になります。 まったく捻じれていません。
になります。 まったく捻じれていません。  とくらべると、縁の上下が逆になっているだけです。
とくらべると、縁の上下が逆になっているだけです。
[4]: ピンクの端を上に水色の端を下にずらします。 そして、ピンクの端を左へ、水色の端を右へ引っ張ります。 すると、 ,
, を経て、
を経て、 の360
の360 捻じれた短冊になります。 結果は[1]と同じですが、両端はまったく回転していません。
捻じれた短冊になります。 結果は[1]と同じですが、両端はまったく回転していません。
これらの実験で、
360 の捻じれは、たてよこを問わずリングがしぼむように引っ張れば、生じる
の捻じれは、たてよこを問わずリングがしぼむように引っ張れば、生じる
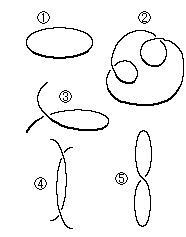 ということがわかりました。
ということがわかりました。
ここでリングとよんでいるのは、右図のようなものを指しています。  はふつうにリングといわれているものですが、他はそれに類して見えるものです。
はふつうにリングといわれているものですが、他はそれに類して見えるものです。  は3つのリングからなるもので、
は3つのリングからなるもので、 ,
, は1つのリング、
は1つのリング、 は2つのリングです。 もちろん、これらの数は見る方向によって変わりますが、見えているままで数えます。
は2つのリングです。 もちろん、これらの数は見る方向によって変わりますが、見えているままで数えます。
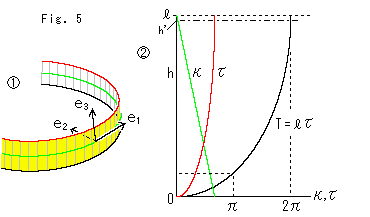 Fig.5をご覧ください。
Fig.5をご覧ください。
計算式でどうなるか見てみます。 上のFig.4の[2]では、円筒のセンターラインが円から螺旋になり、直線へと変化しています。 微分幾何では、点が空間曲線上を走るとして、 の直交する矢線のよに速度(接線)ベクトル
の直交する矢線のよに速度(接線)ベクトル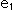 、加速度(主法線)ベクトル、従法線ベクトル
、加速度(主法線)ベクトル、従法線ベクトル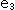 をとって、曲率
をとって、曲率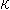 (カッパー)とか捻(れい)率
(カッパー)とか捻(れい)率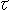 (タウ)といったものを用います。 さいわいにも、この螺旋はいわゆる常螺旋ですから、簡単に計算できます。 捩れは、
(タウ)といったものを用います。 さいわいにも、この螺旋はいわゆる常螺旋ですから、簡単に計算できます。 捩れは、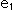 を軸として回転する
を軸として回転する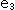 の回転角の合計です。
の回転角の合計です。
縦軸を螺旋の高さhにとり、横軸を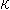 ,
,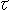 ,Tとしてグラフにしてみると、
,Tとしてグラフにしてみると、 のようになっています。 Tは、捩率
のようになっています。 Tは、捩率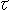 にセンターラインの長さ
にセンターラインの長さ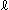 を掛けたもので、高さhにおける全体としての捩れです。 螺旋が伸びきって h =
を掛けたもので、高さhにおける全体としての捩れです。 螺旋が伸びきって h = 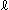 になると、捩れTが360
になると、捩れTが360 になるのがわかります。 この捩れTはセンターラインの捩れですが、帯の捩れと一致しています。 直線の捩率
になるのがわかります。 この捩れTはセンターラインの捩れですが、帯の捩れと一致しています。 直線の捩率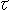 は0ですが、センターラインが真っ直ぐになったときのそれは、螺旋の極限として計算しています。
は0ですが、センターラインが真っ直ぐになったときのそれは、螺旋の極限として計算しています。
はじめの円筒のときは、帯の縁とセンターラインの長さは同じです。 ところが螺旋になって帯に捩れが生じてくると、その分だけ帯の縁の長さを伸ばして両端をセンターラインとそろえなければなりません。 それを帯がゴムでできているものだとしてカバーしています。 h'は、そのような伸縮がなされない場合の螺旋の伸ばし得る高さです。 h'と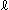 との差は、帯の巾をあまり大きくとらなければ、さほどのことはありません。
との差は、帯の巾をあまり大きくとらなければ、さほどのことはありません。
上のFig.4でいったリングのことは、円筒の場合だけでなく、アニュラスやメビウスの帯にも当てはまるはずです。 ねんのために、メビウスの帯でどうか確かめておきます。
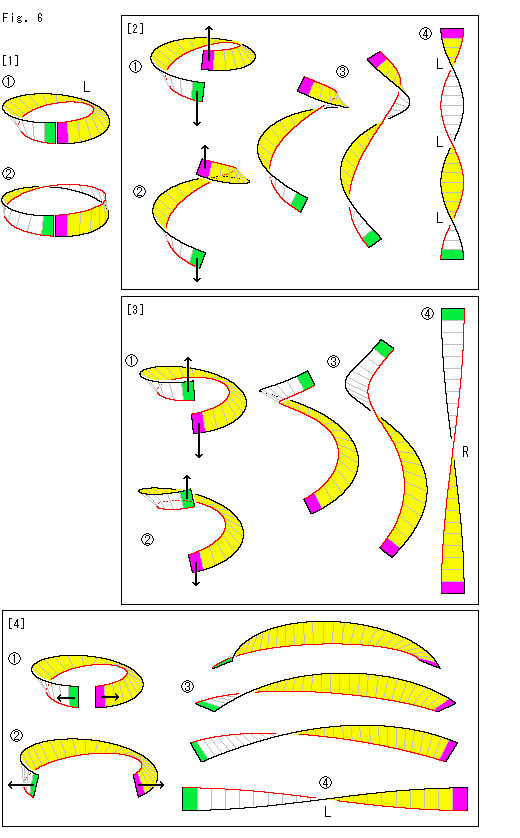
Fig.6をご覧ください。
[1]: 左捻りLのメビウスの帯の輪を切断したものです。 切断すると表裏のあるものになるので、面と縁を色分けしています。 切った端は、Fig.4のように同じ側の面ではありません。 それで、端の色をこれまでとすこし変えています。  は標準的なメビウスの帯です。 その赤い縁と黒い縁の長さは大きく異なります。
は標準的なメビウスの帯です。 その赤い縁と黒い縁の長さは大きく異なります。 のように歪めて、長さをそろえてもよいのですが、
のように歪めて、長さをそろえてもよいのですが、 のままで引っ張って、最後で整形します。 以下も同様です。
のままで引っ張って、最後で整形します。 以下も同様です。
[2]:  のように上下に引っ張っていくと、
のように上下に引っ張っていくと、 ,
, のようになり、最後は
のようになり、最後は のようになります。 図では[1]の赤い縁と黒い縁の長さが違いますが、実際に紙で作ったメビウスの帯には内側と外側の長さの違いはありません。
のようになります。 図では[1]の赤い縁と黒い縁の長さが違いますが、実際に紙で作ったメビウスの帯には内側と外側の長さの違いはありません。  ではゴムのように整形したものだと見てください。 以下でも同様です。
ではゴムのように整形したものだと見てください。 以下でも同様です。
Lが3つの540 も捻じれた短冊になっています。 もとからあったメビウスの帯のLに、上下に引っ張ったことによる2つのLが加わって
も捻じれた短冊になっています。 もとからあったメビウスの帯のLに、上下に引っ張ったことによる2つのLが加わって
L + L x 2 = L x 3
となったのです。
[3]: こんどは緑色の端を上へ、赤色の端を下へ引っ張ります。 その結果は、 のようになり、[2]から予想される通りです。
のようになり、[2]から予想される通りです。
つまり、
L + R x 2 = (L + R) + R = R
となったのです。
[4]:  のように左右に引き離していきます。
のように左右に引き離していきます。  ,
, ときて、最後の
ときて、最後の ではLが1つの短冊になっています。 この場合、リングをすぼめる引っ張りではないので、新たな捻れの出現はありません。
ではLが1つの短冊になっています。 この場合、リングをすぼめる引っ張りではないので、新たな捻れの出現はありません。
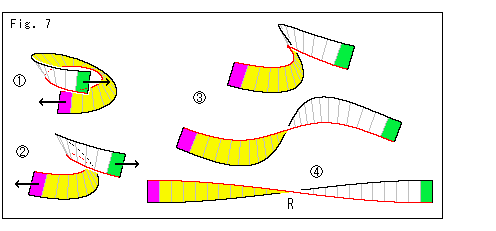
Fig.7をご覧ください。
もう見ればわかるので、説明は省きます。
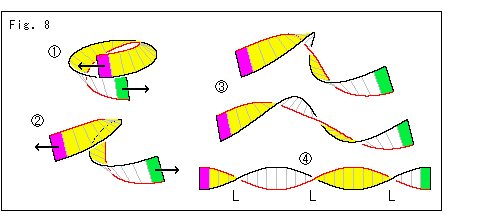
Fig.8をご覧ください。
これも見ればわかるので、説明は省きます。
メビウスの帯を切って引張ったときのセンターラインの捩れの変化は、円筒のそれとまったく同じです。 切って引張ったメビウスの帯の捩れは、もとのメビウスの帯の捩れにそのセンターラインの捩れを加えたものです。 つまり、メビウスの帯に新たに生じる捩れがセンターラインの捩れであるわけです。
日常的に帯状のものの捻れというのは、その面を這っていくときの刻々の進行方向を軸とする微小回転の合計です。 "捻れ"をこう捉えたものだけに注目すると、メビウスの帯の面を這って1周したときの捻れは180 です。 しかし実際には、メビウスの帯は1つの輪になっているので、その分の捻れもあります。 これが、事をややこしくしているわけですね。
です。 しかし実際には、メビウスの帯は1つの輪になっているので、その分の捻れもあります。 これが、事をややこしくしているわけですね。
Fig.9をご覧ください。
いきなり微分幾何のようにするのではなく、日常的な感覚に沿うことからすすめてみます。
[1]: Zはメビウスの帯の輪の中心を垂直に通っている軸です。 いま1点tがメビウスの帯上を水色の線のように点t'の方へ動いているとします。 tt'はセンタライン上でなくてもかまいません。 点tの動きとともに、tの近くの面は進行方向tPの周りに赤い矢印のようにいくらか回転します。 同時に、tの近くの面はZ軸に平行なtVを軸として緑色の矢印のようにもいくらか回転します。 この2つの回転を合成したものを全部集めれば、メビウスの帯の真の捻れにが得られます。 もっとも、「真の」というのは、メビウスの帯を外から眺めてのことです。 自転する地球を太陽を含めて見た場合に相当します。 その場合、地球は1年間に本当は365+1回自転しているのですが、地球上にいる人間から見ると365回しか自転していないのです。
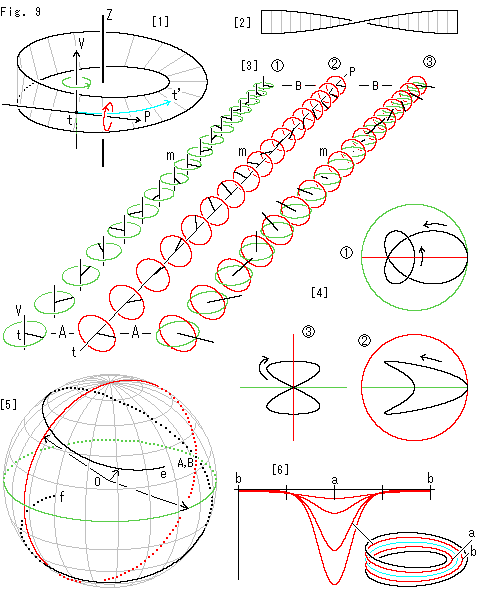 [2]: メビウスの帯の輪を切って、そのまま開いたところです。 こうすると、メビウスの帯の輪が解かれて、進行方向の捻れ180
[2]: メビウスの帯の輪を切って、そのまま開いたところです。 こうすると、メビウスの帯の輪が解かれて、進行方向の捻れ180 だけになります。 つまり、メビウスの帯上にとどまって見たときの捩れしか見えません。
だけになります。 つまり、メビウスの帯上にとどまって見たときの捩れしか見えません。
いいかえると、本当は
メビウスの帯は 180
 360
360 捩れている
捩れている
のです。 記号 は異なる方向の捩れの合成を表しています。
は異なる方向の捩れの合成を表しています。
[3]:  と
と は、メビウスの帯の反対側の面も含めて2周した分の進行方向を真っ直ぐにして、tVの周りの回転とtPの周りの回転を動径で表現したものです。 Amが1周めで、mBが2周めです。 A,m,Bはメビウスの帯上の同じところです。 すべての動径の大きさを一定にしています。 動径の大きさには意味がないからです。
は、メビウスの帯の反対側の面も含めて2周した分の進行方向を真っ直ぐにして、tVの周りの回転とtPの周りの回転を動径で表現したものです。 Amが1周めで、mBが2周めです。 A,m,Bはメビウスの帯上の同じところです。 すべての動径の大きさを一定にしています。 動径の大きさには意味がないからです。  のベクトルがtVを軸として2回転すると、
のベクトルがtVを軸として2回転すると、 のベクトルがtPを軸として1回転します。
のベクトルがtPを軸として1回転します。
 は、
は、 ,
, の動径をベクトルとみて合成してみたものです。 mのところでは合成ベクトルの大きさがゼロになっています。
の動径をベクトルとみて合成してみたものです。 mのところでは合成ベクトルの大きさがゼロになっています。
この動径の合成が当を得たものかどうかわかりませんが、ともかくつづけます。
[4]: 緑色と赤色の円を全部重ねて、合成ベクトルの先端の軌跡を描いてみました。  は真上から見たもので、
は真上から見たもので、 は真正面から見たものです。 右端から出発して矢印のように動きます。
は真正面から見たものです。 右端から出発して矢印のように動きます。  は、
は、 を真左から見たものです。
を真左から見たものです。
[5]: 各ベクトルの固定点を集めて、ガウスの球面表示とよばれているものを利用しました。 ガウスの球面表示は空間曲線の接ベクトルを採るのがふつうですが、ここでは[3]の3つのベクトルを表示しています。 3本の矢線は各ベクトルの一組の例です。 黒い曲線が合成ベクトルの動きです。 その端点e,fは、球面Oの対心点になっていて、[3]のmのところでeからfへジャンプします。
描いてはみたものの、こんな図では、どこがどう捩れているのかさっぱりわかりませんね。
[6]: メビウスの帯のセンターラインから一定距離の曲線の曲率です。(曲率曲線ではありません。)全域にわたりマイナスになっていて、センターラインからの距離が大きいほどグラフが窪んでいます。 メビウスの帯の内側a付近で曲率が負の最大になっています。 b付近では、ほとんどゼロです。 このグラフは縦軸を100倍に拡大して描いてあります。 そうしないと、グラフのカーブがよく見えないからです。
紙で作ったメビウスの帯は四方八方公平に曲がっているので、グラフがこんな風にはならないはずです。 たぶん、水平な直線になるでしよう。 しかし、紙で作ったメビウスの帯においても、[3],[4]に変わりはないに違いありません。(私たちは、紙製メビウスの帯を表す式をいまだに見出していないので、残念ながら立証してお見せすることができません。)
こうしてみると、[3]の までの考えに留めておくのがよいと思われます。 微分幾何の真似をしても得るところはありませんね。 とはいえ、球面表示はとても示唆に富んでいます。 何かがつかめそうな気がします。(微分幾何には曲面の捩率といったものはありません。 あるのは曲率だけです。)
までの考えに留めておくのがよいと思われます。 微分幾何の真似をしても得るところはありませんね。 とはいえ、球面表示はとても示唆に富んでいます。 何かがつかめそうな気がします。(微分幾何には曲面の捩率といったものはありません。 あるのは曲率だけです。)
それにしても、360 の回転というのは魔術的ですね。 変化があるのに、すべてを元に戻して、何もなかった顔をするのですから。
の回転というのは魔術的ですね。 変化があるのに、すべてを元に戻して、何もなかった顔をするのですから。
**************************************************
それでは、Fig.2の白い帯の捻じれ具合いを調べます。
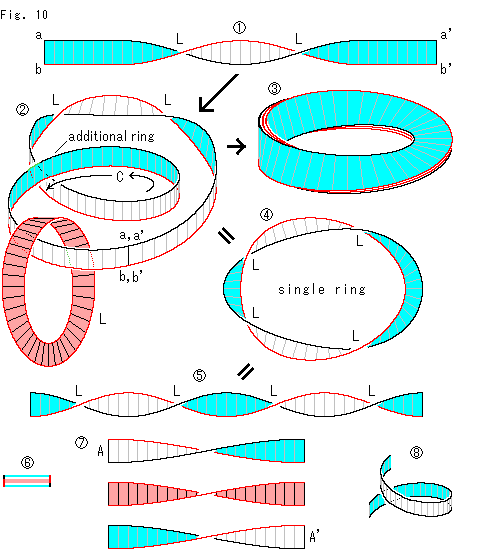
Fig.10をご覧ください。
 : 360
: 360 捻じた短冊です。 これをメビウスの帯の全面に沿わせて、
捻じた短冊です。 これをメビウスの帯の全面に沿わせて、 を得ようとします。
を得ようとします。
 : そのために、Cのように巻いて1つの輪(additional ring)を加えてから両端を継なぎます。 その際、新たな捻りを加えることはしません。
: そのために、Cのように巻いて1つの輪(additional ring)を加えてから両端を継なぎます。 その際、新たな捻りを加えることはしません。
 : 出来上がって3層になっているメビウスの帯です。 層の数は、数え方によっては2層ですね。
: 出来上がって3層になっているメビウスの帯です。 層の数は、数え方によっては2層ですね。
 :
:  の2つのリングの帯をほぐして1つのリング(single ring)にしたところです。 もとの2つのLに新たに現れた2つのLが加わって、360
の2つのリングの帯をほぐして1つのリング(single ring)にしたところです。 もとの2つのLに新たに現れた2つのLが加わって、360 x2 の捻れになっています。
x2 の捻れになっています。
 :
:  を切って、そのままで真っ直ぐに開いたものです。
を切って、そのままで真っ直ぐに開いたものです。  と
と とは、明らかに同じではありません。 Fig.9では、切って開いたものの捩れがメビウスの帯上の住人の見る捩れになっていました。 それは、切り開くことによって、メビウスの帯の輪が解かれたからでした。
とは、明らかに同じではありません。 Fig.9では、切って開いたものの捩れがメビウスの帯上の住人の見る捩れになっていました。 それは、切り開くことによって、メビウスの帯の輪が解かれたからでした。
しかし、ここで切り開いたのは、 であって、
であって、 ではありません。 切って捩れを見ようとするのなら、
ではありません。 切って捩れを見ようとするのなら、 を切るべきですね。
を切るべきですね。
 : 3層になっているメビウスの帯
: 3層になっているメビウスの帯 を切った断面です。 面に厚みをつけて描いています。 水色の面が180
を切った断面です。 面に厚みをつけて描いています。 水色の面が180 回転して上下が逆になっていることに注意してください。 この
回転して上下が逆になっていることに注意してください。 この の外層には表裏がありますが、縁を除いた外観は水色一色です。
の外層には表裏がありますが、縁を除いた外観は水色一色です。
 : 切ってできた3つの捻れた短冊です。 このうちのAとA'を継なげば、もとの
: 切ってできた3つの捻れた短冊です。 このうちのAとA'を継なげば、もとの が得られます。
が得られます。
 : ちょっと注意が必要です。 帯を巻いてリングをつくるときは、
: ちょっと注意が必要です。 帯を巻いてリングをつくるときは、 のCのように立体交差の上側をまたがせねばなりません。 そうしないで、この
のCのように立体交差の上側をまたがせねばなりません。 そうしないで、この のように下側をくぐらせると、メビウスの帯に密着させることができなくなります。 Rが2つ生まれて、もとの2つのLとキャンセルし合って、まったく捻れのないものになってしまうからです。
のように下側をくぐらせると、メビウスの帯に密着させることができなくなります。 Rが2つ生まれて、もとの2つのLとキャンセルし合って、まったく捻れのないものになってしまうからです。
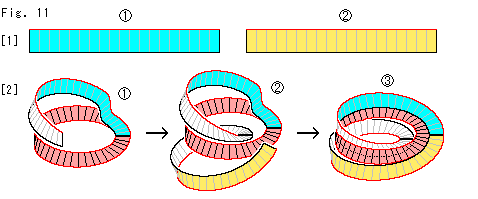 Fig.11をご覧ください。
Fig.11をご覧ください。
[1]: 上のFig.10では、はじめに捩じた短冊を用意しましたが、短冊はやわらかいので、捩じていないものをメビウスの帯の面に張っていっても、ひとりでに3層のメビウスの帯が得られます。 2つの短冊 ,
, は、それを確かめるためのものです。 長いもの1つで足りるのですが、図解の便のために短いもの2つを用意したのです。
は、それを確かめるためのものです。 長いもの1つで足りるのですが、図解の便のために短いもの2つを用意したのです。
[2]: まず、捩れていない短冊の1つを のようにメビウスの帯に張っていきます。 短冊はやわらかいので、メビウスの帯の面にぴったりと沿います。 つづけて
のようにメビウスの帯に張っていきます。 短冊はやわらかいので、メビウスの帯の面にぴったりと沿います。 つづけて のように、もう1つを張ります。 すると、内側に白い面が見えているように新しいリングがひとりでにできます。 そして最後の端を張りおわると
のように、もう1つを張ります。 すると、内側に白い面が見えているように新しいリングがひとりでにできます。 そして最後の端を張りおわると のようになって、さらにリングができます。 張るという工程でリングが2つと180
のようになって、さらにリングができます。 張るという工程でリングが2つと180 の捩れが2つ加わったのです。 加えられた捩れは、合計
の捩れが2つ加わったのです。 加えられた捩れは、合計
360 x 2
x 2  180
180 x 2
x 2
です。 記号 はFig.9の話しにあるのと同じです。 その "
はFig.9の話しにあるのと同じです。 その " " を "+" にしてみると、360
" を "+" にしてみると、360 の2倍どころか3倍にもなるではありませんか!
の2倍どころか3倍にもなるではありませんか!
これで、「なぜ、そんなに捻れるのか」の疑問が解明されました。
要するに、リングをつくれば、その数だけの360 の捩れが内在的に生まれるということですね。 そして、リングをこれまでに見てきたように変形すると、その捩れが顕在化するわけです。
の捩れが内在的に生まれるということですね。 そして、リングをこれまでに見てきたように変形すると、その捩れが顕在化するわけです。
ところで、表裏の有無とは別に、「反対側の面」とか「全面」といったことばをときどきつかっています。 面に表裏があってもなくても、面上の1点などというとき、その点が面のどちらの側にあるかを問題にすることはありません。 数学的な面には厚さがないのですから、当然です。 しかし、私たちが「反対側の面」などといっているときは、面を不透明な紙のようなものと考えています。 そうでないと、メビウスの帯の面を挟む話ができないからです。 この点、混乱しないようにしてください。
**************************************************
クロスキャップの紙細工です。
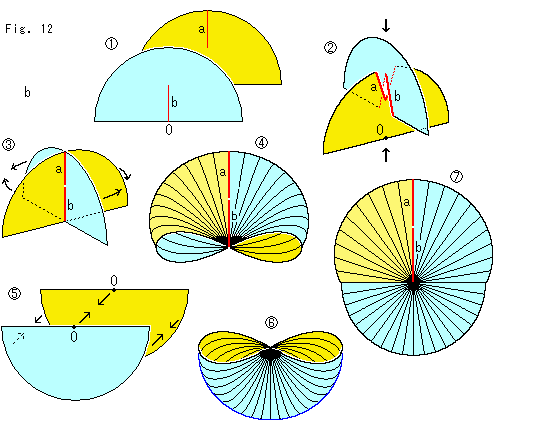 Fig.12をご覧ください。
Fig.12をご覧ください。
 : 半円の紙2枚をつかをつかって、クロスキャップの頭部をつくります。 赤い線a,bのように切り込みを入れます。 Oは半円の中心で、a,bはともに半径の1/2です。
: 半円の紙2枚をつかをつかって、クロスキャップの頭部をつくります。 赤い線a,bのように切り込みを入れます。 Oは半円の中心で、a,bはともに半径の1/2です。
 : aとbの切り込みを十字にかみ合わせます。
: aとbの切り込みを十字にかみ合わせます。
 : きっちり押し込んでから、半円の周と周を矢印のように貼り合わせます。
: きっちり押し込んでから、半円の周と周を矢印のように貼り合わせます。
 : そして内側を膨らませると、できあがります。 下の方がすぼんでいますが、そうならないようにするには、半円でなく横長の半楕円にした紙をつかうとうまくいきます。
: そして内側を膨らませると、できあがります。 下の方がすぼんでいますが、そうならないようにするには、半円でなく横長の半楕円にした紙をつかうとうまくいきます。
 : つぎに、クロスキャップの下部をつくります。
: つぎに、クロスキャップの下部をつくります。  と同じ大きさの切り込みのない半円の周と周、中心と中心を貼り合わせます。
と同じ大きさの切り込みのない半円の周と周、中心と中心を貼り合わせます。
 : そして内側を膨らませると、できあがります。 これを
: そして内側を膨らませると、できあがります。 これを とドッキングさせると、クロスキャップ全体になります。 ドッキングの前に詰め物を何か入れておくとよいでしよう。 しかし、ドッキングしないで内側が覗ける方が都合がよいですね。
とドッキングさせると、クロスキャップ全体になります。 ドッキングの前に詰め物を何か入れておくとよいでしよう。 しかし、ドッキングしないで内側が覗ける方が都合がよいですね。
クロスキャップの形だけなら縦に分割しても作れますが、それでは自己交差のところをそれらしくすることができません。 紙の面が連続して自己交差の交線を通過しないからです。
 : 完成したクロスキャップを真正面から見たものです。 変な彩色になっているのは、表裏のある紙を使ったからです。
: 完成したクロスキャップを真正面から見たものです。 変な彩色になっているのは、表裏のある紙を使ったからです。
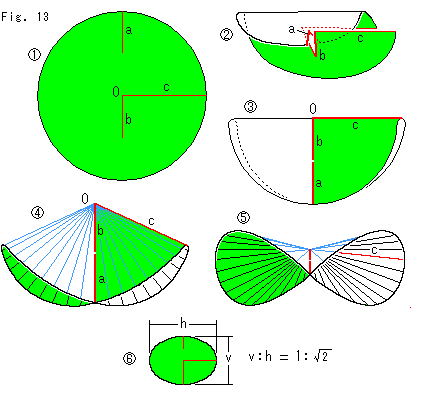 Fig.13をご覧ください。
Fig.13をご覧ください。
1枚の紙でクロスキャップの頭部をつくります。
 : 円形の紙に赤い線aとbOcのように切り込みを入れます。 円の中心がOで、bOcは直角です。 a,bは同一の直径上にあって、長さはともに半径の1/2です。
: 円形の紙に赤い線aとbOcのように切り込みを入れます。 円の中心がOで、bOcは直角です。 a,bは同一の直径上にあって、長さはともに半径の1/2です。
 : bOcを前後に開きます。 そして、aをこちら側へ曲げてbと噛み合わせます。
: bOcを前後に開きます。 そして、aをこちら側へ曲げてbと噛み合わせます。
 : a,bをきっちり押し込んでから、cを閉じ戻します。
: a,bをきっちり押し込んでから、cを閉じ戻します。
 : 左右の内側を広げたところです。 これで、出来上がりです。
: 左右の内側を広げたところです。 これで、出来上がりです。
2つの円錐を、頂点を合わせてくっつければ、これと似たものが得られます。 しかし、そうしたのでは自己交差のところが連続した面の交差にはなりせん。
 : 下の方から見たものです。
: 下の方から見たものです。
 : 広げた裾を水平にするなら、図のような楕円の紙をつかえばできます。 しかし、上端はやはり尖ったままになります。 尖らないようにするには長方形の紙をつかえばよいのですが、それだとホワイト二ーの傘なってしまいます。
: 広げた裾を水平にするなら、図のような楕円の紙をつかえばできます。 しかし、上端はやはり尖ったままになります。 尖らないようにするには長方形の紙をつかえばよいのですが、それだとホワイト二ーの傘なってしまいます。
この紙のクロスキャップの自己交差の交線上に向こう側へ貫通したスロットを開けてしておくと便利です。 そのスロットにやわらかいテープを通して、メビウスの帯との関係を観察したりすることができす。
 メビウスの帯の縁を底辺とした錐面をつくります。 錐面は2重になり、自己交差します。
メビウスの帯の縁を底辺とした錐面をつくります。 錐面は2重になり、自己交差します。
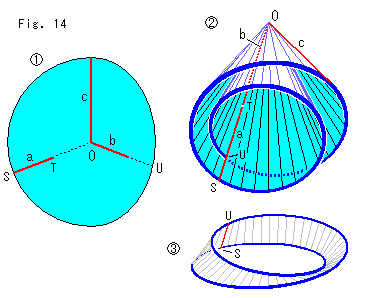
Fig.14をご覧ください。
 : こんどは、左半分が円で、右半分が楕円の紙に赤い切り込みaとbOcを入れます。 aとbの傾きはcに関してほぼ対称にとり、aの右端Tから中心Oまでの距離をbの長さと等しくします。
: こんどは、左半分が円で、右半分が楕円の紙に赤い切り込みaとbOcを入れます。 aとbの傾きはcに関してほぼ対称にとり、aの右端Tから中心Oまでの距離をbの長さと等しくします。
 : Fig.14と同じ要領でaとbを噛み合わせます。 そして、できた錘を囲むようにcを継なぎ戻します。 UOが自己交差になっているところです。
: Fig.14と同じ要領でaとbを噛み合わせます。 そして、できた錘を囲むようにcを継なぎ戻します。 UOが自己交差になっているところです。
 : 錐面
: 錐面 に対応するメビウスの帯です。 この場合、メビウスの帯は錐面の底にぴったり接合します。
に対応するメビウスの帯です。 この場合、メビウスの帯は錐面の底にぴったり接合します。
 Fig.15をご覧ください。
Fig.15をご覧ください。
前章で作ったクロスキャップの紙細工します。
[1]: いくつかのだ円を、縦軸を共有して水平に回る水車の羽根のように組みます。 だ円の横径dはすべて等しくとります。 一番小さいだ円(=円)の回転角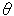 をゼロにとって上から見ると、
をゼロにとって上から見ると、 のようになります。 縦径Dは、グラフ
のようになります。 縦径Dは、グラフ のように
のように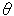 にあわせて大きくします。
にあわせて大きくします。
全体の縦横の比は、もちろん好みに合わせて変えてもかまいません。
[2]: 完成品です。 ちょっと傾けて、上の方から見ると のようになっており、下から底部を見ると
のようになっており、下から底部を見ると のようになっています。
のようになっています。
下のFig.16をご覧ください。
このクロスキャップを実際に作るのは簡単です。 左上の図のように全体の1/4を作って継なぎます。 下に並べてある形に紙を切ったものを4組用意します。 それらを縦に折り、同じ半楕円どうしを貼っていきます。 この絵を印刷して、使ってみてください。 (左上の図では、こいピンクとうすいピンクの面が交互に見えていますが、つづけて貼っていくと同じ色がつづいたり、紙の裏側になったりします。 ですから、無色にした方が無難です。)
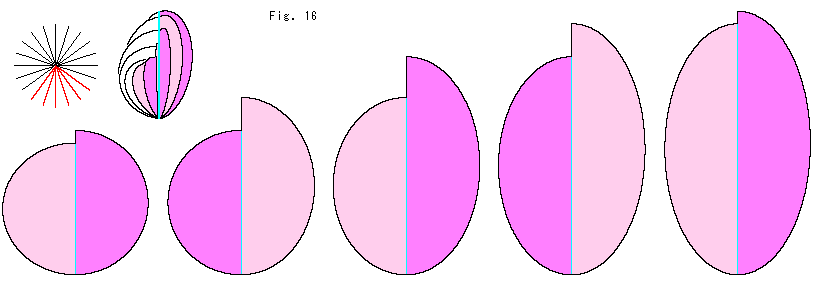
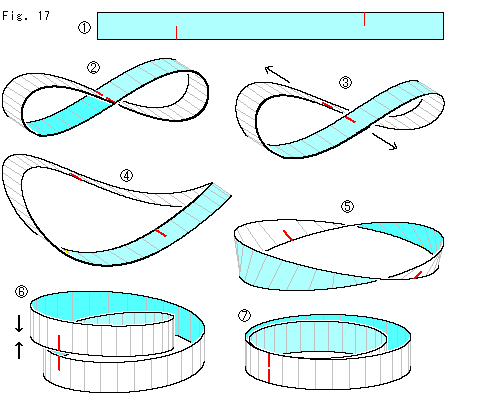 Fig.17をご覧ください。
Fig.17をご覧ください。
クロスキャップの頭部を輪切りした8字形の面から細工します。
 : 短冊に赤い線のように2つの切り込みを入れます。
: 短冊に赤い線のように2つの切り込みを入れます。
 : 切り込みと切り込みを咬み合わせてから、両端を(捻じらないで)継いで8字形にします。 これを出発点に考えます。
: 切り込みと切り込みを咬み合わせてから、両端を(捻じらないで)継いで8字形にします。 これを出発点に考えます。
 : 8字形の面の捻じれを見るために、あらためて咬み合っているところを矢印のように引き離します。
: 8字形の面の捻じれを見るために、あらためて咬み合っているところを矢印のように引き離します。
 : さらに引き離したところです。
: さらに引き離したところです。
 : ほぐしてみると、360
: ほぐしてみると、360 捻じれたループになっていることがわかります。 これは、クロスキャップの自己交差の交線のある面は、360
捻じれたループになっていることがわかります。 これは、クロスキャップの自己交差の交線のある面は、360 捻じれているということです。
捻じれているということです。  で咬み合わせを外していますが、捻じれに変わりはありません。 咬み合わせを抜いたり刺したりしても、切断してはいないからです。
で咬み合わせを外していますが、捻じれに変わりはありません。 咬み合わせを抜いたり刺したりしても、切断してはいないからです。
 : 図のようにくるまったところでは、紙の同じ面が同じ側にきています。 こうなったところで、上下から切り込みをふたたび咬み合わせて押し込みます。
: 図のようにくるまったところでは、紙の同じ面が同じ側にきています。 こうなったところで、上下から切り込みをふたたび咬み合わせて押し込みます。
 : できたものは、Fig.14の錐面を輪切りしたものと同じ構造になっています。 これは、
: できたものは、Fig.14の錐面を輪切りしたものと同じ構造になっています。 これは、 のように咬み合っているところを抜かなくても、8字形
のように咬み合っているところを抜かなくても、8字形 の一方のループを裏返すように捻ねって他方のループに重ねるようにすれば、できます。
の一方のループを裏返すように捻ねって他方のループに重ねるようにすれば、できます。
**************************************************
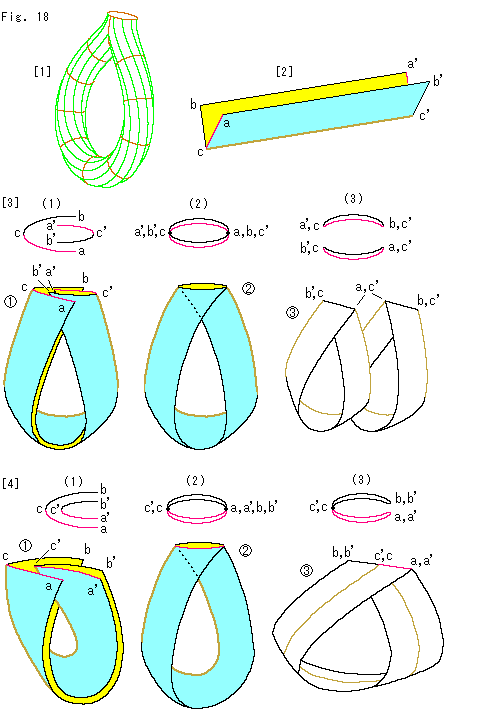
Fig.18をご覧ください。
クラインの壷から得られるメビウスの帯は、切り方によって1つになったり2つになったりするのを見ましてが、それを紙細工でやってみます
[1]: チューブでつくったクラインの壷です。 この対称的な形のクラインの壷を紙で作り、それを切ります。
[2]: 短冊を図のように折ります。 端のacとa'c'を赤くし、折り目cc'を茶色に塗ってあるのは、これからのイラストのためです。
[3]: 一方の端を他方に咬ませて のようにします。 上から見ると、(1)のようになっています。 きっちり押し込み(2)のようにして、acとb'c'を継なぎ、a'c'とbcを継なぎます。 そして、長い縁ab'とa'bを
のようにします。 上から見ると、(1)のようになっています。 きっちり押し込み(2)のようにして、acとb'c'を継なぎ、a'c'とbcを継なぎます。 そして、長い縁ab'とa'bを のようにできる範囲で継ないでいきます。 それができない上の方は自己交差になっているところです。 これで[1]と同じクラインの壷ができました。
のようにできる範囲で継ないでいきます。 それができない上の方は自己交差になっているところです。 これで[1]と同じクラインの壷ができました。
できたクラインの壷をもとの短冊の茶色の折り目cc'に沿って切ります。 すると、左捻りと右捻りの2つのメビウスの帯 ができます。
ができます。  の上端は(3)のように真っ二つになっています。
の上端は(3)のように真っ二つになっています。
[4]: こんどは、折った短冊の端の一方を他方に のように差し込みます。 (1),(2),(3)は上端を上から見たものです。 きっちり押し込んで、acとa'c'を継なぎ、bcとb'c'を継なぎます。 そして[3]と同様に、長い縁ab'とa'bを継ないでいきます。 すると、これも[1]と同じクラインの壷になりました。 [3]のクラインの壷と異なるように見えますが、クラインの壷としては変わりありません。
のように差し込みます。 (1),(2),(3)は上端を上から見たものです。 きっちり押し込んで、acとa'c'を継なぎ、bcとb'c'を継なぎます。 そして[3]と同様に、長い縁ab'とa'bを継ないでいきます。 すると、これも[1]と同じクラインの壷になりました。 [3]のクラインの壷と異なるように見えますが、クラインの壷としては変わりありません。
こうしてできたクラインの壷の、いま継ないだばかしの縁ab'とa'bを切り離します。 (3)で見ると、U字形に切られています。 短冊の折り目であったcc'に沿って開いていきます。 すると、巾の広い1つのメビウスの帯 が得られます。 このメビウスの帯は左捻りですが、
が得られます。 このメビウスの帯は左捻りですが、 で端と端の差し込みの内外を逆にすると、右捻りになります。
で端と端の差し込みの内外を逆にすると、右捻りになります。
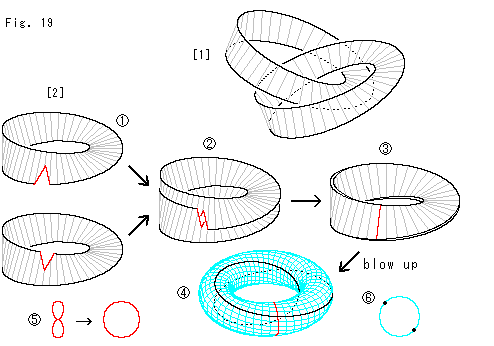 Fig.19をご覧ください。
Fig.19をご覧ください。
捻れが逆の2つのメビウスの帯の縁と縁を貼り合わせるとクラインの壷になりますが、捻れが同じ向きの2つのメビウスの帯の縁と縁を貼り合わせると捻れたトーラスになるといわれています。 紙細工でそれにはを工夫してみます。
[1]: 2つのメビウスの帯を重ねることは、ふつうには不可能です。 図のように絡めておいても、うまくいきません。
[2]: そこで、メビウスの帯に のように切り込み入れます。 そして、
のように切り込み入れます。 そして、 のように咬み合わせます。 しっかり押し込んで切り込みを閉じると、
のように咬み合わせます。 しっかり押し込んで切り込みを閉じると、 のように面と面が向かい合います。 このとき、赤い切り込みの線は自己交差の交線になっています。 面と面はくっつけないで、縁と縁だけを貼り合わせために膨らませる(blow up)と、面が捻れたトーラス
のように面と面が向かい合います。 このとき、赤い切り込みの線は自己交差の交線になっています。 面と面はくっつけないで、縁と縁だけを貼り合わせために膨らませる(blow up)と、面が捻れたトーラス になります。 ただし、切り込みであった赤いところは、8字形になっていたのを
になります。 ただし、切り込みであった赤いところは、8字形になっていたのを のように強引に丸くしてのことです。 つまり、自己交差であったことを無視しています。 そして、このトーラスは、場所ごとに見て黒い線のように仕切られており、2つのメビウスの帯が断面
のように強引に丸くしてのことです。 つまり、自己交差であったことを無視しています。 そして、このトーラスは、場所ごとに見て黒い線のように仕切られており、2つのメビウスの帯が断面 のように貼り合わされいるのだと考えるのです。
のように貼り合わされいるのだと考えるのです。
もっとも、出来上がってしまったトーラスには赤いリングや黒い仕切り線を残しておく必要はありません。
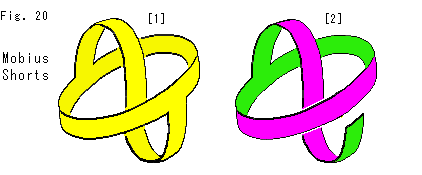 ヘンな紙細工を見ておきます。
ヘンな紙細工を見ておきます。
Fig.20をご覧ください。
[1]: メビウスのパンツ(Mobius shotrs)とよばれている表裏のないものです。 この面は、捻られているのでしようか、それとも?
[2]: 色を塗っていけば、表裏のないことがはっきりします。 図は、切断してから色を塗って、表裏を色分けしたものです。 S字形になっているところは、いわば表裏をつなぐバイパスです。 これを紙細工するするには、どのように紙を切ればよいでしようか。 細工する前に考えてみてください。
さて、[1]の紙細工を切ったり色を塗ったりしないで捻じれを確かめるには、どうにほぐせばよいでしようか。 どんなにいじくっても、1つのループにはなりません。
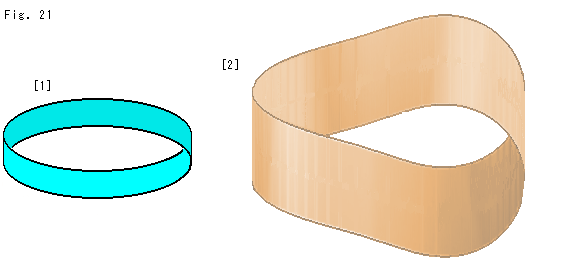 Fig.21をご覧ください。
Fig.21をご覧ください。
[1]: このループは表裏のないものに見えまませんか。 ぐるっとループ上を目で追ってみてください。 メビウスの帯でしようか?
これを紙細工することは絶対に不可能です。 この絵は、だまし絵の一つですが、考えさせられますね。
[2]: これはどうでしようか。 目をほそめて追っていくと、なんだかおかしいですね。 これは騙し絵ではありません。 360 捻じれた普通のベルトです。 でも、ヘンに見えたり、まともに見えたりするのは、なぜでしようか。 視線をシャープにしてベルトの上を追っていったときと、全体を一度に見たときは違った感じになりますね。よく観察してみてください。
捻じれた普通のベルトです。 でも、ヘンに見えたり、まともに見えたりするのは、なぜでしようか。 視線をシャープにしてベルトの上を追っていったときと、全体を一度に見たときは違った感じになりますね。よく観察してみてください。
人間の3次元を認識する力なんて、弱いものですよ。
紙細工はこれくらいにして、射影幾何にもどりましよう。
[前章] [次章] [目次]


 Fig.3をご覧ください。
Fig.3をご覧ください。

 ということがわかりました。
ということがわかりました。 Fig.5をご覧ください。
Fig.5をご覧ください。


 [2]: メビウスの帯の輪を切って、そのまま開いたところです。 こうすると、メビウスの帯の輪が解かれて、進行方向の捻れ180
[2]: メビウスの帯の輪を切って、そのまま開いたところです。 こうすると、メビウスの帯の輪が解かれて、進行方向の捻れ180
 Fig.11をご覧ください。
Fig.11をご覧ください。 Fig.12をご覧ください。
Fig.12をご覧ください。 Fig.13をご覧ください。
Fig.13をご覧ください。 メビウスの帯の縁を底辺とした錐面をつくります。 錐面は2重になり、自己交差します。
メビウスの帯の縁を底辺とした錐面をつくります。 錐面は2重になり、自己交差します。 Fig.15をご覧ください。
Fig.15をご覧ください。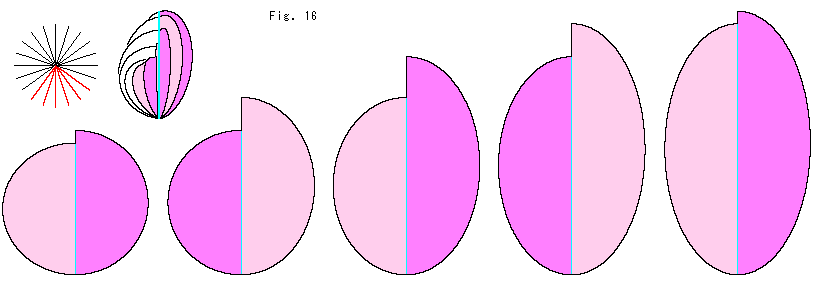
 Fig.17をご覧ください。
Fig.17をご覧ください。
 Fig.19をご覧ください。
Fig.19をご覧ください。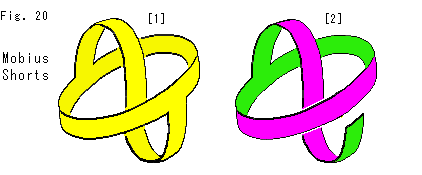 ヘンな紙細工を見ておきます。
ヘンな紙細工を見ておきます。 Fig.21をご覧ください。
Fig.21をご覧ください。