第3部 射影幾何から双曲幾何へ
Ch.45 射影幾何 (3) 
射影平面からクラインの円板モデルを作ります。 クラインが発見した方法と同じではありませんが、彼の基本的な考え方にならいます。
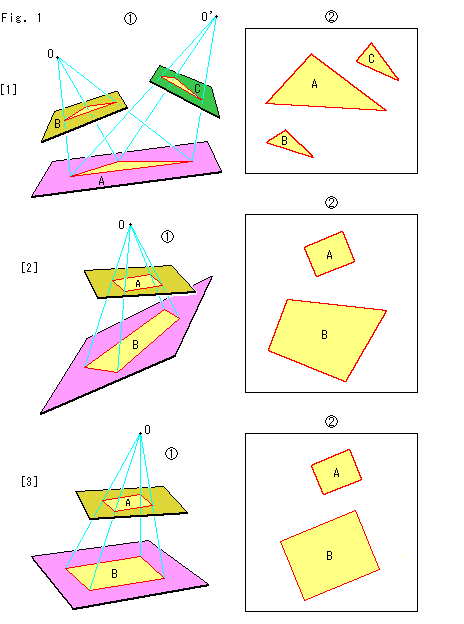
Fig.1をご覧ください。
[1]: 1つの三角形を2つの異なる平面へ射影してみます。
 は、下にあるピンク色の平面上の三角形Aを別の黄色と緑色の2つの平面へ射影して、三角形Bと三角形Cを得たところです。 射影の中心Oから見て、三角形AとBは同じです。 射影の中心O'から見れば、三角形AとCが同じです。 三角形BとCも射影的に同じですが、両者のための1つの射影の中心が見出せません。 1つの射影の中心で図形を動かすことを配景変換といいます("背景"ではありません)。 三角形Bを三角形Cへ移すには、一度ピンク色の平面上の三角形Aに移して(BをAに変えて)、それを三角形Cへ移すことになります。
は、下にあるピンク色の平面上の三角形Aを別の黄色と緑色の2つの平面へ射影して、三角形Bと三角形Cを得たところです。 射影の中心Oから見て、三角形AとBは同じです。 射影の中心O'から見れば、三角形AとCが同じです。 三角形BとCも射影的に同じですが、両者のための1つの射影の中心が見出せません。 1つの射影の中心で図形を動かすことを配景変換といいます("背景"ではありません)。 三角形Bを三角形Cへ移すには、一度ピンク色の平面上の三角形Aに移して(BをAに変えて)、それを三角形Cへ移すことになります。
 は、3つの三角形A,B,Cを同一の平面上に置いたものです。 このような一つの平面上で、三角形Bを三角形Cへ直接移すことも含めた変換を射影変換といいます。 射影変換には、配景変換も含まれています。 射影の中心を変えた配景変換を何度かすると、射影変換になります。 変換とは、図形でいえば、その動かし方です。 射影変換は、点を点に、直線を直線に、2次曲線を2次曲線に換えるものです。
は、3つの三角形A,B,Cを同一の平面上に置いたものです。 このような一つの平面上で、三角形Bを三角形Cへ直接移すことも含めた変換を射影変換といいます。 射影変換には、配景変換も含まれています。 射影の中心を変えた配景変換を何度かすると、射影変換になります。 変換とは、図形でいえば、その動かし方です。 射影変換は、点を点に、直線を直線に、2次曲線を2次曲線に換えるものです。
[2]: 射影で長方形はどう変わるでしようか。 平行四辺形になると思われそうですが、そうとは限らないのです。
 のように上側の平面にある長方形Aをピンク色の平面へ射影して、四辺形Bを得ます。
のように上側の平面にある長方形Aをピンク色の平面へ射影して、四辺形Bを得ます。
 は、長方形Aと四辺形Bを同一の平面上にならべたところです。 この場合、四辺形Bのどの辺も他の辺と同じ長さではありません。
は、長方形Aと四辺形Bを同一の平面上にならべたところです。 この場合、四辺形Bのどの辺も他の辺と同じ長さではありません。
[3]: 上下の平面を平行にしてみます。
 のように射影されるのですが、ちょっと見ると、射影の中心Oが長方形Aの真上にはなく右の方にずれているので、四辺形Bの左の方が大きくなるように思えますが、そうはなりません。
のように射影されるのですが、ちょっと見ると、射影の中心Oが長方形Aの真上にはなく右の方にずれているので、四辺形Bの左の方が大きくなるように思えますが、そうはなりません。
 では、 四辺形Bが長方形Aと相似な長方形になっていることがわかります。 そして、これ以外の場合には、長方形が長方形や平行四辺形になることはありません。 つまり、原像と写像がのる平面が平行でないかぎり、四辺形Bは[2]のようになるのです。 それは、どの2辺も延長すれば、交わるということです。
では、 四辺形Bが長方形Aと相似な長方形になっていることがわかります。 そして、これ以外の場合には、長方形が長方形や平行四辺形になることはありません。 つまり、原像と写像がのる平面が平行でないかぎり、四辺形Bは[2]のようになるのです。 それは、どの2辺も延長すれば、交わるということです。
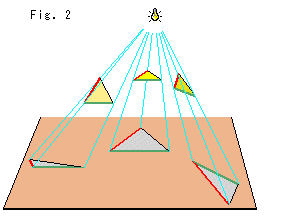
Fig.2のように、一つの三角形を光線の下で動かすと、その影はいろいろに変化して、鋭角三角形になったり鈍角三角形になったり、ときには線分にもなります。 しかし、もとの三角形に変わりはありません。 光源が1つですから、どの影の三角形も配景変換されたものになっています。 もし、この影を測って、もとの三角形を言い当てることができたら、とても好都合です。 そこで、それができるとして、どの影も合同だということにします。 Fig.1の三角形も同様な意味で、すべて合同です。 でも、計量化するまでは、合同とはいわないで、対応しているとしておくのがよいでしよう。 なにしろ、射影平面には、長さや角の概念はないのですから。
 射影変換では、点が別の場所に移るだけでなく、角や長さも変わります。 つまり、射影平面の上では、ふつうの計量がありません。 角も距離も合同も関心事ではないのです。 しかし、それでは困ります。 そこで、射影変換に条件をつけて、距離も角も定まるようにします。 そうすることを計量化といいます。
射影変換では、点が別の場所に移るだけでなく、角や長さも変わります。 つまり、射影平面の上では、ふつうの計量がありません。 角も距離も合同も関心事ではないのです。 しかし、それでは困ります。 そこで、射影変換に条件をつけて、距離も角も定まるようにします。 そうすることを計量化といいます。
さて、Fig.3のように射影平面(projective plane)の上に単位円(半径1の円)を描きます。 これを円板モデルの円にしようとするのです。
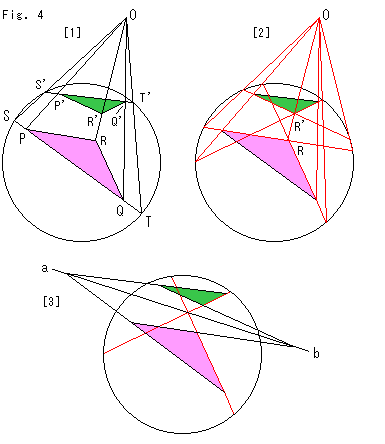 Fig.4をご覧ください。
Fig.4をご覧ください。
[1]は、円板の外側に射影の中心Oを1つとって、作図で三角形を動かしたものです。 ピンクの三角形PQRを緑色の三角形P'Q'R'へ動かします。 頂点 P', Q', R' が、それぞれ頂点 P, Q, R に対応しています。 三角形PQRを三角形P'Q'R'へ移動するには、まず辺PQを延長して弦STを描き、辺PQに対応する辺P'Q'を乗せようとする弦S'T'を引きます。 そして、点S,S'を通る直線と点T,T'を通る直線との交点O(射影の中心)を得ます。 すると、射線OPと弦S'T'の交点が点P'になり、射線OQと弦S'T'の交点が点Q'になります。
[2]は、つづけて、点Rを点R'へ移動したものです。 作図の説明は省きますが、射影の中心Oとの関係は赤い線のようになっています。
[3]の直線abは、鏡映の軸です。 ピンクの三角形と緑色の三角形は、鏡映の軸に関して一方が他方の裏返しになっています。 この鏡映が、[1][2]の操作で行われたわけです。 新たに鏡映の軸をえらんで、もう一度裏返せば表側になりますが、射影の中心も新しいところになります。
これでクラインの円板モデル上の図形の動きになっています。 Fig.4は射影の中心Oを1つだけとって動かしたもの(配景変換)ですが、円板上の図形の双曲幾何としての動きが射影的であることが歴然としています。
しかし、こんな作図ではたんに合同であることがいえるだけで、長さがわかりません。
たとえば、Fig.2の影のどれを測っても同じ結果となるようにしたい。 それには、物差しや分度器が、影とともに変化すればよいわけですね。 運よく、そんな物差しのようなものがあるのです。 それは複比とよばれるものです。 見かけは違っていても変わらない値を不変量といいます。 遠くにあるものは小さく見えます。 しかし、30cmのモノはどこにあっても30cmです。 その30という値は不変量です。 複比は、同様な意味で不変量です。 迎合的にいえば、複比がもっている不変量としての性質にあわせてモノの長さ(の測り方)を定義すればよいわけです。 つまり、複比をつかって長さを定義しようとするのです。 それが、これからの話です。
複比は、4つの数の比の比です。 4つの数のうち少なくも3つは異なるものとします。 点が並んでいるのを点列といいます。 直線上の点列S,P,Q,Tの複比の一つは、S,P,Q,Tを座標として、
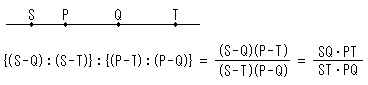
です。 SQ,PT,STなどは正負のある、いわゆる有向線分です。 ここではABと書いたときは、AB = B - A を表しているものとしておきます。 複比は、よく (SPQT) のように表わします。 つまり、
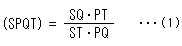
です。 複比をつくる4点S,P,Q,Tの組み合わせは、24(=4!)通りもありますが、異なる値の複比は6通りしかありません。 それは、たとえば、
(SPQT) = (PSTQ) = (QTSP) = (TQPS)
といった組があるからです。
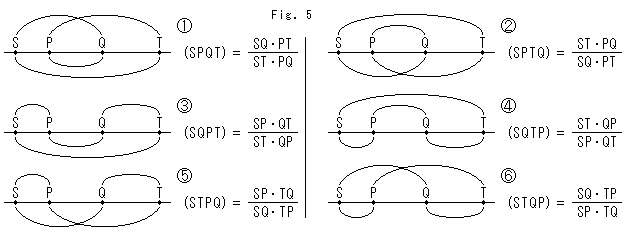
 上のFig.5は、値を異にする複比のリストです。 各複比は、同じ値の4つの複比を1つで代表しています。 それぞれの組み合わせ図の上側は分子で、下側は分母です。 左の列の
上のFig.5は、値を異にする複比のリストです。 各複比は、同じ値の4つの複比を1つで代表しています。 それぞれの組み合わせ図の上側は分子で、下側は分母です。 左の列の ,
, ,
, と右の列の
と右の列の ,
, ,
, は、それぞれ逆数関係になっているだけなので、実質3通りです。 どの複比もすべて、射影変換で変わることはありません。
は、それぞれ逆数関係になっているだけなので、実質3通りです。 どの複比もすべて、射影変換で変わることはありません。
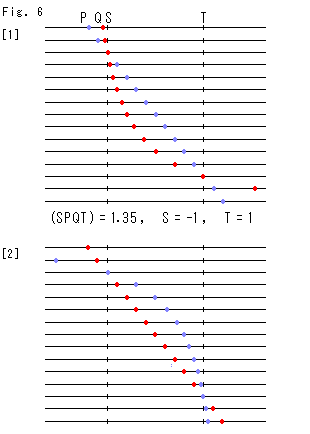
Fig.6は、複比(SPQT)の値を一定にしたときの点Pと点Qがとり得る位置関係です。 直線を並べておいて、各直線に2点P,Qの位置をプロットしています。 2点S,Tは固定されています。
[1]: 青い点Pを等間隔に動かして、複比(SPQT)の値が変わらないように赤い点Qを追従させたものです。 左上を見ると、点Pが点Sより左へ行くと、点Qは動かなくなっていくようです。 右下を見ると、点Pが点Tをこえて右へ行けば、点Qは急速に右へ行ってしまうようです。
[2]: こんどは、赤い点Qを等間隔に動かして青い点Pを追従させたものです。 点Pと点Qは、[1]とまったく逆の動き方をしています。 図はとしては、[1]と[2]は合同です。
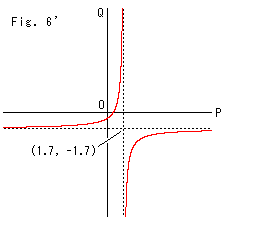
Fig.6'は、P,QをXY座標にとって、Fig.6の点P,Qの相互関係を広い範囲で見てみたものです。 描かれた曲線は、双曲線になっています。
点P,Qがこれらの図のように位置を変えても、複比は変化しないわけです。
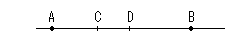 複比の式は見た目に簡単ですが、読み取るにはちょっとややこしいですね。 それで複比をもう一度、定義して復習しておきましよう。 点列A,B,C,Dが右図のように並んでいるときの複比は、線分ABを点Cが分割する比の値
複比の式は見た目に簡単ですが、読み取るにはちょっとややこしいですね。 それで複比をもう一度、定義して復習しておきましよう。 点列A,B,C,Dが右図のように並んでいるときの複比は、線分ABを点Cが分割する比の値 と、同じ線分ABを点Dが分割する比の値
と、同じ線分ABを点Dが分割する比の値 との比の値
との比の値
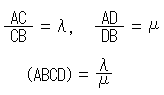 です。
です。
線分はすべて有向線分であって、点Cが図のように内分点なら は正ですが、点Cが外分点になっているときは
は正ですが、点Cが外分点になっているときは は負です。
は負です。
そして、これらの点が虚数(虚点)であっても、そのままで複比だとします。
つぎに、どういったところに複比が当てはまるのか。 そして、射影変換で不変といわれる複比と複比(同じ値の複比どうし)がどのような関係にあるのかを見ていきます。
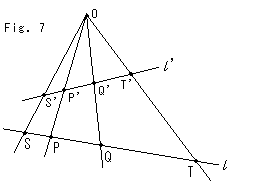 Fig.7は、点Oを射影の中心として、直線
Fig.7は、点Oを射影の中心として、直線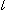 上の4つの点S,P,Q,Tを直線
上の4つの点S,P,Q,Tを直線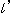 上のS',P',Q',T'に射影したものです。 この射影では
上のS',P',Q',T'に射影したものです。 この射影では
(S'P'Q'T') = (SPQT)
となっています。 4点の組み合わせがどんなであっても、同様です。 射影の中心Oと線分STと線分S'T'の関係は、これまでに見たカメラと地面とスクリーンパネルの関係に相当します。
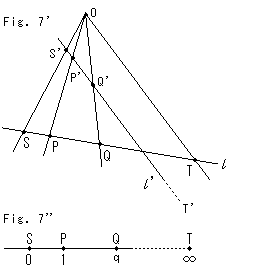 Fig.7'は、直線
Fig.7'は、直線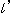 が特別な傾きになっている場合です。 直線OTと直線
が特別な傾きになっている場合です。 直線OTと直線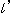 が平行になっていて、両直線の交点をT'として描くことができません。 しかし、交点T'は無限遠に存在すると考えられるので、
が平行になっていて、両直線の交点をT'として描くことができません。 しかし、交点T'は無限遠に存在すると考えられるので、
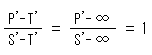
と書けますから、直線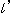 上の複比(S'P'Q'T')は、(SPQT)と等しくて
上の複比(S'P'Q'T')は、(SPQT)と等しくて
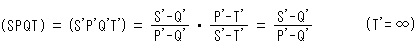 となります。
となります。
同様な考え方をとると、直線上の1つの点qでも複比で
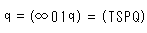
と表わすことができます。 Fig.7''は、このときの点Qの位置です。 点Qは点Tをまたぐことはできません。 いや、あとで分かってきますが、平気でまたげるのです。 無限遠を! 直線が点Tへと延びているところを点線で描いていますが、その必要もないのです。
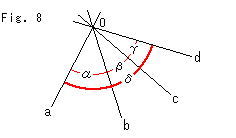 Fig.8をご覧ください。 4本の直線a,b,c,dが1点Oを通っています。 このような直線の束を線束といいます。 直線自体に値はありませんが、線束にも複比をいうことができます。 その一つは、図のように角を表わすと、
Fig.8をご覧ください。 4本の直線a,b,c,dが1点Oを通っています。 このような直線の束を線束といいます。 直線自体に値はありませんが、線束にも複比をいうことができます。 その一つは、図のように角を表わすと、
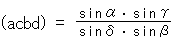
です。 角は、どこからでも左回りを正としておきます。
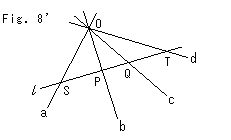 Fig.8'をご覧ください。 線束a,b,c,dを任意の直線
Fig.8'をご覧ください。 線束a,b,c,dを任意の直線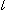 で切っています。 それらの交点をS,P,Q,Tとすると、線束の複比は
で切っています。 それらの交点をS,P,Q,Tとすると、線束の複比は
(acbd) = (SQPT)
と書くことができます。 これを線束の定義だとしても、かまいません。 左辺をアルファベット順にすれば、
(abcd) = (SPQT)
です。
 また、Fig.8''から直ぐに
また、Fig.8''から直ぐに
(abcd) = (SPQT) = (efgh)
であることがいえます。 そして、このことから
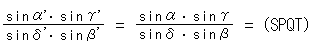
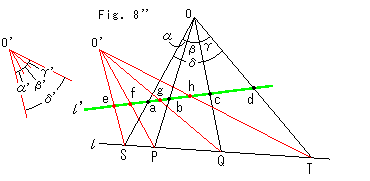
となっていることが分かります。
Fig.9をご覧ください。 4点e,f,g,hと2点U,U'が同じ円周上にあり、黒い線束a,b,c,dと赤い線束a',b',c',d'が描かれています。 しばらく簡単のために、黒い線束をU線束、赤い線束を線束U'と書くことにします。 弦eh上の点列e,f,g,hを点Uと点U'から見た角は同じですから、線束Uの複比と線束U'の複比は等しいことになります。
線束Uを直線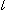 で切ると点列S,P,Q,Tができ、線束U'を直線
で切ると点列S,P,Q,Tができ、線束U'を直線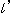 で切ると点列S',P',Q',T'ができます。 これら2つの点列の複比も等しい、つまり、
で切ると点列S',P',Q',T'ができます。 これら2つの点列の複比も等しい、つまり、
(abcd) = (a'b'c'd') = (SPQT) = (S'P'Q'T')
となっています。
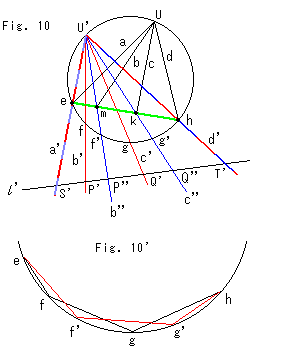 Fig.10をご覧ください。 Fig.9の線束Uを緑色の直線で切って点列e,m,k,hを得ます。 線束Uの弦ehから下は省いています。 点U'から点列e,m,k,hを通る直線を引いて、新しい線束a',b'',c'',d'をつくります。 この新しい線束を青色にしていますが、直線a'と直線d'は線束U'のと重なっているので、赤と青のまだらにしています。 直線
Fig.10をご覧ください。 Fig.9の線束Uを緑色の直線で切って点列e,m,k,hを得ます。 線束Uの弦ehから下は省いています。 点U'から点列e,m,k,hを通る直線を引いて、新しい線束a',b'',c'',d'をつくります。 この新しい線束を青色にしていますが、直線a'と直線d'は線束U'のと重なっているので、赤と青のまだらにしています。 直線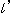 は線束a',b'',c'',d'も切っていて、点列S',P'',Q'',T'をつくっています。
は線束a',b'',c'',d'も切っていて、点列S',P'',Q'',T'をつくっています。
Fig.10'は、Fig.10の線束を省いた円周部分だけを拡大したものです。 円周上の点列も複比をとることができます。 図のように円周上の点列をむすんで弦(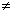 弧)をつくります。 そして、あたかも点列が直線上にあるかのようにとればよいのです。
弧)をつくります。 そして、あたかも点列が直線上にあるかのようにとればよいのです。
このようなことから、
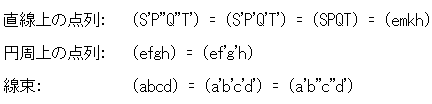
であって、これらすべての複比が等しいことが分かります。
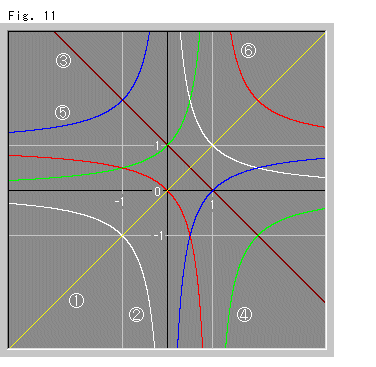
さて、複比はこのようなものですが、Fig.5のどれが長さの定義をするのに使えるのでしようか。
複比 の値を
の値を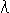 とすると、
とすると、
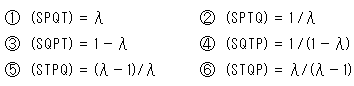
となっています。
Fig.11は、XY座標で、複比 を変化させると、他の複比がどうなるかを見てみたものです。 X軸が
を変化させると、他の複比がどうなるかを見てみたものです。 X軸が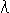 、Y軸が複比です。 灰色の直線は単なる観察用のものです。 これで見ても、どれがよいのか分かりませんね。
、Y軸が複比です。 灰色の直線は単なる観察用のものです。 これで見ても、どれがよいのか分かりませんね。
それぞれの複比にはどんな特徴があるのかを調べてみましよう。
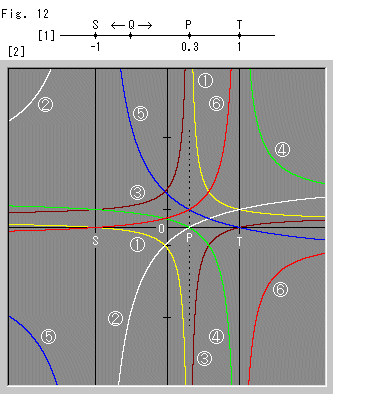
Fig.12をご覧ください。
[1]: 点S,P,Tを固定しておいて、点Qを動かします。 点Pの位置 P = 0.3 は、勝手にとったものです。 点S,Tの位置も点Pを間にはさむように適当にとったものです。
[2]: 点Sや点P,Tのところで、いずれかの複比が発散し符号を換えています。 しかし、点Sと点Tの間(両端を含まない)に限って見ると、青い曲線 と赤い曲線
と赤い曲線 だけは、符号も換えず発散もしていません。 そして、その赤い曲線は、ゼロから無限大へ単調に増加しています。 どうやら、この
だけは、符号も換えず発散もしていません。 そして、その赤い曲線は、ゼロから無限大へ単調に増加しています。 どうやら、この の複比(STQP)が長さの定義に利用できそうですね。 左方向を正にとるなら、
の複比(STQP)が長さの定義に利用できそうですね。 左方向を正にとるなら、 の青い曲線の複比(STPQ)でもよいはずです。
の青い曲線の複比(STPQ)でもよいはずです。
 Fig.13は、Fig.12での
Fig.13は、Fig.12での の複比(STQP)の赤い曲線が、定点Pの位置が変わるとどうなるかを見てみたものです。 曲線の形が、点Pの位置によって違っています。 これでは、複比(STQP)や(STPQ)そのものを距離とすることはできません。
の複比(STQP)の赤い曲線が、定点Pの位置が変わるとどうなるかを見てみたものです。 曲線の形が、点Pの位置によって違っています。 これでは、複比(STQP)や(STPQ)そのものを距離とすることはできません。
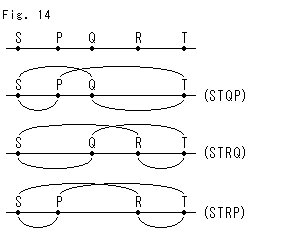 Fig.14をご覧ください。
Fig.14をご覧ください。
直線上に5つの点S,P,Q,R,Tがあります。 そこから のタイプの複比(STQP), (STRQ), (STRP)をつくります。 この3つの複比の関係は、
のタイプの複比(STQP), (STRQ), (STRP)をつくります。 この3つの複比の関係は、
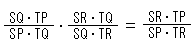
となっています。 カッコの式で書くと、
(STQP)(STRQ) = (STRP) 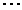 (2)
(2)
です。 これは掛け算ですので、対数をとって足し算に変えます。 区間を限らずに掛け算を足し算に変えることができるのは、対数以外にありません。 対数の底は何でもよいので、自然対数にしておきます。
式(2)の対数をとると、
log(STQP) + log(STRQ) = log(STRP)
となります。 この対数の値を距離の定義(約束)にしようとするわけです。 2点P,Q間の距離をd(PQ)と表わすと、
d(PQ) = k log(STQP) 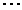 (3)
(3)
と書けます。 このd(PQ)には正負があります。 kは、単位の取り方できめる定数です。 そして、
d(PQ) + d(QR) = d(PR)  (4)
(4)
が成り立つので、距離としてふつうに加減ができます。 ただし、これを計算するには、点S,Tが定まっていなければなりません。 また、距離d(PQ)からふつうの距離PQを逆算するには、点P,Qのいずれかの位置を指定する必要があります。
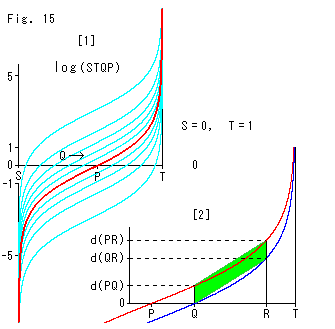
Fig.15をご覧ください。
[1]: 点S,P,Tを固定して、点Qを動かします。 赤い曲線は、点Qが動くときの複比(STQP)の対数の変化です。 定数kは k = 1 にとっています。 水色の曲線は、定点Pの位置を赤い曲線のところから左右に等間隔に変えた場合です。 この水色の曲線は、上下の間隔は一定ではありませんが、どれも同じ形です。
[2]: [1]の右の方を少し拡大しました。 そこに3点P,Q,Rを置いて、上で定義した距離との関係を見たものです。 観察のために添えた緑色の帯は、完全な平行四辺形になっています。 そして、式(4)が成り立っているのが見られます。
曲がったものを曲がった鏡で見れば、真っ直ぐ(線形)に見えるというリクツに似ていますね。
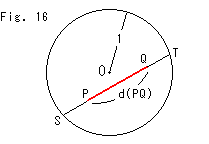 Fig.16は、Fig.3の円に描いたものです。 この円Oの中にある点P,Qを通る弦の両端を点S,Tとして、線分PQの長さを式(3)によってd(PQ)と測ります。 この場合、円Oの半径を1にとってあるので、定数kは 1/2 となり、
Fig.16は、Fig.3の円に描いたものです。 この円Oの中にある点P,Qを通る弦の両端を点S,Tとして、線分PQの長さを式(3)によってd(PQ)と測ります。 この場合、円Oの半径を1にとってあるので、定数kは 1/2 となり、
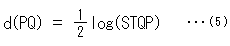
です。 線分PQとその長さd(PQ)の関係はFig.15のようになっていますから、d(PQ)をどんなに大きくとっても、線分PQは円Oからはみ出しません。 ですから、円周を無限遠直線と見立てることができます。
こうした距離を双曲距離(hyperbolic distance)としたものが、クラインの円板モデルです。 それは、計量化した射影平面です。 ここでの計量は、微視的なdsではありません。 大域的で、ときに巨視的です。
この円板は、射影平面をくり抜いて計量化したものといえます。 Fig.15を見ると、計量化は射影平面全体を円形に圧縮することとも察しられそうですね。 でも、そうすると、円板の対心点を同一視しなければならなくなってしまいます。 前に、歪んだ面を平たい円に圧縮しましたが、それは計量化していたことに相当しますね。 でも、あのときは対心点のことなど考えていませんでした。
ともかく、円板モデルの外側はまったく何も無いところです。
円板上では、「ユークリッド平面とのちがいは、あの平行線の公理だけである」といわれています。 それは、点P,Qの間の距離をd(PQ)として測るといった約束のうえでのことです。 そして、その約束での長ささが等しものは合同であるとします。 長さを保った移動のことを等長変換といいますが、その“等長”は、むろん定義にしたがって測った長さです。
以下に作図による等長変換の例をあげておきます。
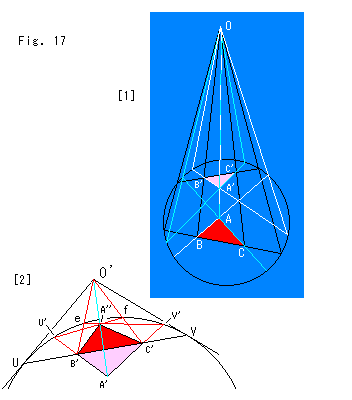
Fig.17をご覧ください。
[1]は、Fig.4と同じ要領で描いたものです。
[2]は、三角形A'B'C'をもう一度裏返す(表側になる)作図です。 その手順は、
1. 頂点B',C'を通る直線を引いて、円との交点U,Vを得る。
2. 点V,Uに円の接線を引き、交点(新しい射影の中心)O'を得る。
3. 辺A'B'と辺A'C'を延長して、円との交点U',V'を得る。
4. 射影の中心O'から頂点B',C'へ直線を引いて、円との交点e,fを得る。
5. 直線eV'と直線fU'の交点A''が、頂点A'に対応する点になる。
です。 直線UVが鏡映の軸になっています。
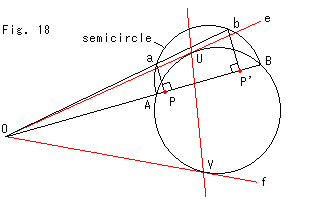
Fig.18は、対応する赤い2点P,P'だけから射影の中心Oを作図で求める方法です。 これは、半球を使わずに、円と同じ平面上の半円(semicircle)で行ったものです。
その手順は、
1. 直線P,P'と円板との交点A,Bを直径とする半円を描く。
2. 点P,P'からす垂線を立て、半円との交点a,bを得る。
3. 直線PP'とabを引けば、その交点が射影の中心Oとなる。
です。
鏡映の軸は、赤い直線のように、射影の中心Oを通る接線Oe,Ofの接点U,Vを通る直線になります。
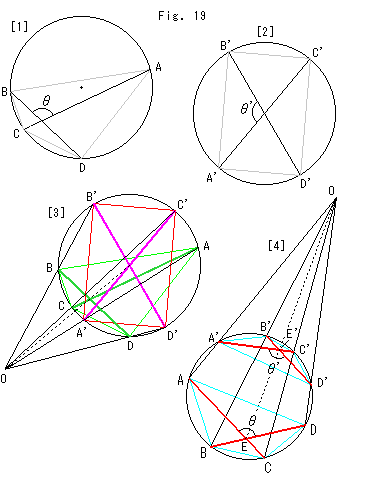 Fig.19をご覧ください。
Fig.19をご覧ください。
[1]: 角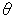 は、クラインの円板内の双曲的角です。 これは、複比で
は、クラインの円板内の双曲的角です。 これは、複比で
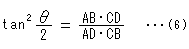
と求められます。 右辺の弦AB,CD,AD,CBは、ユークリッド的長さ(>0)です。
[2]: [1]の対角線の交点を円の中心へ移したものです。 それにつれて、四辺形ABCDが長方形A'D'C'B'になります。 そして、角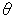 'は
'は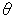 と同じです。 円の中心(原点)では、双曲的な角とユークリッド的な角が一致するので、ふつうの余弦定理と半径が1であることから、
と同じです。 円の中心(原点)では、双曲的な角とユークリッド的な角が一致するので、ふつうの余弦定理と半径が1であることから、
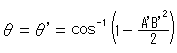 と得られます。
と得られます。
[3]: これは[1]と[2]を重ねて描き、四辺形ABCDをA'D'C'B'へ移す射線を添えたものです。 その射影の中心Oは、円の中心と対角線AC,BDの交点をとって、Fig.18の要領で得ています。
[4]: 対応する四変形の対角線の交角が等しいことを見やすく描いたものです。 [3]も射線との関係はこれと同じです。 円周上の頂点の内角は、すべてゼロになります。
円板の内部が双曲的になっていることは、上で見た通りです。 もちろん、ロバチェフスキーの平行線の公理が利いているとか、曲率が負の一定値あるといったことを調べてもよいのですが、ここでは「巨視的に全体を一望に見て、双曲的である」といっているのです。 微分も積分もつかっていません。
射影幾何には射影幾何としての公理があります。 しかし、ユークリッド平面に無限遠点や無限遠直線をつけ加えれば射影平面が得られるのですから、平行線公理以外の公理は射影幾何でもそのまま通用します。 射影幾何には、もとから平行線はありません。 すべての2直線は、1点で交わることになっています。
射影幾何の公理とユークリッド幾何の公理との違いは、
射影幾何には、距離がなくて無限遠がある。
ユークリッド幾何には、距離があって無限遠がない。
となっています。
そして、
双曲幾何には、(双曲的)距離と無限遠の両方がある
のです。
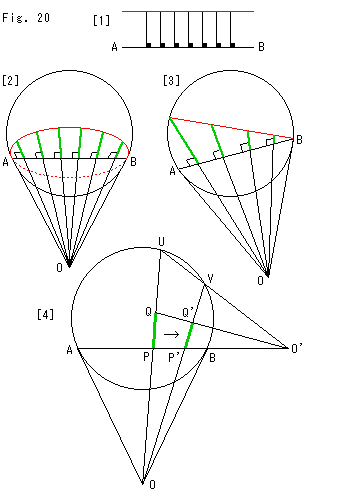 Fig.20をご覧下さい。
Fig.20をご覧下さい。
距離が双曲的になっていることは、等距離線を描くことによっても明らかとなります。
[1]はユークリッド平面上です。 直線AB上に長さの等しい線分を垂直に立てて並べます。  はユークリッド的直角(Euclidean right angle)の印しです。 赤い直線は、その先端をむすんで行ったものです。 直線ABと赤い直線は、いうまでもなくユークリッド平行線になります。
はユークリッド的直角(Euclidean right angle)の印しです。 赤い直線は、その先端をむすんで行ったものです。 直線ABと赤い直線は、いうまでもなくユークリッド平行線になります。
[2]はクラインの円板です。 直線ABの等距離線を描くと、円に内接する赤い楕円になります。 それは、ユークリッド的にも双曲的にも、平行線ではありません。
[3]もクラインの円板です。 赤い直線は、直線ABに双曲的に平行です。 緑色の線分は、直線ABに双曲的に垂直で、平行線の間をむすんでいます。 しかし、線分の長さは、明らかに一定ではありません。
[4]は、[2]の作図法です。 計算によって描くこともできますが、射影でおこないます。 はじめに、点A,Bにおける円の接線の交点Oがあって、その交点Oを通る直線をOU上に、図のように線分PQがあるとします。 線分PQを長さを変えずに右へ移して線分P'Q'とするす手順は、
1. 線分AB上に点Pが移る点P'をとり、直線OP'Vを引く。
2. 直線UVと直線ABとの交点O'を得る。
3. 直線OVと直線O'Qとの交点が点Q'となる。
です。 P'Q'からつぎのP''Q''への移動は、これを繰り返せばよいのです。
ところで、[3]の双曲的平行線とFig.7'とは整合しません。 Fig.7'では距離は定義されていないからです。
[3]の点AやBは無限遠直線とされている円周上にありますが、その無限遠直線は距離の定義を与えたことによって得られたものです。
ということは、ふつうの紙の上に円を描いて、距離や角を複比を用いてFig.16のように測ることさえすれば、その円を円板モデルとしてよいわけです。 それが、これまでにやってきたことです。 射影平面がどうのと意識しなくてすみました。 いま、その内幕が暴かれはじめているのです。
以上でクラインの円板はできたのですが、射影幾何からいろいろな幾何が現れるはずなのに、すんなり双曲幾何だけが出てきましたね。 それは、射影平面にいきなりFig.3の円を描いて出発したからにちがいありません。その円の出所をただしておかないと、スッキリしません。 それに、射影平面には表裏がないということとの関係は、どうなっているのでしようか。
[前章] [次章] [目次]


 射影変換では、点が別の場所に移るだけでなく、角や長さも変わります。 つまり、射影平面の上では、ふつうの計量がありません。 角も距離も合同も関心事ではないのです。 しかし、それでは困ります。 そこで、射影変換に条件をつけて、距離も角も定まるようにします。 そうすることを計量化といいます。
射影変換では、点が別の場所に移るだけでなく、角や長さも変わります。 つまり、射影平面の上では、ふつうの計量がありません。 角も距離も合同も関心事ではないのです。 しかし、それでは困ります。 そこで、射影変換に条件をつけて、距離も角も定まるようにします。 そうすることを計量化といいます。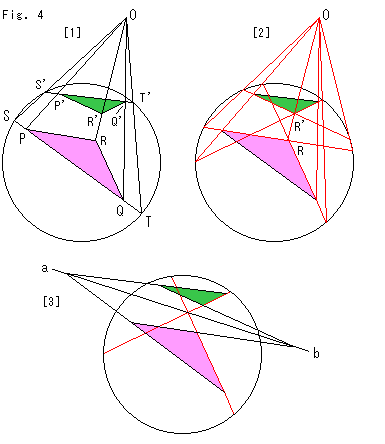 Fig.4をご覧ください。
Fig.4をご覧ください。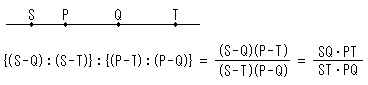

 上のFig.5は、値を異にする複比のリストです。 各複比は、同じ値の4つの複比を1つで代表しています。 それぞれの組み合わせ図の上側は分子で、下側は分母です。 左の列の
上のFig.5は、値を異にする複比のリストです。 各複比は、同じ値の4つの複比を1つで代表しています。 それぞれの組み合わせ図の上側は分子で、下側は分母です。 左の列の
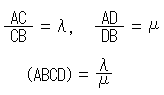
 Fig.7は、点Oを射影の中心として、直線
Fig.7は、点Oを射影の中心として、直線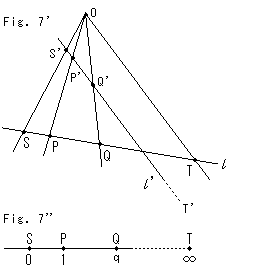 Fig.7'は、直線
Fig.7'は、直線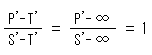
 Fig.8をご覧ください。 4本の直線a,b,c,dが1点Oを通っています。 このような直線の束を線束といいます。 直線自体に値はありませんが、線束にも複比をいうことができます。 その一つは、図のように角を表わすと、
Fig.8をご覧ください。 4本の直線a,b,c,dが1点Oを通っています。 このような直線の束を線束といいます。 直線自体に値はありませんが、線束にも複比をいうことができます。 その一つは、図のように角を表わすと、 Fig.8'をご覧ください。 線束a,b,c,dを任意の直線
Fig.8'をご覧ください。 線束a,b,c,dを任意の直線 また、Fig.8''から直ぐに
また、Fig.8''から直ぐに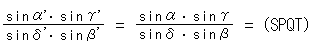

 Fig.10をご覧ください。 Fig.9の線束Uを緑色の直線で切って点列e,m,k,hを得ます。 線束Uの弦ehから下は省いています。 点U'から点列e,m,k,hを通る直線を引いて、新しい線束a',b'',c'',d'をつくります。 この新しい線束を青色にしていますが、直線a'と直線d'は線束U'のと重なっているので、赤と青のまだらにしています。 直線
Fig.10をご覧ください。 Fig.9の線束Uを緑色の直線で切って点列e,m,k,hを得ます。 線束Uの弦ehから下は省いています。 点U'から点列e,m,k,hを通る直線を引いて、新しい線束a',b'',c'',d'をつくります。 この新しい線束を青色にしていますが、直線a'と直線d'は線束U'のと重なっているので、赤と青のまだらにしています。 直線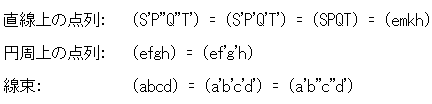

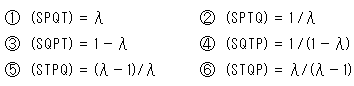

 Fig.13は、Fig.12での
Fig.13は、Fig.12での Fig.14をご覧ください。
Fig.14をご覧ください。
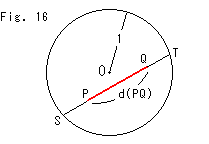 Fig.16は、Fig.3の円に描いたものです。 この円Oの中にある点P,Qを通る弦の両端を点S,Tとして、線分PQの長さを式(3)によってd(PQ)と測ります。 この場合、円Oの半径を1にとってあるので、定数kは 1/2 となり、
Fig.16は、Fig.3の円に描いたものです。 この円Oの中にある点P,Qを通る弦の両端を点S,Tとして、線分PQの長さを式(3)によってd(PQ)と測ります。 この場合、円Oの半径を1にとってあるので、定数kは 1/2 となり、

 Fig.19をご覧ください。
Fig.19をご覧ください。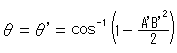
 Fig.20をご覧下さい。
Fig.20をご覧下さい。