第3部 射影幾何から双曲幾何へ
Ch.46 射影幾何 (4) 
無限大 を扱うのにとても有効なテクニックがあります。 それは、同次座標というものです。 それをつかうと、直線や2次曲線などを表わす式が、同次式(各項が同じ次数の式)になります。
を扱うのにとても有効なテクニックがあります。 それは、同次座標というものです。 それをつかうと、直線や2次曲線などを表わす式が、同次式(各項が同じ次数の式)になります。
ここでは同次座標をつかって、実球(実数半径の球)と虚球(虚数半径の球)からクラインの円板をつくります。 そして、見えない虚球を見れるようにした話にたどり着きます。
同次座標は、2つの文字x,yのかわりに3つの文字  ,
,  ,
,  (クシイ,イータ,ツェター)で表わされます。 文字は3つですけれども、あくまで平面上です。 同次座標とふつうの座標(非同次座標)との関係は、
(クシイ,イータ,ツェター)で表わされます。 文字は3つですけれども、あくまで平面上です。 同次座標とふつうの座標(非同次座標)との関係は、
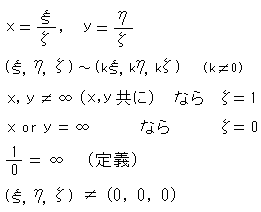 です。 記号"
です。 記号"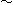 "は同値であることです。
"は同値であることです。
Fig.1の彼には、原点(the origin)から見た2つの点( ,
,  ,
,  )と(k
)と(k , k
, k , k
, k )は同じものに見えています。 同次座標では、原点Oを通る一つの直線上の、原点O以外のすべての点は同じです。 同次座標と非同次座標の交換例をあげると、
)は同じものに見えています。 同次座標では、原点Oを通る一つの直線上の、原点O以外のすべての点は同じです。 同次座標と非同次座標の交換例をあげると、
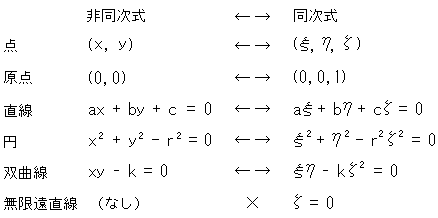
といった具合です。 原点の同次座標は、(0,0,0)ではなくて、(0,0,1)です。 (0,0,0)という点はありません。
同次座標と非同次座標の間は自由に行き来きます。 しかし、前者は無限遠直線を含んでいますが、後者にはそれが無いことを覚えておいてください。 非同次座標から同次座標へ移ったときは、自動的に無限遠直線が付加されるのです。 いいかえると、x,yを ,
, ,
, で表わすと、ふつうの平面から射影平面に変わるのです。 もっとも、x,yのままで射影平面を扱うこともできますが、それは無限遠直線との関わりを除いてのことです。
で表わすと、ふつうの平面から射影平面に変わるのです。 もっとも、x,yのままで射影平面を扱うこともできますが、それは無限遠直線との関わりを除いてのことです。
射影平面をXY座標のように格子線を描いて見れるとよいのですが、それはできせん。
Fig.2は、無理に描いたものです。 斜めの直線  = 0 は、無限遠直線で、座標軸ではありません。 こんな図はまったく観念的で、役に立ちませんね。
= 0 は、無限遠直線で、座標軸ではありません。 こんな図はまったく観念的で、役に立ちませんね。
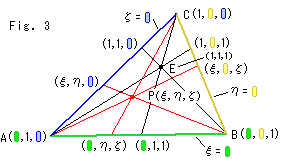
Fig.3は、座標三角形とよばれているものです。 直線  = 0、
= 0、 = 0 と無限遠直線
= 0 と無限遠直線  = 0 から三角形をつくっています。 無限遠直線を他の直線と差別せずに公平に扱っています。 同次座標の点は連比
= 0 から三角形をつくっています。 無限遠直線を他の直線と差別せずに公平に扱っています。 同次座標の点は連比  :
:  :
:  で定まるので、頂点を図のようにとっています。 数字の0や辺に色をつけたのは、見やすくするためです。 点E(1,1,1)は単位点です。
で定まるので、頂点を図のようにとっています。 数字の0や辺に色をつけたのは、見やすくするためです。 点E(1,1,1)は単位点です。
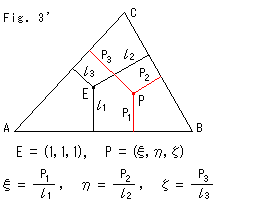 Fig.3'は、点Pの同次座標(
Fig.3'は、点Pの同次座標( ,
,  ,
,  )が三角形ABCの中の単位点E(1,1,1)との位置関係から定まる様子です。
)が三角形ABCの中の単位点E(1,1,1)との位置関係から定まる様子です。  ,
,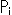 は、三角形ABCの各辺までのふつうの距離です。 単位点Eは、三角形ABCの辺の上でなければ、どこにとってもかまいませんが、それにつれて点Pの座標も変わります。
は、三角形ABCの各辺までのふつうの距離です。 単位点Eは、三角形ABCの辺の上でなければ、どこにとってもかまいませんが、それにつれて点Pの座標も変わります。
点Pが辺BCから三角形ABCの外側に出たときは、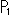 の符号を負にします。
の符号を負にします。 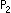 ,
,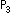 についても同様です。 同次座標で見た場合、辺ACは無限遠直線です。
についても同様です。 同次座標で見た場合、辺ACは無限遠直線です。
この図もFig.3も、これからの話に直接かかわるものではありませんが、見えるものとして添えました。
ところで本来は、射影幾何に座標という考えはありません。 座標をつかうのは、解析的に扱うための便宜的手段です。
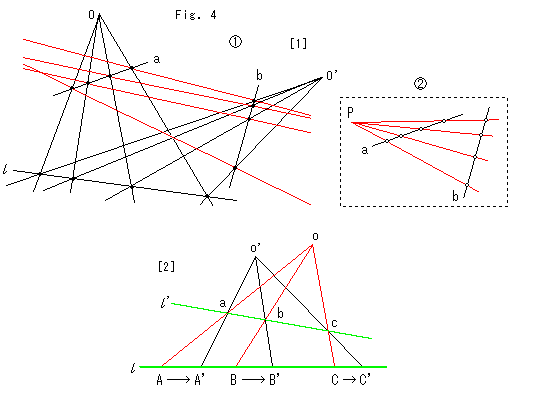 Fig.4をご覧ください。
Fig.4をご覧ください。
射影変換と配景変換の関わりを直線上の点列で見てみます。
[1]:  は線束Oと線束O'が直線
は線束Oと線束O'が直線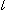 上の4つの点を共有しています。 その4つの点を直線aと直線bに移します。 赤い直線は、直線a上の点とそれに対応する直線b上の点を通したものです。 これで見ると、点線で囲んだ
上の4つの点を共有しています。 その4つの点を直線aと直線bに移します。 赤い直線は、直線a上の点とそれに対応する直線b上の点を通したものです。 これで見ると、点線で囲んだ のように、1つの射影の中心Pをつかって直線a上の4つの点を直線b上に移すことはできません。 対応する点の位置がずれてしうからす。 直線a上の4点を直線b上に移すには、まず直線
のように、1つの射影の中心Pをつかって直線a上の4つの点を直線b上に移すことはできません。 対応する点の位置がずれてしうからす。 直線a上の4点を直線b上に移すには、まず直線 上へ移して、直線
上へ移して、直線 から直線bへと移します。 つまり、配景変換を2回して行うのです。 一般に、任意の直線上の点列を任意の直線上に対応する点列として移すには、配景変換を何度かしなければなりません。
から直線bへと移します。 つまり、配景変換を2回して行うのです。 一般に、任意の直線上の点列を任意の直線上に対応する点列として移すには、配景変換を何度かしなければなりません。
射影変換は、そんな回り道をしないで直接、直線aを直線bに移すものです。 ただし、それは直線という形だけに注目してのことです。 2回の配景変換によったものとは対応点の位置が違います。 適当な射影の中心Pをとって のようにした場合、
のようにした場合、 印の左右の点が対応点になります。
印の左右の点が対応点になります。
[2]: 緑色の直線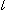 上の点A,B,Cのそれぞれが、赤い線束Oによる配景変換で細い緑色の直線
上の点A,B,Cのそれぞれが、赤い線束Oによる配景変換で細い緑色の直線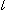 '上の点a,b,cに移り、その点a,b,cは黒い線束O'による配景変換でもとの直線
'上の点a,b,cに移り、その点a,b,cは黒い線束O'による配景変換でもとの直線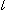 上の点A',B',C'に移っています。 これを射影変換ですると、直線
上の点A',B',C'に移っています。 これを射影変換ですると、直線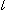 上で→のように直接AからA'へ、BからB'へ、CからC'へと移ります。
上で→のように直接AからA'へ、BからB'へ、CからC'へと移ります。
**************************************************
さて、クラインの円板モデルの円が生まれるところを見ていきます。
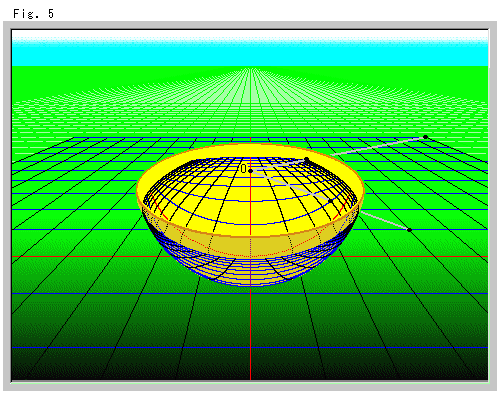
上のFig.5をご覧下さい。 地面(平面)に描かれた格子を半球面に射影しています。 半球面は地面に置かれていて、その中心Oが射影の中心です。 灰色の直線は射線の例です。
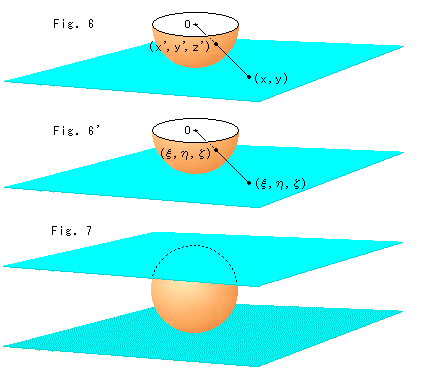
Fig.6は、Fig.5の半球面に座標を書き込んだものです。 半球面の半径は1にとっています。
水色の平面上の点(x, y)の座標を同次座標で表わすことにします。
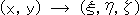 この
この ,
, ,
, は、
は、
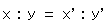
ですから、半球面上の座標(x', y', z')をそのままつかって、
 = x',
= x',  = y',
= y',  = z'
= z'
とすればよいのです。 こうしたのが、Fig.6'です。 平面上の( ,
, ,
, )は同次座標ですが、半球面上の(
)は同次座標ですが、半球面上の( ,
, ,
, )は非同次座標です。 しかし、半球面を変形された平面だとみなせば、半球面も平面もともに射影平面として扱うことができます。 Fig.1を見れば、うなずけますね。
)は非同次座標です。 しかし、半球面を変形された平面だとみなせば、半球面も平面もともに射影平面として扱うことができます。 Fig.1を見れば、うなずけますね。
Fig.7のように、半球のままでは  > 0 の範囲がありませんので、半球面を球面にして、上側にも平面を置きます。
> 0 の範囲がありませんので、半球面を球面にして、上側にも平面を置きます。
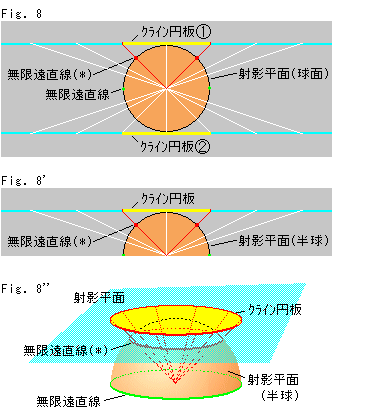
Fig.8は、Fig.7の平面を水平にして、球面の中心を通る垂直な平面で切った断面です。 白い射線は、球面の中心から出ています。 上下どちらの射影平面でもよいのですが、図は上の方をとろうとしています。 射影平面を45 の赤い射線で切ると、球と同じ半径1の円板を作ることができます。 それをクラインの円板にしようとしています。 赤いスポットは、球面上の点で、クライン円板
の赤い射線で切ると、球と同じ半径1の円板を作ることができます。 それをクラインの円板にしようとしています。 赤いスポットは、球面上の点で、クライン円板 の円周に対応しています。 そこにクライン円板
の円周に対応しています。 そこにクライン円板 の立場から見た無限遠直線(*)が通っているとみなします。 みなしたものですので、印し(*)を付けています。 本来の球面上の無限遠直線は球面上の緑色のスポットを通っている赤道です。
の立場から見た無限遠直線(*)が通っているとみなします。 みなしたものですので、印し(*)を付けています。 本来の球面上の無限遠直線は球面上の緑色のスポットを通っている赤道です。
Fig.8'は、Fig.8の下半分を切り捨てたものです。 球全体は必要とはしないことが分かったからです。 これで球面の対心点を同一視することによる問題も同時にケリがつきます。 クライン円板の対心点は同一視されるものではありません。
Fig.8''は、Fig.8'を立体的に見たものです。 平面から赤い縁の黄色い円板をくり抜いて計量化すれば、クラインの円板が得られるというわけです。
それにしても、ちょっとヘンです。 Fig.6'から、平面上でも、つねに
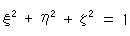
ですから、平面上の点( ,
,  ,
,  )は、この式を満たすものでなければなりません。(この式は同次式ではないので、非同次座標の式に直すことができません。)
)は、この式を満たすものでなければなりません。(この式は同次式ではないので、非同次座標の式に直すことができません。)
この左辺が一定であることから、平面上に
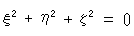
という2次曲線を得ることができます。 これは半径が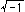 の虚円で、非同次座標で書くと
の虚円で、非同次座標で書くと
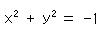
です。 この虚円には、またあとで出会います。 射影幾何では、このような円を絶対円とよんでいます。 ヘンなものが出てきましたね。
それは別として、45 の赤い射線で切るというのは、いかにも作為的な感じがします。 そこで、とりあえず、
の赤い射線で切るというのは、いかにも作為的な感じがします。 そこで、とりあえず、
平面を射影平面とするには、Fig.6'の方法による。
Fig.8''のような構成は、平面から円板を切り取るためだけのものだとする。
ということで、すませておくことにします。
**************************************************
つぎは、虚球の利用です。
虚球をつかうと、くり抜くようなことはしないで、自然な流れで円板が得られます。 虚球に依存すると、本来の幾何が隠されてしまうという意見の人もいます。 たしかに、そうと感じとれるところもあります。 しかし、双曲幾何は虚球面の幾何だともいわれていますので、見捨てるわけにもいきません。
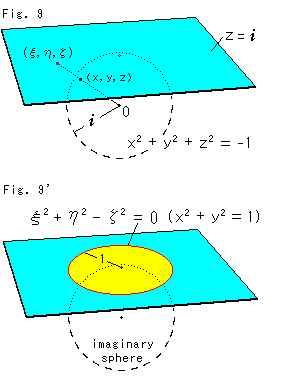 Fig.9をご覧下さい。 丸い点線は、半径
Fig.9をご覧下さい。 丸い点線は、半径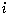 (=
(=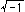 )の虚球です。 空色の平面が虚球の北極に水平に置かれています。 虚球面上の点(x, y, z)を中心Oから空色の平面へ射影した点を (
)の虚球です。 空色の平面が虚球の北極に水平に置かれています。 虚球面上の点(x, y, z)を中心Oから空色の平面へ射影した点を ( ,
,  ,
,  )とします。 すると、こんどは虚球ですから
)とします。 すると、こんどは虚球ですから
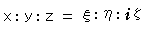
ワァ、虚数の比! ともかく、こうですから、
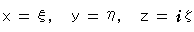
と書けます。 したがって、
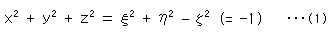
となります。 いうまでもなく、左辺は虚球面上で、右辺は空色の(射影)平面上です。
この左辺は、点(x, y, z)が虚球面上のどこにあっても不変ですから、右辺も平面上で不変です。 そして、その平面上の単位円
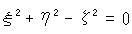
も不変です。 非同次座標で書けば、
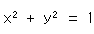
となります。 これも絶対円ですが、これを今度は使います。 右辺が正(実数)ですからxもyも実数となり、実円です。 こうして、Fig.9'のように虚球(imaginary sphere)から自然に実数の単位円が出てきました。 これを計量化すれば、クラインの円板になります。 でも、なにしろ虚球は目に見えないので困ります。
**************************************************
上の式(1)の右側
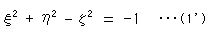 に目をつけて、双曲回転面
に目をつけて、双曲回転面
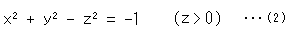
と見比べると、まったく同じ形をしているではありませんか。 これなら、目に見えます。 文字はすべて実数ですから。 そこで、点( ,
,  ,
,  )は平面上の点ですが、それを3次元の点(x,y,z)だとみなして、式(1')を式(2)に書き替えてしまいます。 すると虚球は、双曲回転面に化けて姿を現します。 つまり、
)は平面上の点ですが、それを3次元の点(x,y,z)だとみなして、式(1')を式(2)に書き替えてしまいます。 すると虚球は、双曲回転面に化けて姿を現します。 つまり、
双曲回転面こそ現世における虚球の仮の姿だった
というわけです。
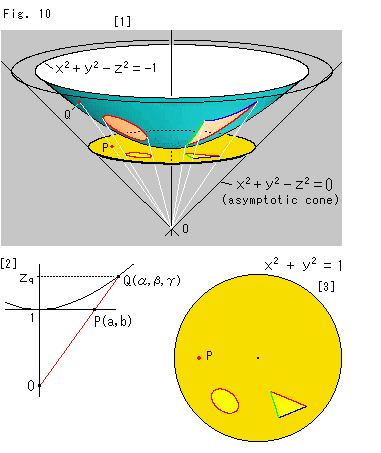 Fig.10をご覧ください。
Fig.10をご覧ください。
[1]: 現れた双曲回転面の漸近錐面(asymptotic cone)の頂点は虚球の中心だったのですから、円板は双曲回転面の底(z = 1)に図のように接したものとなります。 白い射線を見ればわかるように、円板内で点Pがどんなに動いても点Qは双曲回転面から離れることはなく、逆に双曲回転面上で点Qがどんなに動いても点Pは円板の外へ出ることはありません。
[2]: 点Pを(a,b)とし、点Qを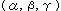 とすると、
とすると、
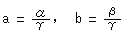
となっています。 つまり、円板上の点の同次座標が、双曲回転面上の対応する点の非同次座標と等しくて、
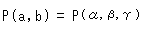 であるわけです。
であるわけです。
双曲回転面上の距離について詮索するのは、省いておきます。
[3]: [1]の円板を真上から見たものです。 だ円は双曲的円です。
虚球を目に見えるものにするもう一つの方法があります。 こんどは式(1)の左側
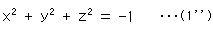
に注目します。 このzを形式的に 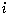 z に書き換えると、双曲回転面の式(2)が得られます。 このあとは上と同様です。
z に書き換えると、双曲回転面の式(2)が得られます。 このあとは上と同様です。
たしかに、巧くいっています。 見事です。 とてもわかり易い。 でも、なにかインチキ臭い気がしませんか。 かってに文字を書き換えるなんて。 いわゆるテクニックだとしておいてよいものでしようか。
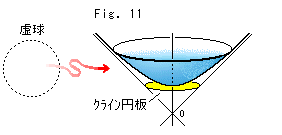
Fig.11のひねった赤い矢印は、マジックのつもりです。 このような手法で、いつも巧くいくとは保証されていません。 可視化したものは、理解のための代用品とでもいえますね。 でも、この双曲面の場合は、100%辻つまが合います。
それにしても、円板をつくることと、その計量化のこととの話のつながりが、いま一つハッキリしていませんね。 群というものがありますが、それを少し覗いてみましよう。 新しい何かがあるかも知れません。
[前章] [次章] [目次]
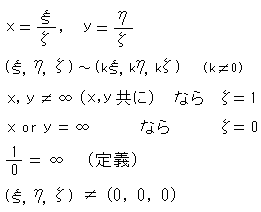

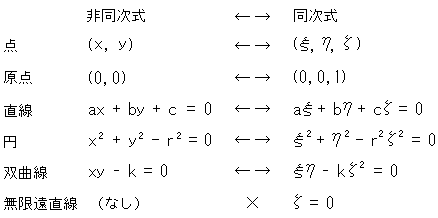

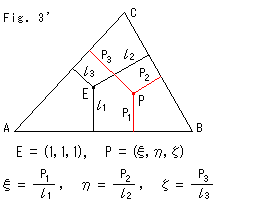 Fig.3'は、点Pの同次座標(
Fig.3'は、点Pの同次座標( Fig.4をご覧ください。
Fig.4をご覧ください。


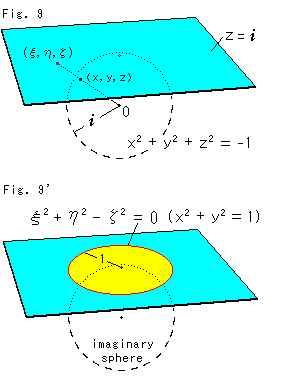 Fig.9をご覧下さい。 丸い点線は、半径
Fig.9をご覧下さい。 丸い点線は、半径 Fig.10をご覧ください。
Fig.10をご覧ください。