第3部 射影幾何から双曲幾何へ
Ch.47 射影変換 と 一次分数変換 
射影変換は、直線を直線に移すものですから線形変換です。 それを同次座標をつかって行列で書くと
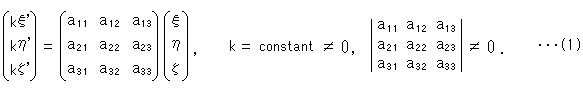
となります。 kはゼロでない定数(constant)です。 この式(1)は、1点( ,
,  ,
,  )の変換を表しています。 他と関係のない1点だけの場合、kは不定です。 しかし、合同などの条件が入ると、kの値が定まります。
)の変換を表しています。 他と関係のない1点だけの場合、kは不定です。 しかし、合同などの条件が入ると、kの値が定まります。
要素 は9個ですが、ゼロでない
は9個ですが、ゼロでない の1つが1になるように全
の1つが1になるように全 を割ってもよいので、実質は8個です。 それにしても、こんな行列は見ただけでは何を物語っているのか、すぐにはわかりませんね。 それに、kは同次座標をつかっていることから意味はわかっても、どう計算されるものなのか見当がつきません。しかし、非同次座標をつかってKを消し去ると、式(1)は
を割ってもよいので、実質は8個です。 それにしても、こんな行列は見ただけでは何を物語っているのか、すぐにはわかりませんね。 それに、kは同次座標をつかっていることから意味はわかっても、どう計算されるものなのか見当がつきません。しかし、非同次座標をつかってKを消し去ると、式(1)は
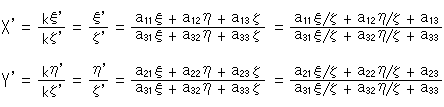 つまり、
つまり、
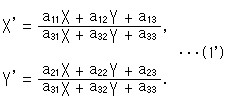 と書けるので簡単です。
と書けるので簡単です。
行列(正則行列)の計算と同じルールが成り立つことを、一言で群をなすとよくいわれます。 実は、ある操作や演算の集合が群であるかないかを判別する一般的な方法はありません。 しかし幸いにも、ここで取り上げる一次分数変換というものも群をなすのです。
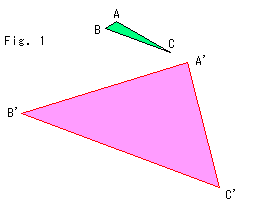 Fig.1をご覧ください。
Fig.1をご覧ください。
ピンクと緑の三角形は大きさも形も違って見えますが、射影変換で動かしたもので、この2つの三角形は合同です。
ふつう、2つの図形が合同というのは、それらがぴったり重ね合わせられることをいいます。 重ね合わせるために図形を動かしても、大きさも形も変化しないとしてのことです。 これはおかしいですね。 大きさも形も変化しないことをどうやって確かめるのですか?
2つの図形が離れていても、合同かどうかを言えるようにしておかねばなりません。 そこで射影変換においては、射影変換で移りあえる図形を合同ということにします。 その前後で図形が見た目にどう変わるかは問いません。 つまり、射影変換で動いた図形は、どこにあっても、どんな格好をしていても、合同だというのです。
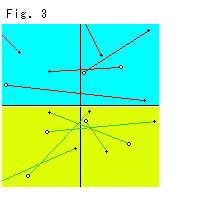
前に虚球面からクラインの円板をつくるのに、
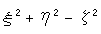
が不変であることを利用しました。 これを射影変換の式(1)で見ると、要素 に
に
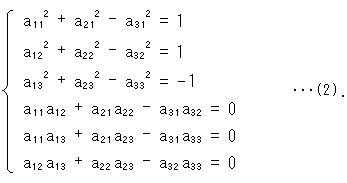
という制限を設けたことになります。 いかにも、窮屈なものに見えますが、このように制限した射影変換も、群をなします。 なぜなら、要素 がどんなものであっても、式(1)が射影変換の式であることに変わりはないからです。 このことは、射影変換に(2)のような条件をつけても、複比が不変であることが保証されているということです。
がどんなものであっても、式(1)が射影変換の式であることに変わりはないからです。 このことは、射影変換に(2)のような条件をつけても、複比が不変であることが保証されているということです。
 Fig.2をご覧ください。
Fig.2をご覧ください。
 : 条件(2)をつけた変換行列(1)の一例です。 計算の便のために、よく
: 条件(2)をつけた変換行列(1)の一例です。 計算の便のために、よく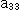 を1にとるのですが、1にすると他の要素が読み取りにくい少数になるので、
を1にとるのですが、1にすると他の要素が読み取りにくい少数になるので、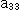 = 3 にしています。 この行列を見ると条件(2)の特徴的なとこころが直ぐに見出せそうですが、実際には数値がさまざまになります。
= 3 にしています。 この行列を見ると条件(2)の特徴的なとこころが直ぐに見出せそうですが、実際には数値がさまざまになります。
 : しかし、その条件つきの行列による射影変換では、クラインの円板の内部の点は内部で、外部の点は外部でしか動けません。 図は、散らばっている点を1個ずつ個別の変換行列で動かしてみたものです。 変換の前後の点を線でむすんでいますが、その線は軌跡ではありません。 たんに関連を描き込んだものです。 赤い線分は、円の内部のあちこちに点をとったもので、動かされた先は内部にとどまっています。 緑色の線分は、円の外部の点をとった場合ですが、その移動先はすべて外側に限られています。 円周上の点は円周上だけでしか動けません。
: しかし、その条件つきの行列による射影変換では、クラインの円板の内部の点は内部で、外部の点は外部でしか動けません。 図は、散らばっている点を1個ずつ個別の変換行列で動かしてみたものです。 変換の前後の点を線でむすんでいますが、その線は軌跡ではありません。 たんに関連を描き込んだものです。 赤い線分は、円の内部のあちこちに点をとったもので、動かされた先は内部にとどまっています。 緑色の線分は、円の外部の点をとった場合ですが、その移動先はすべて外側に限られています。 円周上の点は円周上だけでしか動けません。
**************************************************
上のことは後でまた取り上げることにして、一次分数変換というもの
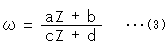
を先に見ていきます。 というのは、射影変換の行列には9個も要素があるために扱いにくいからです。 一次分数変換の文字は一般に複素数です。 しかし、上半平面 に用いられるa,b,c,dは実数であって、そのうえに条件
に用いられるa,b,c,dは実数であって、そのうえに条件
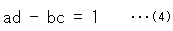
がつけられています。 ですから、上半平面 での一次分数変換の要素はたったの4個で、条件(4)を利用すれば更に少なくなります。 これなら楽に思えますね。
での一次分数変換の要素はたったの4個で、条件(4)を利用すれば更に少なくなります。 これなら楽に思えますね。
この変換は点の動かし方をきめただけのもので、ふつうの平面を上半平面 に変えるものではありません。 上半平面
に変えるものではありません。 上半平面 にするには、長さの測り方(計量)を定める必要があります。
にするには、長さの測り方(計量)を定める必要があります。
一次分数変換も群をなします。 それは、
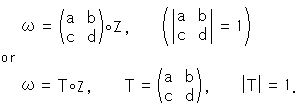
のように一次変換を行列で表現できるからです。 記号"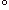 "は式(3)と同じことを表しているのですが、一次分数変換をつづけてn回するときは、この行列Tをn乗すればよいので便利です。
"は式(3)と同じことを表しているのですが、一次分数変換をつづけてn回するときは、この行列Tをn乗すればよいので便利です。
行列のa,b,c,dは変換前後の3点(計6点)できまります。 a,b,c,dを実数に限っても、同様です。
これまで、上半平面 での点の動きがこのような変換によって関係づけられていることに注意を向けませんでした。 そんなものを知らなくても、双曲的直線が半円であり、長さはこう測るのだとわかっていれば、ことが足りました。 しかしいま、その正体にふれ触れようとするのです。
での点の動きがこのような変換によって関係づけられていることに注意を向けませんでした。 そんなものを知らなくても、双曲的直線が半円であり、長さはこう測るのだとわかっていれば、ことが足りました。 しかしいま、その正体にふれ触れようとするのです。
 a,b,c,dが実数である式(3),(4)によって、点はどのように動かされるのでしようか。
a,b,c,dが実数である式(3),(4)によって、点はどのように動かされるのでしようか。
Fig.3をご覧ください。
ふつうの平面上で、さまざまな点を条件(4)のついたさまざまな一次分数変換(3)によって動かします。 X軸(Y = 0)より上の点はX軸より上側だけで、X軸より下の点はX軸より下側だけでしか動きません。 X軸上の点は、X軸上だけで動き、X軸から逸れることはありません。 どの点もX軸をまたぐことは、けっしてありません。 これはまさにFig.2に対応する動きではありませんか!
よく「上半平面をそれ自身に移す」と表現されるのは、上半平面上の点が上半平面上でしか動けないことを指しているのです。
射影変換の式(1)でも、条件(2)を
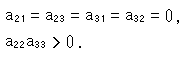 に代えれば、このFig.3と同様な動きになります。
に代えれば、このFig.3と同様な動きになります。
逆に、一次分数変換でFig.2のようにするには、a,b,c,dが複素数になり条件も(4)とはちがいますが、
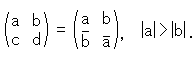 にとればよいのです。
にとればよいのです。
しかし、いずれの場合もa,b,c,dと の対応関係を捉えることは困難です。
の対応関係を捉えることは困難です。
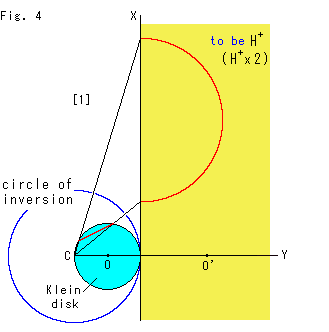 Fig.4をご覧ください。
Fig.4をご覧ください。
上半平面 をクライン円板にむすびつけることは簡単です。 前にも上半平面
をクライン円板にむすびつけることは簡単です。 前にも上半平面 と円板モデルの関係を図にしましたが、ここでは反転円(circle of inversion)をつかって描きます。
と円板モデルの関係を図にしましたが、ここでは反転円(circle of inversion)をつかって描きます。
小さい水色の円Oはクライン円板で、その左端は青い反転円の中心Cに置かれています。 反転によってクライン円板が無限に広い黄色の半平面全体に移っています。 この半平面は実際の上半平面 の2倍になっているので、そのことを含めて見てください。 点O'は、円板の中心Oの対応点です。 反転円の中心を通る円は直線になるので、クライン円板Oの円周が、半平面の縦に描いたX軸になっています。 クライン円板上の赤い弦は双曲的直線で、これと黄色い半平面上の赤い半円が対応しています。
の2倍になっているので、そのことを含めて見てください。 点O'は、円板の中心Oの対応点です。 反転円の中心を通る円は直線になるので、クライン円板Oの円周が、半平面の縦に描いたX軸になっています。 クライン円板上の赤い弦は双曲的直線で、これと黄色い半平面上の赤い半円が対応しています。
さて、クラインの円板がこのように上半平面 になるのですから、それに応じて条件(2)付きの射影変換(1)は、条件(4)付きの一次分数変換(3)に変わるはずです。
になるのですから、それに応じて条件(2)付きの射影変換(1)は、条件(4)付きの一次分数変換(3)に変わるはずです。
つまり、
9個の文字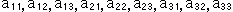 と 6つの条件(2)
の代わりに
と 6つの条件(2)
の代わりに
4個の文字a,b,c,d と 1つの条件(4)
を見ればよいわけです。
これまでに上半平面 で見てきたことは、条件付の射影変換が行われていたことだったのです。
で見てきたことは、条件付の射影変換が行われていたことだったのです。
それはよいのですが、 とa,b,c,dの関係を式で表そうとすると、とてもややこしくなってしまいます。 この図は、その関係式が得られたとして、それによるとこうなるというものです。
とa,b,c,dの関係を式で表そうとすると、とてもややこしくなってしまいます。 この図は、その関係式が得られたとして、それによるとこうなるというものです。
また、図は上半平面 とクライン円板におけるものとして描いていますが、それらには双曲幾何の計量が入っているだけで、ふつうの円とふつうの平面であっても図としては変わりありません。
とクライン円板におけるものとして描いていますが、それらには双曲幾何の計量が入っているだけで、ふつうの円とふつうの平面であっても図としては変わりありません。
一次分数変換でなら、条件(4)を含めた式をつくるのは簡単です。
まず、
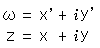 として、実数a,b,c,dの一次分数変換を実部と虚部に分けると、
として、実数a,b,c,dの一次分数変換を実部と虚部に分けると、
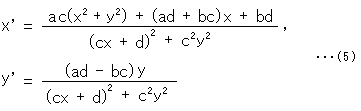
です。 これに条件 ad - bc = 1 を入れると、yとy'はつねに同符号になります。 つまり、Fig.3のようになるわけです。(x'とy'の右辺は、a,b,c,dが複素数ならバランスのよい形になります。)
以下、a,b,c,dは実数で、ad - bc = 1 とします。
aがゼロでないのなら、a = 1 にとれば、d = 1 + bc と書けるので
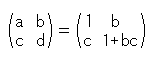 であって、
であって、
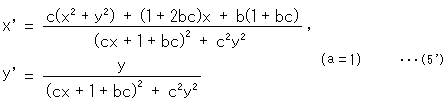
となります。 これで、b,cにどんな値をいれても条件(4)は満たされます。
a = 1, c = 0 にとると、 x' = x + b, y' = y となり、 は横にずれるだけです。
は横にずれるだけです。
aがゼロでもよいのなら、
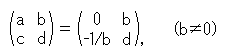 であって、
であって、
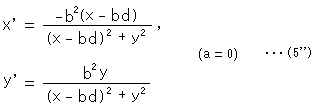
となります。 b(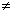 0),d はどんな値でもかまいません。
0),d はどんな値でもかまいません。
この式(5'')は、よく見るとxとx'の符号が逆になる他は、反転の式と同じです。 その反転円は、中心(bd, 0)で半径|b|です。
条件(4)のついた一次分数変換のはたらきを見てみます。
それには2つの方法
abcd固定法: 選んだa,b,c,dを固定しておいてZを変化させる
と
Z固定法: Zを固定しておいてa,b,c,dを変化させる
があります。
いずれによっても、 が動かされます。(方法のよび名は便宜的につけたものです。)
が動かされます。(方法のよび名は便宜的につけたものです。)
一次分数変換を用いる平面の縦軸は、ことわるまでもなく虚軸です。 以下でふつうの平面というのは縦軸が虚軸である平面(ガウス平面)を指しています。
 まずabcd固定法によるのですが、ふつうの平面に条件(4)のついた一次分数変換を適用します。 上半平面
まずabcd固定法によるのですが、ふつうの平面に条件(4)のついた一次分数変換を適用します。 上半平面 がどうのということは、いまは考えません。 ただ見やすいように地色と曲線の色をX軸の上下で変えておきます。
がどうのということは、いまは考えません。 ただ見やすいように地色と曲線の色をX軸の上下で変えておきます。
Fig.5をご覧ください。
直線上の点Zを動かしています。
 : a,b,c,dのどれもゼロでないときです。 直線Zが円
: a,b,c,dのどれもゼロでないときです。 直線Zが円 になっています。 点線は対応する点をむすんだ例です。 この点線は、けっしてX軸(実軸)を横切ることはありません。 矢印は、直線Z上の点がX軸から出発したときの対応する点が動く方向です。 円
になっています。 点線は対応する点をむすんだ例です。 この点線は、けっしてX軸(実軸)を横切ることはありません。 矢印は、直線Z上の点がX軸から出発したときの対応する点が動く方向です。 円 上の点がふたたびX軸にくるのは、直線Z上の点が上下の無限の彼方へ行ってしまったときです。
上の点がふたたびX軸にくるのは、直線Z上の点が上下の無限の彼方へ行ってしまったときです。
 : a,b,c,dのうちのcだけをゼロとしたものです。 直線Zが直線
: a,b,c,dのうちのcだけをゼロとしたものです。 直線Zが直線 になっています。Zと
になっています。Zと は、つねに平行で、同じ方向に延びていきます。
は、つねに平行で、同じ方向に延びていきます。
 : a,b,c,dは
: a,b,c,dは と同様です。 実は、a,b,c,dがそうである場合、Zがどんな図形でも、
と同様です。 実は、a,b,c,dがそうである場合、Zがどんな図形でも、 とZは相似です。 もちろん双曲幾何には相似はありませんが、この平面はふつうの平面です。 Zの図案に意味はありません。
とZは相似です。 もちろん双曲幾何には相似はありませんが、この平面はふつうの平面です。 Zの図案に意味はありません。
c = 0 のときは、Zが直線なら も直線、Zが円なら
も直線、Zが円なら も円です。
も円です。
 : aだけをゼロとしたものです。 この場合も
: aだけをゼロとしたものです。 この場合も と同様に、直線Zが円
と同様に、直線Zが円 になっています。 ただし、円
になっています。 ただし、円 は、必ず原点を通ります。 そのとき直線上の点Zは上下の無限の彼方へと向かっています。 矢印は
は、必ず原点を通ります。 そのとき直線上の点Zは上下の無限の彼方へと向かっています。 矢印は と同様です。
と同様です。
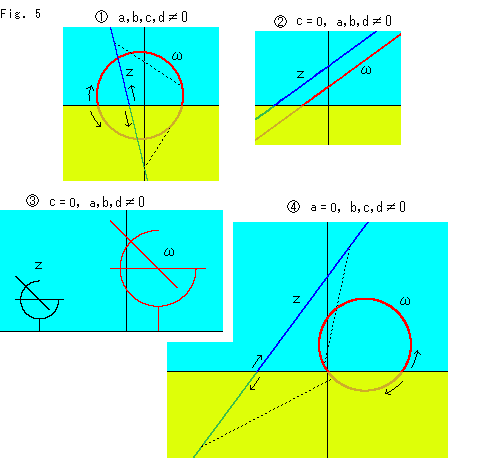
 Fig.6をご覧ください。
Fig.6をご覧ください。
円周上の点Zを動かしています。 a,b,c,dのどれもゼロではありません。
 : この図は3つの行列を
: この図は3つの行列を
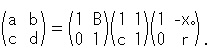
と連ねて作ったa,b,c,dで描いたものです。 もちろん、 ad - bc = 1 を保つようにa,b,c,dに所要の定数をかけて仕上げます。 Bは適当な固定値です。 Xoとrは、円Zの中心のX座標と半径です。 cの値を1つきめて、Zが描く黒い円を変換すると赤い曲線 の1本ができます。
の1本ができます。  が垂線になっているのは c = -1 のときです。 それ以外は
が垂線になっているのは c = -1 のときです。 それ以外は は、 c < -1 では垂線から左側の円になり、 c > -1 では垂線から右側の円になります。
は、 c < -1 では垂線から左側の円になり、 c > -1 では垂線から右側の円になります。
こころみに ad - bc = 0 となるようにしてみると(もはや一次分数変換とはいえませんが)、 はcがどんな値であっても原点とX軸上の赤いスポットのところの2点になって動きません。 赤いスポットは円Zの黒い中心が変換された点
はcがどんな値であっても原点とX軸上の赤いスポットのところの2点になって動きません。 赤いスポットは円Zの黒い中心が変換された点 です。
です。
 : 円が円になっています。 点線は対応点をむすんだ一例です。 黒いスポットは円Zの中心で、その変換された先は赤いスポットになっています。 この赤いスポットは、円
: 円が円になっています。 点線は対応点をむすんだ一例です。 黒いスポットは円Zの中心で、その変換された先は赤いスポットになっています。 この赤いスポットは、円 のユークリッド的な中心になっていません。 円は円に移りますが、中心は中心には移らないのです。
のユークリッド的な中心になっていません。 円は円に移りますが、中心は中心には移らないのです。
こころみにX軸から上は上半平面 だとし、円Zを双曲的円だとして、その双曲的中心を描くと、その位置は黒い星印*のところになります。 それを一次分数変換で変換すると、赤い星印*のところに移ります。 円
だとし、円Zを双曲的円だとして、その双曲的中心を描くと、その位置は黒い星印*のところになります。 それを一次分数変換で変換すると、赤い星印*のところに移ります。 円 は、そのままで双曲的円になっています。 円Zが双曲的円であっても、変わりないのです。 一次分数変換で図形を動かすとき、描かれる平面が上半平面
は、そのままで双曲的円になっています。 円Zが双曲的円であっても、変わりないのです。 一次分数変換で図形を動かすとき、描かれる平面が上半平面 であってもなくても、見た目に変わるところはありません。 違いは、上半平面
であってもなくても、見た目に変わるところはありません。 違いは、上半平面 では長さの測り方がふつうの平面とは異なっているだけです。 そのために、先に円を描いてから中心をしるすと
では長さの測り方がふつうの平面とは異なっているだけです。 そのために、先に円を描いてから中心をしるすと と*のようにずれているのです。
と*のようにずれているのです。
 : 円ZがX軸をまたいでいるので、円
: 円ZがX軸をまたいでいるので、円 もX軸をまたいでいます。 黒と赤のスポットは円の中心です。 この場合も
もX軸をまたいでいます。 黒と赤のスポットは円の中心です。 この場合も の中心はユークリッド的な中心にはなっていません。
の中心はユークリッド的な中心にはなっていません。
つぎはZ固定法によります。 連続した曲線を描くために、特別な約束をしておきます。 ふつうはゼロで割ってはいけないのですが、
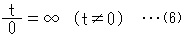
とするのです。 もし同意し難いのなら、極限 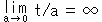 で考えてみてください。 記号
で考えてみてください。 記号 は無限大だとしてもよいし、無限遠点を表すものだとしてもよいことにします。 どちらにしても、正負は考えないか、ご都合次第にします。
は無限大だとしてもよいし、無限遠点を表すものだとしてもよいことにします。 どちらにしても、正負は考えないか、ご都合次第にします。
双曲平面のモデルが閉じたものではない話しと、ここでの約束との関係はどうなるのでしようか。 気にはなりますが、見過ごしてすすむことにします。
固定するZは、ホロサイクルではない円とします。
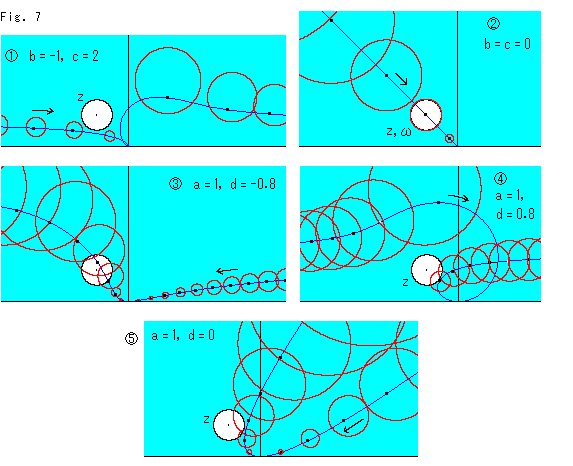 Fig.7をご覧ください。
Fig.7をご覧ください。
ふつうの平面のX軸から上(Y )をつかいます。
)をつかいます。
 : b,cを一定にして、aを変化させ(ゼロでもよい)、dは d = (bc + 1)/a で応動させます。
: b,cを一定にして、aを変化させ(ゼロでもよい)、dは d = (bc + 1)/a で応動させます。
白抜きの黒い円がZで、赤い円が変換された です。 青い曲線は円Zの中心を変換した点の軌跡
です。 青い曲線は円Zの中心を変換した点の軌跡 です。 矢印は、aを負の方から正の方へ変化させていったときに軌跡
です。 矢印は、aを負の方から正の方へ変化させていったときに軌跡 が伸びていく方向です。 a = 0 のとき、軌跡は原点を通ります。 そのとき、d =
が伸びていく方向です。 a = 0 のとき、軌跡は原点を通ります。 そのとき、d =  になり、円
になり、円 は点になります。
は点になります。
円 の大きさが、aの変化につれて変わっていきます。 もしこの平面が上半平面
の大きさが、aの変化につれて変わっていきます。 もしこの平面が上半平面 なっら、同じ大きさとして測られるものです。
なっら、同じ大きさとして測られるものです。
 : b,cをともにゼロにして、
: b,cをともにゼロにして、 と同様にaを変化させたものです。 青い軌跡は半直線になっています。 a < 0 のとき矢印のようにすすみ、a = 0 になると原点に達して折り返します。 そして、a > 0 で、もと来た道をもどります。 途中で円
と同様にaを変化させたものです。 青い軌跡は半直線になっています。 a < 0 のとき矢印のようにすすみ、a = 0 になると原点に達して折り返します。 そして、a > 0 で、もと来た道をもどります。 途中で円 と円Zがぴったりかさなります。 このとき、a = d = 1 になっています。
と円Zがぴったりかさなります。 このとき、a = d = 1 になっています。
 〜
〜 は、a,dを固定してbを動かし、c = (ad -1)/b でcを応動させたものです(b = 0 も可)。
は、a,dを固定してbを動かし、c = (ad -1)/b でcを応動させたものです(b = 0 も可)。
aとbを変化させましたが、cやdを変化させても似た状況になります。 軌跡が左右逆の形になったりするだけです。
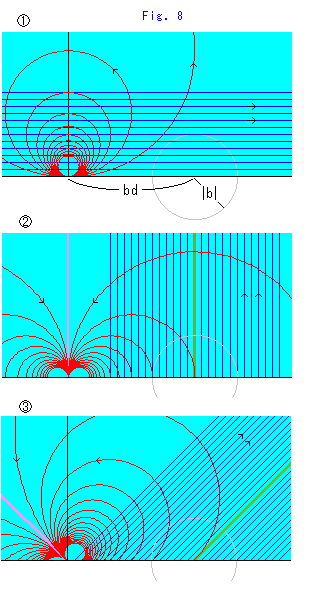
Fig.8をご覧ください。
上と同じ平面をつかって、a,b,c,dを 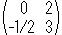 にとって固定します。
にとって固定します。
 : 水平な直線Zを動かします。 赤い円がそれに対応する曲線
: 水平な直線Zを動かします。 赤い円がそれに対応する曲線 で、すべてホロサイクルになっています。 このホロサイクルは、原点できっちり閉じています。 なぜなら、私たちがここで言っている直線Zは左右の無限の彼方まで達しているものと考えているのですから。 灰色の円は、bとbdで定まる反転円です。 矢印は、直線上で点Zを動かしたときの対応する点の動く方向を示しています。
で、すべてホロサイクルになっています。 このホロサイクルは、原点できっちり閉じています。 なぜなら、私たちがここで言っている直線Zは左右の無限の彼方まで達しているものと考えているのですから。 灰色の円は、bとbdで定まる反転円です。 矢印は、直線上で点Zを動かしたときの対応する点の動く方向を示しています。
直線Zが上へ移るにしたがって、円 が小さくなっていきます。 一番上の直線Zと一番小さい円
が小さくなっていきます。 一番上の直線Zと一番小さい円 が対応しています。
が対応しています。
 : 半直線Zを左から右へと動かしています。 赤い
: 半直線Zを左から右へと動かしています。 赤い はすべて半円か垂線になっています。 一番左側の半直線Zと一番小さい右側の赤い半円
はすべて半円か垂線になっています。 一番左側の半直線Zと一番小さい右側の赤い半円 が対応しています。 半直線Zが左から出発して右へといくと、円
が対応しています。 半直線Zが左から出発して右へといくと、円 は急激に大きくなり、半直線Zが反転円の中心を通るところへきたとき、半円
は急激に大きくなり、半直線Zが反転円の中心を通るところへきたとき、半円 は半直線になってしまいます。 そのときの半直線Zを緑色に、
は半直線になってしまいます。 そのときの半直線Zを緑色に、 をピンク色に染めています。 半直線になったピンク色の
をピンク色に染めています。 半直線になったピンク色の はY軸と重なっています。 半直線Zをさらに右へ動かすと、半円
はY軸と重なっています。 半直線Zをさらに右へ動かすと、半円 はY軸の左側に移って、小さくなっていきます。 左側の一番小さい半円
はY軸の左側に移って、小さくなっていきます。 左側の一番小さい半円 と一番右側の直線Zが対応しています。
と一番右側の直線Zが対応しています。
 : 傾けた半直線Zを左上から右下へと動かします。 灰色の反転円の中心を通る緑色の半直線Zとピンク色の半直線
: 傾けた半直線Zを左上から右下へと動かします。 灰色の反転円の中心を通る緑色の半直線Zとピンク色の半直線 が対応しています。 両者の傾きは左右対称です。 それは傾きを変えてもかわりません。 半直線Zが一番左上のとき
が対応しています。 両者の傾きは左右対称です。 それは傾きを変えてもかわりません。 半直線Zが一番左上のとき は、右側の一番小さな欠けた円になっています。 半直線Zが一番右下の隅近くにあるときは、
は、右側の一番小さな欠けた円になっています。 半直線Zが一番右下の隅近くにあるときは、 は、左側の一番小さな欠けた円になっています。
は、左側の一番小さな欠けた円になっています。
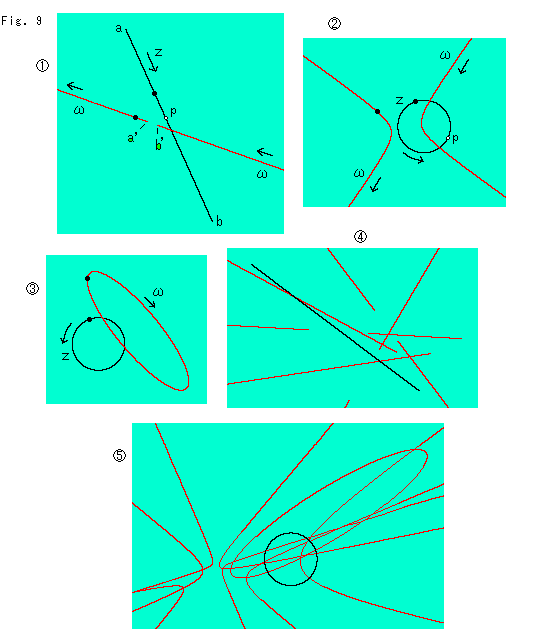 Fig.9をご覧ください。
Fig.9をご覧ください。
射影変換(1)にもどります。 条件(2)をいれないとき、どんな働きをするのかを見てみます。
 : 黒い線分abがZで、赤い線が射影変換された
: 黒い線分abがZで、赤い線が射影変換された です。 黒い線分上で点Zが点aから進むとき、それに対応する点
です。 黒い線分上で点Zが点aから進むとき、それに対応する点 は点a'から進み、左の方の無限遠へ行き、ついで右の方の無限遠から現れて点b'へ戻ってきます。 黒いスポットは対応点の一組の例です。 2点a',b'の間が途切れているのは、黒い線Zが線分だからです。 直線にすれば、赤い線
は点a'から進み、左の方の無限遠へ行き、ついで右の方の無限遠から現れて点b'へ戻ってきます。 黒いスポットは対応点の一組の例です。 2点a',b'の間が途切れているのは、黒い線Zが線分だからです。 直線にすれば、赤い線 は完全につながりまず。 点pは、点
は完全につながりまず。 点pは、点 が無限遠にあるときの対応点Zです。 まさしく射影変換は直線を直線に変換するものです。
が無限遠にあるときの対応点Zです。 まさしく射影変換は直線を直線に変換するものです。
 : 射影変換の行列は
: 射影変換の行列は とまったく同じですが、Zを円にしてみたものです。 一次分数変換では円は円か直線に変換されるのですが、射影変換では円は2次曲線に変換されます。 円が円になるのは特別な場合だけです。 図では
とまったく同じですが、Zを円にしてみたものです。 一次分数変換では円は円か直線に変換されるのですが、射影変換では円は2次曲線に変換されます。 円が円になるのは特別な場合だけです。 図では が双曲線になっています。 白抜き印の点pは、双曲線の無限の彼方にある分枝の先に対応したところです。 分枝は4つですが、その対応点は1点Pです!
が双曲線になっています。 白抜き印の点pは、双曲線の無限の彼方にある分枝の先に対応したところです。 分枝は4つですが、その対応点は1点Pです!
 : 射影変換の行列をちょっと変えたもので、楕円になっています。
: 射影変換の行列をちょっと変えたもので、楕円になっています。
 によっては、むろん曲線
によっては、むろん曲線 が放物線にもなります。
が放物線にもなります。
射影変換が2次曲線を2次曲線に変換するのは、円錐を平面で切った切り口が2次曲線になるのですから、当り前ですね。
変換というものは、原像から写像へとパッと移します。 ゆるやかに連続的に移されていくなら、途中経過がわかって理解しやすいのですが、そうはなっていません。 それで、変換行列をn乗分の1にしたものでn回変換して、途中の様子を見ることを考えます。 ところが、射影変換の行列は3次行列なので、そのn乗分の1を計算するのはとても面倒です。 そこでともかく、適当な射影変換をして、その変換されたものを同じ変換行列でさらに変換し、それをまた変換するといった繰り返しをしてみます。
 : 線分Zの射影変換を繰り返したものです。 当然ですが、直線以外のものにはなりません。 それはよいのですが、途中経過らしきものが現れていないではありませんか。
: 線分Zの射影変換を繰り返したものです。 当然ですが、直線以外のものにはなりません。 それはよいのですが、途中経過らしきものが現れていないではありませんか。
 : 同様に円Zを繰り返し変換したものです。 楕円や双曲線になっています。 2次曲線が退化すると直線になるのですから、直線にもなり得ると思えるのですが、図ではそのような兆しが見えません。 それに、途中経過らしきものも見えません。 どうしてでしようか?
: 同様に円Zを繰り返し変換したものです。 楕円や双曲線になっています。 2次曲線が退化すると直線になるのですから、直線にもなり得ると思えるのですが、図ではそのような兆しが見えません。 それに、途中経過らしきものも見えません。 どうしてでしようか?
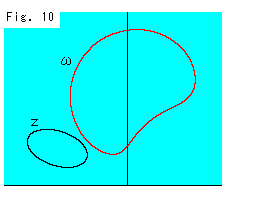
Fig.10をご覧ください。
一次分数変換では、円と直線だけについて見てみてきました。 それは、上半平面 の話しでは、どんな本も円と直線だけを採り上げているのにつられてたからでした。 射影変換では円が2次曲線になるのを見たのですから、一次分数変換でもZを円以外の2次曲線にすると
の話しでは、どんな本も円と直線だけを採り上げているのにつられてたからでした。 射影変換では円が2次曲線になるのを見たのですから、一次分数変換でもZを円以外の2次曲線にすると はどうなるかを見てみます。
はどうなるかを見てみます。
ためしに、abcd固定法で楕円をZにとったのがこの図です。 曲線 は歪んだループになっています。 条件(4) ad - bc = 1 に従っていますが、X軸をまたいで楕円Zを描いても図に変わりはありません。 そして、a,b,c,dをどんなに変えても、
は歪んだループになっています。 条件(4) ad - bc = 1 に従っていますが、X軸をまたいで楕円Zを描いても図に変わりはありません。 そして、a,b,c,dをどんなに変えても、 が直線になることはありません。
が直線になることはありません。
abcd固定法で一次分数変換するZを双曲線とした場合を見てみます。
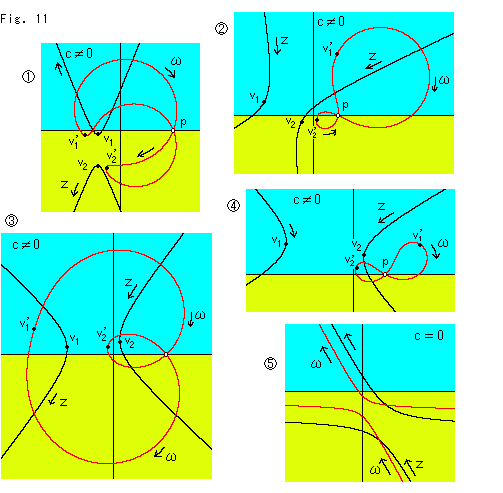
Fig.11をご覧ください。

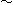
 では、はすべて c
では、はすべて c 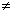 0 にとっています。 赤い曲線
0 にとっています。 赤い曲線 は、歪んだ8の字形か二重巻きのループになっています。 それは、双曲線Zの頂点が2個あるからです。 曲線
は、歪んだ8の字形か二重巻きのループになっています。 それは、双曲線Zの頂点が2個あるからです。 曲線 上の点
上の点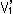 ,
,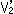 が双曲線Zの頂点
が双曲線Zの頂点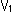 ,
,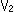 にそれぞれ対応しています。
にそれぞれ対応しています。
X軸上にある白抜き印の点Pは、曲線 がクロスしているところで、Z =
がクロスしているところで、Z = に対応した点
に対応した点 です。 双曲線Zの4つの枝がそれぞれの漸近線に触れようとしながら無限遠へと伸びていますが、その双曲線に対応する
です。 双曲線Zの4つの枝がそれぞれの漸近線に触れようとしながら無限遠へと伸びていますが、その双曲線に対応する は1個の点Pです。 点Pが1個であることはFig.9と同様ですが、曲線
は1個の点Pです。 点Pが1個であることはFig.9と同様ですが、曲線 がそこを2度通過しています。
がそこを2度通過しています。
 は、c = 0 の場合です。 点Pに相当する点はありません。 双曲線Zが無限遠へ伸びていくと、それに連れて曲線
は、c = 0 の場合です。 点Pに相当する点はありません。 双曲線Zが無限遠へ伸びていくと、それに連れて曲線 も無限遠へと伸びていきまいます。
も無限遠へと伸びていきまいます。
いずれの場合も、双曲線ZがX軸を横切るとき曲線 も(点P以外で)X軸を横切っています。
も(点P以外で)X軸を横切っています。
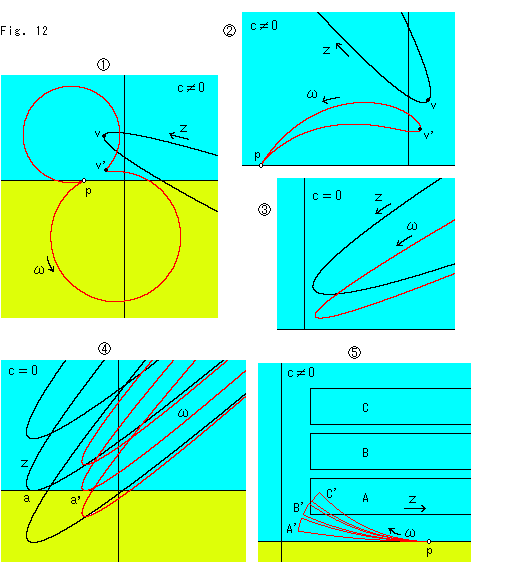
Fig.12をご覧ください。
こんどは放物線Zでの曲線 の様子を見てみます。
の様子を見てみます。  ,
, と
と では c
では c 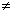 0 で、
0 で、 ,
, では c = 0 です。 a,b,dは、いずれもゼロではありません。
では c = 0 です。 a,b,dは、いずれもゼロではありません。
 : 放物線Zは、図には描かれていませんが、右の方でもX軸を横切っています。 そのため、曲線
: 放物線Zは、図には描かれていませんが、右の方でもX軸を横切っています。 そのため、曲線 も点P以外の2箇所でX軸を横切っています。
も点P以外の2箇所でX軸を横切っています。
視界にある放物線Zの先端はつねに広がっていきますが、その対応点 はここでも1個です。 点vは放物線Zの頂点で、点v'は曲線
はここでも1個です。 点vは放物線Zの頂点で、点v'は曲線 上の対応点です。
上の対応点です。
 : 曲線
: 曲線 が放物線Z上の無限遠に対応する点はここだというように点Pを指しているループになっています。 一次分数変換で無限遠が見える感じがするではありませんか!
が放物線Z上の無限遠に対応する点はここだというように点Pを指しているループになっています。 一次分数変換で無限遠が見える感じがするではありませんか!
 : c = 0 にとっておいて、放物線ZをX軸と交わらないようにすると、Zに相似と平行移動された放物線
: c = 0 にとっておいて、放物線ZをX軸と交わらないようにすると、Zに相似と平行移動された放物線 は上の方にある無限遠直線へと向かいます。 上にも下にも交わらない放物線を描くことはできません。 放物線ZをX軸を横切らない範囲で下の方へ移動すると、放物線
は上の方にある無限遠直線へと向かいます。 上にも下にも交わらない放物線を描くことはできません。 放物線ZをX軸を横切らない範囲で下の方へ移動すると、放物線 だけがX軸を横切りそうに見えますが、そうはなりません。
だけがX軸を横切りそうに見えますが、そうはなりません。
 : そのことを確かめようと放物線Zを下の方へ動かしていったものです。 放物線ZがX軸に接するとき、それと同時に放物線
: そのことを確かめようと放物線Zを下の方へ動かしていったものです。 放物線ZがX軸に接するとき、それと同時に放物線 がX軸に接します。 Zと
がX軸に接します。 Zと のいずれか一方がX軸から離れていることはありません。 そして、放物線ZがX軸を横切ると、放物線
のいずれか一方がX軸から離れていることはありません。 そして、放物線ZがX軸を横切ると、放物線 も放物線ZがX軸を横切ります。
も放物線ZがX軸を横切ります。
 : 曲線ZをX軸に平行なコの字形にすると、右の方へ無限に伸びても上下の無限遠へと向かうことはありません。 すると、曲線
: 曲線ZをX軸に平行なコの字形にすると、右の方へ無限に伸びても上下の無限遠へと向かうことはありません。 すると、曲線 は曲がった楔状のループになります。 コの字曲線上の点Zが右の無限の彼方へ飛び去るとき、点
は曲がった楔状のループになります。 コの字曲線上の点Zが右の無限の彼方へ飛び去るとき、点 が点Pに達します。 点PはX軸上に終始じっとしています。 それもそのはず、点Pの座標は(0, c/a)と計算されるのですから。 でも、なにか神秘的ですね。 コの字形のZを上の方へ A
が点Pに達します。 点PはX軸上に終始じっとしています。 それもそのはず、点Pの座標は(0, c/a)と計算されるのですから。 でも、なにか神秘的ですね。 コの字形のZを上の方へ A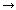 B
B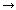 C とずらせていくと、赤い曲がった楔形の曲線
C とずらせていくと、赤い曲がった楔形の曲線 は、 A'
は、 A'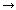 B'
B'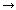 C' と回転します。 これはコの字形のZが、Fig.8の
C' と回転します。 これはコの字形のZが、Fig.8の と
と の部分をとったものと同じだからです。
の部分をとったものと同じだからです。
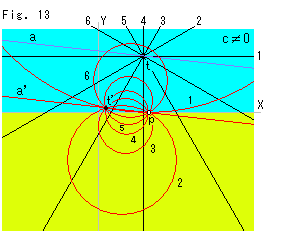
Fig.13をご覧ください。
固定点tを通る直線Zを図のように回転させます。 各直線Zとそれに対応する曲線 に同じ番号をtけています。 Zが直線aのとき、
に同じ番号をtけています。 Zが直線aのとき、 は直線a'になって、2点t',Pを通っています。 点t'は固定点tに対応する点で、点Pは直線Zが無限の彼方へと伸び切ったときの対応点
は直線a'になって、2点t',Pを通っています。 点t'は固定点tに対応する点で、点Pは直線Zが無限の彼方へと伸び切ったときの対応点 です。
です。
Fig.14をご覧ください。
 : 直線Zを一次分数変換し、それを同じ変換行列でまた変換することを繰り返してみたものです。 変換行列をn乗して同じ直線Zを変換しているのです。 赤い曲線
: 直線Zを一次分数変換し、それを同じ変換行列でまた変換することを繰り返してみたものです。 変換行列をn乗して同じ直線Zを変換しているのです。 赤い曲線 につけてある番号と変換行列のnが対応しています。 曲線
につけてある番号と変換行列のnが対応しています。 曲線 の全体を見ると、なめらかな変化のように見えますが、付けられている番号で見ると、ややこしいですね。
の全体を見ると、なめらかな変化のように見えますが、付けられている番号で見ると、ややこしいですね。
 : 円
: 円 のユークリッド中心の軌跡をむすんでいったものです。
のユークリッド中心の軌跡をむすんでいったものです。  が最初に変換された円
が最初に変換された円 の中心です。こうしても様子がよくわかりませんね。
の中心です。こうしても様子がよくわかりませんね。
 : 中心のX座標とY座標を分けて、グラフにしてみました。 X座標の振れ(X-shift)とY座標(Y-shift)の振れの両方がジグザグしています。 これで、いくぶん様子がつかめました。 (n乗された変換行列の移り変わりを取り出してみても、よくわかりません。)
: 中心のX座標とY座標を分けて、グラフにしてみました。 X座標の振れ(X-shift)とY座標(Y-shift)の振れの両方がジグザグしています。 これで、いくぶん様子がつかめました。 (n乗された変換行列の移り変わりを取り出してみても、よくわかりません。)
 : 変換行列を
: 変換行列を と同様に扱ったものです。 こんどはnが増すにつれて円
と同様に扱ったものです。 こんどはnが増すにつれて円 が単調に1点に収斂しています。
が単調に1点に収斂しています。
この と
と の違いは変換行列の固有値によっています。
の違いは変換行列の固有値によっています。  の固有値は複素数ですが、
の固有値は複素数ですが、 の固有値は実数で、しかも重解です。
の固有値は実数で、しかも重解です。
ですから、射影変換でも一次分数変換でも、変換行列をいじくることで滑らかかな途中経過を見ることは、一般的には不可能です。
射影変換へもどります。 その変換行列は、どの3点も同一直線上にない任意の4点とその写像で定まります。 このように点をとることを「4点4点」ということにします。 そのときの は、
は、 を未知数として
を未知数として
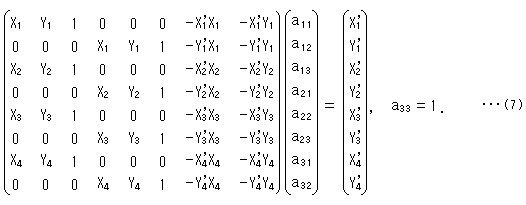
を解けば得られます。 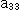 = 1 にしてあるのは、計算の便のためです。
= 1 にしてあるのは、計算の便のためです。
どの3点も同一直線上になという条件をつけているのは、直線上に3点をとると8x8行列が非正則になってしまうからです。 写像の4点はまったく自由にとることができます。 直線上でもかまいません。
射影変換では変換行列がどんなものであっても、直線を直線に移します。 しかし、直線や線分を所要のところへ動かすには式(7)はそのままではつかえません。 不定の解を得て、それに勝手な値を入れてもよいのですが、その値がどんなのであれば、もっともらしいのかの見当がつきません。 そこで、原像の直線をわざと僅かに曲げたもの2本を用いて式(7)から2組の を得ます。 そして、それらの平均値をとって求める
を得ます。 そして、それらの平均値をとって求める だとすることにします。
だとすることにします。
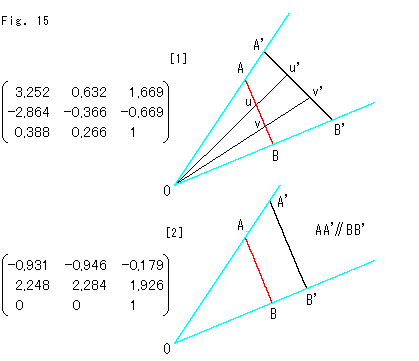 Fig.15をご覧ください。
Fig.15をご覧ください。
[1]: 赤い線分ABを黒い線分A'B'へ移します。 線分AB上の点と線分A'B'上の各点は u u', v
u', v v'のように対応しています。 写像の線がふつうの線分にならずにFig.9の
v'のように対応しています。 写像の線がふつうの線分にならずにFig.9の の
の (そこでは写像が赤い線)のように途切れてはいません。 ちゃんと線分が線分になっています。
(そこでは写像が赤い線)のように途切れてはいません。 ちゃんと線分が線分になっています。
[2]: 写像A'B'が原像ABに平行となるようにしたものです。 変換行列を[1]のとくらべると、1行めと2行めの符号が逆になっており、3行めは0,0,1になっています。
一次分数変換の変換行列は、a,b,c,dを複素数であってもよい場合は、任意の3点とその写像で一通りに定まります。 原像の3点も写像の3点もまったく任意す。 原像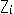 とその写像
とその写像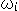 の3組を与えたときの複素数a,b,c,dは、
の3組を与えたときの複素数a,b,c,dは、
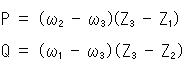 と表して
と表して
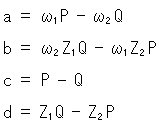 となります。
となります。
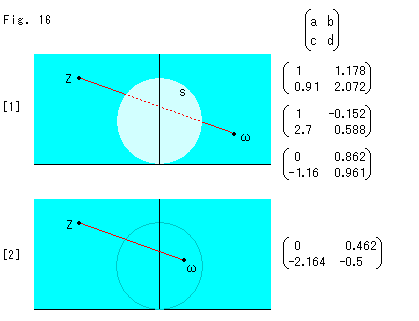 Fig.16をご覧ください。
Fig.16をご覧ください。
a,b,c,dを実数に限ると、上の4つの式a,b,c,dの右辺の虚部がすべてゼロでなければなりません。 そのため、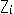 や
や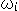 を任意に与えることができなくなります。
を任意に与えることができなくなります。
ところが、a,b,c,d (ad - bc = 1)が実数なら制限はあるけれども、1点Zとその写像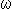 だけでa,b,c,dが定まります。
だけでa,b,c,dが定まります。
[1]: 点Zを与えると、うすく描いてある円Sが定まります。 円Sは、直径がZの実部の大きさYで、中心が虚軸上にあって、原点を通っています。
a = 1 としたとき、この円Sの内部に写像点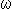 をとることはできません。 そんなことをすれば、a,b,c,dが複素数になってしまいます。 実数として定まるa,b,c,dは、意外にも2通りあります。 計算の途中で、2次方程式が出てくるためです。 また、Zが実軸上のときは
をとることはできません。 そんなことをすれば、a,b,c,dが複素数になってしまいます。 実数として定まるa,b,c,dは、意外にも2通りあります。 計算の途中で、2次方程式が出てくるためです。 また、Zが実軸上のときは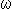 も実軸上に限られ、Y > 0 のときは
も実軸上に限られ、Y > 0 のときは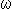 を実軸上にとることはできません。
を実軸上にとることはできません。
a = 0 としても、a = 1 の場合と同じ変換となるa,b,c,dを得ることができます。 つまり、全部で3通りもあるのです。
[2]: a = 0 のときには、円Sの内部に写像点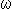 をとることもできます。
をとることもできます。
このように、a,b,c,dが複素数の場合と様子がずいぶん違っています。 a = 1 のとき実数a,b,c,dの組が2つありますが、演算上の理由ではない、もっと本質的なワケを知りたいですね。
**************************************************
さて、思うところへ所要のものを射影変換で動かすことができるようになったので、具体的につかってみます。
 Fig.17をご覧ください。
Fig.17をご覧ください。
まずは変換行列によるのではなく、錘面を切って考えます。
[1]: 円錘面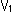 を平面
を平面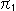 で切ります。 平面
で切ります。 平面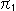 は母線の1つに平行で、その母線と軸をふくむ平面に直交しています。赤い切り口は放物線(parabola)になっています。
は母線の1つに平行で、その母線と軸をふくむ平面に直交しています。赤い切り口は放物線(parabola)になっています。
つぎに、同じ円錘面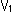 を平面
を平面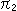 で切ります。 平面
で切ります。 平面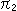 は円錘面
は円錘面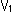 の軸に直交しています。 赤い切り口は円
の軸に直交しています。 赤い切り口は円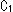 になっています。
になっています。
そして、円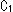 を斜円錘面
を斜円錘面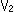 (skew cone)で平面
(skew cone)で平面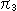 に射影して円
に射影して円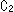 を得ます。 平面
を得ます。 平面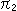 と平面
と平面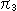 は平行です。
は平行です。
さらに、円錘面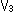 を張ります。 この母線を描くと図が見にくくなるので省いて、円錘面
を張ります。 この母線を描くと図が見にくくなるので省いて、円錘面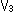 を点線の輪郭線(frame)だけで表現しています。 円錘面
を点線の輪郭線(frame)だけで表現しています。 円錘面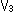 は円
は円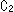 と放物線を含み、平面
と放物線を含み、平面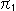 と平面
と平面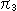 で切られています。
で切られています。
円錘面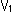 と
と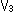 は、いわゆる直円錐の面です。 斜円錘面
は、いわゆる直円錐の面です。 斜円錘面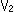 は、直円錐の底面(円)を動かさないで軸を傾けたものです。
は、直円錐の底面(円)を動かさないで軸を傾けたものです。
[2]: 射影的に頂点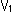 から見ると、平面
から見ると、平面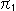 と平面
と平面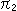 は同一の平面です。 同様に頂点
は同一の平面です。 同様に頂点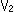 から見ると、平面
から見ると、平面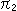 と平面
と平面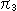 は同一の平面です。 そしてまた、頂点
は同一の平面です。 そしてまた、頂点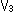 から見れば、平面
から見れば、平面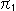 と平面
と平面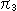 は同一の平面です。 したがって、3つの曲線、円
は同一の平面です。 したがって、3つの曲線、円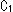 ,
,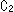 と放物線は同一の平面上にあると考えることができます。 それを描くと
と放物線は同一の平面上にあると考えることができます。 それを描くと のようになっています。 (見やすくするためと作図の都合で、円
のようになっています。 (見やすくするためと作図の都合で、円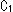 を左の方の放物線の外側へずらせ、円
を左の方の放物線の外側へずらせ、円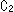 を少し左上にずらせています。)
を少し左上にずらせています。)
円錘面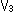 の右の方を確かめるためにスケールを変えて描くと、
の右の方を確かめるためにスケールを変えて描くと、 のようになっています。 円錘面
のようになっています。 円錘面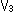 が放物線にちゃんと接しています。
が放物線にちゃんと接しています。
ところで、無限遠では放物線の先端は閉じて無限遠直線に接しています。 放物線の接線の接点を無限の彼方にとったとき、その接線は無限遠直線になるように思われますね。 ところがそうではなくて、驚いたことに、円の中心を通るのだといわれています。 これについては、次章で見てみます。
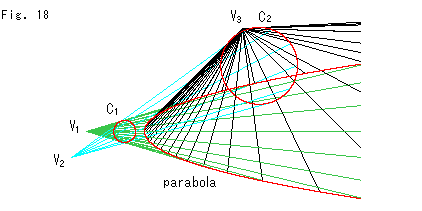 Fig.18をご覧ください。
Fig.18をご覧ください。
上のFig.17の[2]に射線を引いてみました。 立体図のように見えますが、それは円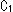 ,
,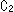 の円周を等間隔にきざんで射線を引いたからです。 図は、あくまで平面上です。
の円周を等間隔にきざんで射線を引いたからです。 図は、あくまで平面上です。
こうしてみると、射影変換における変換の滑らかな経過というのは、錘面を切る平面の一様な動きとみることができます。 また、1つの固定された平面図形を錘面をつかって1つの平面へ射影するときの錘面の一様な動とみることもできます。
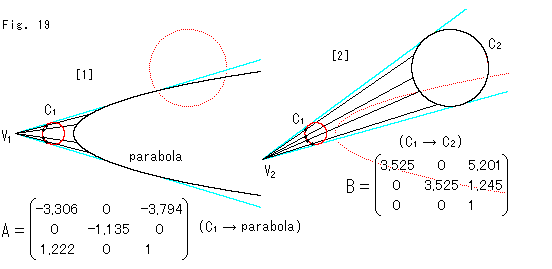 Fig.19をご覧ください。
Fig.19をご覧ください。
上のFig.18の赤い3つの曲線が射影変換としてどうなっているのかを見てみます。
[1]: 円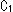 が放物線へ移っています。 その変換行列Aの要素がゼロになっているところに注目してください。 円
が放物線へ移っています。 その変換行列Aの要素がゼロになっているところに注目してください。 円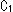 と放物線の軸がX軸上にあります。2次曲線の中心や軸をX軸上にとるときは、いつも
と放物線の軸がX軸上にあります。2次曲線の中心や軸をX軸上にとるときは、いつも 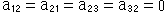 になります。 赤い円
になります。 赤い円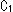 上の4つの黒いスポットは、放物線と対応する射線上の点です。
上の4つの黒いスポットは、放物線と対応する射線上の点です。
[2]: 円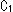 から円
から円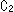 への変換です。 この変換の行列Bでは
への変換です。 この変換の行列Bでは 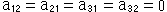 であり、
であり、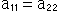 となっています。
となっています。
式(7)に依れば、原像上の4点と写像上の4点を与えれば変換行列が定まります。 図の射線は、その4点4点をとったときのものです。 この場合、[1]では放物線の軸に関して対称に、[2]では2円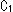 ,
,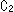 の中心を通る直線に関して対称にしています。 かならずしも対称にとらなくてもよいのですが、そうすることで射影変換としての
の中心を通る直線に関して対称にしています。 かならずしも対称にとらなくてもよいのですが、そうすることで射影変換としての の条件が自動的に満たされています。
の条件が自動的に満たされています。
 にどんな条件を課せばどうなのかといったことには深入りしないで、作図法的にやっていきます。
にどんな条件を課せばどうなのかといったことには深入りしないで、作図法的にやっていきます。
射影変換は二次曲線を二次曲線に移すといわれていることについて見てみます。 その変換行列がどんなものであっても、たしかにそうなります。 しかし、二次曲線は5つの通過点で定まるものです。 4点だけを通る楕円や放物線や双曲線などの二次曲線は無数にあります。 ということは、同じ二次曲線上であっても、どこに4点4点をとるかによって が微妙に変化し、異なる結果となってしまうのです。 とくに、楕円を位置と形を任意に与えた双曲線に移すことは、容易ではありません。 式(7)を真似て10次行列で処理しようとしても、巧くいきません。
が微妙に変化し、異なる結果となってしまうのです。 とくに、楕円を位置と形を任意に与えた双曲線に移すことは、容易ではありません。 式(7)を真似て10次行列で処理しようとしても、巧くいきません。
先に原像と写像の二次曲線を与えておいて4点4点をとる場合でなくても、楕円などをあて推量の変換行列で放物線にすることはとても難しい。 その放物線の位置や形を問わなくても、難しいのです。 それは二次曲線が楕円と双曲線の一方から他方へ変化するときのちょうど境目の一瞬だけに放物線が現れるからです。
そのため、二次曲線を意図する特定の二次曲線に移すには、すこし細工が必要です。 単位円を利用するのです。(愛知教育大の飯島康之先生からのメール指導を参考にしました。)
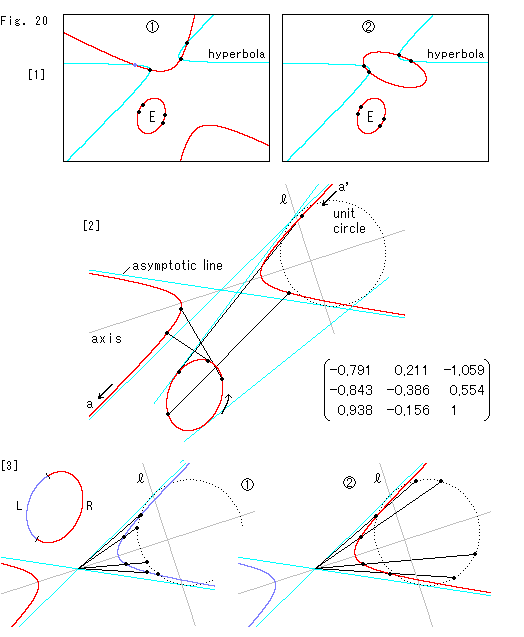
Fig.20をご覧ください。
二次曲線を射影変換で所要の二次曲線に変換することを考えます。
[1]: 楕円Eを水色の双曲線(hyperbola)に移そうとします。 ところが、4点4点をとり変換行列をつくって実行してみると、 では双曲線にはなりますが望むものではありません。
では双曲線にはなりますが望むものではありません。  では楕円になってしまっています。 なぜこんなことになるのでしようか。 それは「射影」変換としての4点4点になっていないからに違いありません。
では楕円になってしまっています。 なぜこんなことになるのでしようか。 それは「射影」変換としての4点4点になっていないからに違いありません。
[2]: 射影変換としての4点4点をとるには、原像と写像がともに錐面に接していることがまず必要です。 双曲線なら漸近線(asymptotic line)と円錐の輪郭線が一致していてることです。 そのために、仲介役の単位円(unit circle)を図のように漸近線にはめます。 左側にはめてもかまいません。 楕円をこの単位円に射影して、その単位円を双曲線に射影します。 つまり、配景変換を2回しているのです。 図の行列は、その2回の変換を掛け算で1つの変換行列にしたものです。 これをつかうことで楕円を一気に所要の双曲線にできます。
黒い線は対応点の例を結んだものです。 直線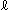 は双曲線の軸(axis)に直交していて、単位円と漸近線の交点を通っています。 この直線
は双曲線の軸(axis)に直交していて、単位円と漸近線の交点を通っています。 この直線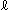 については次のFig.21で取り上げます。 楕円上の点が矢印の向きに動くとき、双曲線上の点はaの方向に去ったあとa'の枝に現れます。 無限の彼方でaとa'は継ながっているのですね。 メビウスの帯と同じです。
については次のFig.21で取り上げます。 楕円上の点が矢印の向きに動くとき、双曲線上の点はaの方向に去ったあとa'の枝に現れます。 無限の彼方でaとa'は継ながっているのですね。 メビウスの帯と同じです。
[3]: 楕円のどこが双曲線の左右の枝にどう対応しているかを見ておきます。  のように直線
のように直線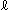 から左側の単位円と双曲線の4点4点をとったときは、対応するところが色分けしたようなっています。 4点4点を
から左側の単位円と双曲線の4点4点をとったときは、対応するところが色分けしたようなっています。 4点4点を のようにとると、双曲線の対応するところが逆になります。 単位円を左側の漸近線にはめたときは、これらと逆になります。
のようにとると、双曲線の対応するところが逆になります。 単位円を左側の漸近線にはめたときは、これらと逆になります。
Fig.21をご覧ください。
Fig.17からFig.19へときた、そのつづきをします。
[1]: 変換行列Bの逆行列 で円
で円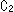 を円
を円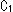 へ移します。
へ移します。
ついで、その円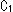 を変換行列Aで放物線に移します。 これで円
を変換行列Aで放物線に移します。 これで円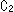 が放物線に移っています。 式でいえば、行列Cで変換しています。 変換行列は1つですが、配景変換2回分の機能をもっているのです。 この変換でのいくつかの点の対応を辿ると、
が放物線に移っています。 式でいえば、行列Cで変換しています。 変換行列は1つですが、配景変換2回分の機能をもっているのです。 この変換でのいくつかの点の対応を辿ると、 のような折れ線になっています。 円
のような折れ線になっています。 円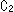 から放物線への対応点の見やすいところをむすんでみると、
から放物線への対応点の見やすいところをむすんでみると、 のようになっています。
のようになっています。
[2]: 円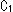 を放物線へ直接移しています。
を放物線へ直接移しています。  が全体の様子で、
が全体の様子で、 は頂点
は頂点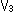 付近を見やすく拡大したものです。 行列Dがその変換行列ですが、行列Cとは一致していません。 行列Cも行列Dも円
付近を見やすく拡大したものです。 行列Dがその変換行列ですが、行列Cとは一致していません。 行列Cも行列Dも円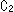 を放物線へ移すものですが、変換行列Dによるときは対応点を通る直線が1点
を放物線へ移すものですが、変換行列Dによるときは対応点を通る直線が1点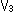 を共有するのにたいして、変換行列Cによるときはそのような共有点はありません。 行列Dによる変換は、配景変換を連ねたものではなくて、頂点
を共有するのにたいして、変換行列Cによるときはそのような共有点はありません。 行列Dによる変換は、配景変換を連ねたものではなくて、頂点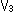 を射影の中心とする射影変換だからです。 同じ形の放物線であっても、[1]と[2]では対応する点の位置関係が大きく異なっています。
を射影の中心とする射影変換だからです。 同じ形の放物線であっても、[1]と[2]では対応する点の位置関係が大きく異なっています。
けれども、配景変換というのは他の射影との関係で見るときの呼称であって、1つの錘面に限れば配景変換は射影変換と同じものです。 放物線と円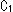 は合同であり、円
は合同であり、円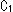 と円
と円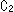 は合同であり、円
は合同であり、円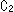 と放物線は合同です。 したがって、円
と放物線は合同です。 したがって、円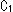 と円
と円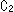 と放物線の三者は合同だというわけです。
と放物線の三者は合同だというわけです。
こうしてきてみると、3つの二次曲線をFig.17の[2]の囲みのようには配置しないで、1つの円錐にはめたもので考えればよいことになります。
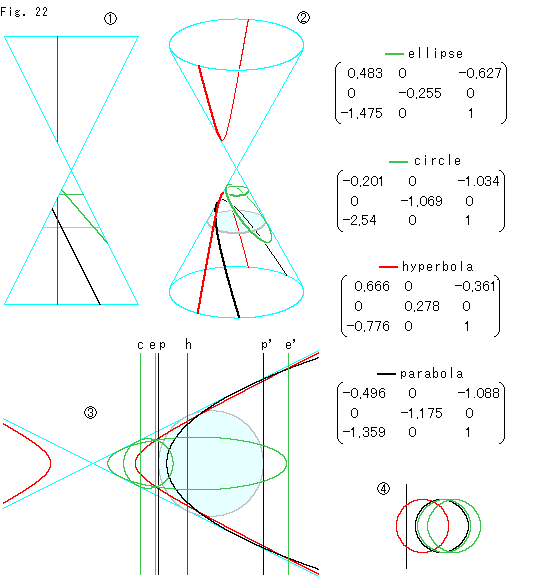 Fig.22をご覧ください。
Fig.22をご覧ください。
 : 円錐をこのように平面で切ると、二次曲線ができます。 切る平面を画面に垂直にそろえたのは作図の便のためだけです。
: 円錐をこのように平面で切ると、二次曲線ができます。 切る平面を画面に垂直にそろえたのは作図の便のためだけです。
 : すこし回して傾けると、立体感が出ます。 うすく水色に塗ってあるのが単位円です。 こい緑色のが円と楕円(ellipse)で、赤いのが双曲線(hyperbola)、黒いのが放物線(parabola)です。
: すこし回して傾けると、立体感が出ます。 うすく水色に塗ってあるのが単位円です。 こい緑色のが円と楕円(ellipse)で、赤いのが双曲線(hyperbola)、黒いのが放物線(parabola)です。
 : それらを円錐の軸を通る1つの平面上に置きます。 二次曲線の軸は円錐の軸と重なっています。 円錐の母線(輪郭線)が双曲線の漸近線になっており、その漸近線に円と楕円と放物線が接しています。 単位円も漸近線に接しています。 原点はX軸上なら、どこにとってもかまいません。
: それらを円錐の軸を通る1つの平面上に置きます。 二次曲線の軸は円錐の軸と重なっています。 円錐の母線(輪郭線)が双曲線の漸近線になっており、その漸近線に円と楕円と放物線が接しています。 単位円も漸近線に接しています。 原点はX軸上なら、どこにとってもかまいません。
行列は、円錐の頂点(漸近線の交点)を射影の中心として、単位円をこれらの二次曲線に移す変換行列です。 どの行列も 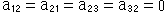 になっています。 X軸を垂直に切っている直線c,e,p,,,は、変換行列の3行目の要素で、
になっています。 X軸を垂直に切っている直線c,e,p,,,は、変換行列の3行目の要素で、
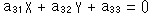
と表されるものです。 これは、非同次座標で書けば
 であって、
であって、 としたものですから、無限遠直線にほかなりません。 直線e,c,h,pはそれぞれ円、楕円に、双曲線、放物線に対するものです。 直線e'も同じ楕円に対するものですが、変換行列は表示のものとは異なります。 直線p'についても同様です。 円にも直線cとは別にもう1つの無限遠直線があるのですが、ずっと左の方にあって画面から外れています。
としたものですから、無限遠直線にほかなりません。 直線e,c,h,pはそれぞれ円、楕円に、双曲線、放物線に対するものです。 直線e'も同じ楕円に対するものですが、変換行列は表示のものとは異なります。 直線p'についても同様です。 円にも直線cとは別にもう1つの無限遠直線があるのですが、ずっと左の方にあって画面から外れています。
そうです。 この単位円は、二次曲線のすべてが円に化けて、無限の彼方で出現しているものです。 図 では見えない右の方や左の方も無限遠ですが、その無限遠がここに住んでいるのですから、スゴイ! いろいろ、想いを巡らせてください。
では見えない右の方や左の方も無限遠ですが、その無限遠がここに住んでいるのですから、スゴイ! いろいろ、想いを巡らせてください。
 : 無限遠直線が何本もあるように描かれているのは何か不自然に感じられますね。 実際の無限遠直線はただ1つであって、単位円が二次曲線に応じて動くのだとする方がよいでしょう。 単位円の色を対応する二次曲線の色に合わせています。
: 無限遠直線が何本もあるように描かれているのは何か不自然に感じられますね。 実際の無限遠直線はただ1つであって、単位円が二次曲線に応じて動くのだとする方がよいでしょう。 単位円の色を対応する二次曲線の色に合わせています。
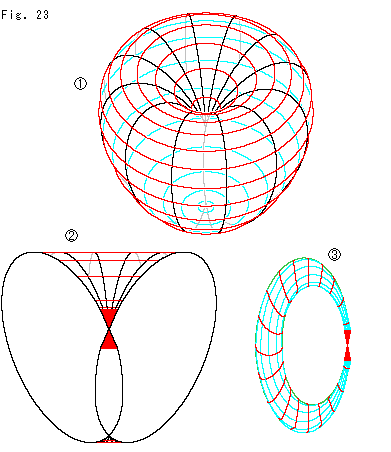
Fig.23をご覧ください。
上の円錐は、実際には上下に無限の彼方へと延びています。 そして、メビウスの帯と同様に180 捩れて継ながています。 図はそれを空想して描いたものです。
捩れて継ながています。 図はそれを空想して描いたものです。  はリンゴのような格好をしている曲面です。 それを真っ直ぐに立てて断面を見ると、
はリンゴのような格好をしている曲面です。 それを真っ直ぐに立てて断面を見ると、 のようになっています。 リンゴの芯のあたりに私たちの円錐曲面があります。 しかし、曲面が自己交差しています。
のようになっています。 リンゴの芯のあたりに私たちの円錐曲面があります。 しかし、曲面が自己交差しています。
自己交差が気に入らないなら、捩れたトーラスで円錐状のくびれたところがあるものを想ってもよいでしよう。  がそれです。 でもこれはバランスのよくない形ですね。
がそれです。 でもこれはバランスのよくない形ですね。
いずれにしても、現実の空間として捉えることはできません。 そうではなく、無限というものの機能を図にして想うまでのことです。
下のFig.24をご覧ください。
原像の単位円だけをX軸上に固定し、写像の二次曲線は1つの円錐の中に閉じ込めることはしないでおきます。 変換行列を図にあるようにとります。 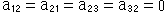 ですので、二次曲線の軸は終始X軸上にあります。
ですので、二次曲線の軸は終始X軸上にあります。  は、単位円から無限遠直線
は、単位円から無限遠直線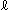 までの距離をX
までの距離をX として
として 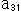 = -1/X
= -1/X にとります。 こうすると、
にとります。 こうすると、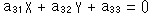 がつねに満たされます。 そして、無限遠直線
がつねに満たされます。 そして、無限遠直線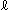 を動かします。 無限遠直線はつねにX軸に垂直です。 そのときの射影の中心は自動的に定まりますが、描画は省きます。
を動かします。 無限遠直線はつねにX軸に垂直です。 そのときの射影の中心は自動的に定まりますが、描画は省きます。
射影変換の変換行列の要素 は9個もあるので、式(7)によらずに、それを定めようとすると、しばしば途方にくれます。 ところがここでは、たったの3個で済むのですから有難い。
は9個もあるので、式(7)によらずに、それを定めようとすると、しばしば途方にくれます。 ところがここでは、たったの3個で済むのですから有難い。 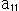 ,
,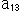 ,
,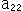 はパソコンの乱数から適当に選んだものです。 ヤマカンで選ぶのもさほど困難はありません。
はパソコンの乱数から適当に選んだものです。 ヤマカンで選ぶのもさほど困難はありません。
順に見ていきましよう。水色に塗ってあるのが単位円です。
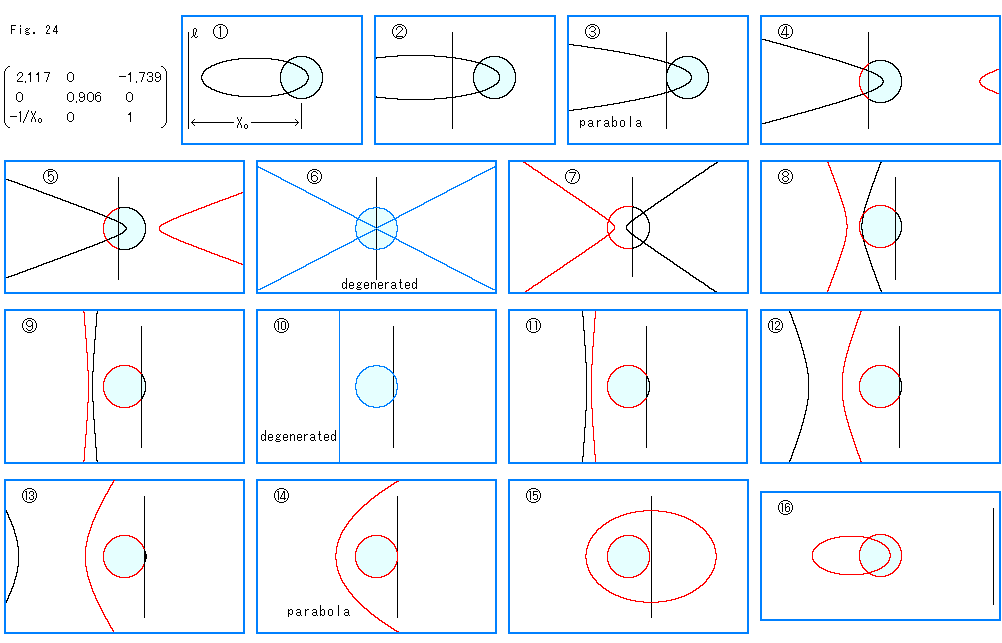
 : ずっと左の方にあった無限遠直線が単位円へ近づいてきたところです。 このあたりから楕円の形の変化が著しくなってきます。
: ずっと左の方にあった無限遠直線が単位円へ近づいてきたところです。 このあたりから楕円の形の変化が著しくなってきます。
 : 楕円の横巾が大きくなってきました。
: 楕円の横巾が大きくなってきました。
 : 無限遠直線が単位円に接して、楕円が放物線(parabola)になった瞬間です。
: 無限遠直線が単位円に接して、楕円が放物線(parabola)になった瞬間です。
 : 無限遠直線が単位円を切りはじめました。 曲線は双曲線になり、その分枝が右の方から現れてきました。 曲線の色分けは対応関係を表しています。
: 無限遠直線が単位円を切りはじめました。 曲線は双曲線になり、その分枝が右の方から現れてきました。 曲線の色分けは対応関係を表しています。
 : 双曲線の二枝がたがいに近づいています。 ただし、黒い枝の方は単位円の中心に達してはいません。
: 双曲線の二枝がたがいに近づいています。 ただし、黒い枝の方は単位円の中心に達してはいません。
 : 双曲線が単位円の中心を交点とする2直線に退化(degenerated)したところです。 このとき、単位円の左右と曲線の対応関係をいうことはできません。
: 双曲線が単位円の中心を交点とする2直線に退化(degenerated)したところです。 このとき、単位円の左右と曲線の対応関係をいうことはできません。
 : ふつうの双曲線にもどっていますが、単位円との対応関係が交換されています。
: ふつうの双曲線にもどっていますが、単位円との対応関係が交換されています。
 : 双曲線の二枝が離れて立ってきます。
: 双曲線の二枝が離れて立ってきます。
 : その二枝が再び接近して、さらに立ってきます。
: その二枝が再び接近して、さらに立ってきます。
 : 双曲線が、こんどは一直線に退化しました。
: 双曲線が、こんどは一直線に退化しました。
 : 再びふつうの双曲線になりました。 単位円との対応関係がまた交換されています。いや、双曲線の枝と枝が無抵抗に透過し合っているようようですね。
: 再びふつうの双曲線になりました。 単位円との対応関係がまた交換されています。いや、双曲線の枝と枝が無抵抗に透過し合っているようようですね。
 : 双曲線の二枝が離れていきます。
: 双曲線の二枝が離れていきます。
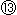 : 双曲線の左の枝だけが大きく離れていきます。
: 双曲線の左の枝だけが大きく離れていきます。
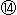 : 無限遠直線が単位円の右側に接して、ふたたび放物線になりました。 単位円との対応関係は
: 無限遠直線が単位円の右側に接して、ふたたび放物線になりました。 単位円との対応関係は とは逆です。
とは逆です。
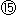 : 楕円になっています。
: 楕円になっています。
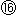 : 楕円は
: 楕円は と同様に、単位円の左寄りになっています。 無限遠直線をさらに右の方へ動かしても、楕円はもうほとんど変化しません。
と同様に、単位円の左寄りになっています。 無限遠直線をさらに右の方へ動かしても、楕円はもうほとんど変化しません。
こうして有限と無限のかかわりを同時に見ることができました。 この例では楕円が円になることはありませんが、変換行列によっては円にもなり、縦に押しつぶされた線分にもなります。
一次分数変換でもこれに相応するものが得られないでしょうか? 一次分数変換はいわゆる円々対応ですから、相似変換以外では円と直線しか対象になりません。 それでも、何か工夫できそうな気がします。 でも、いまそれに手を染めて滞るよりも、先へ行く方がよいでしょう。
[前章] [次章] [目次]
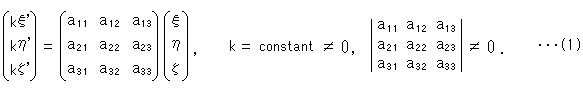
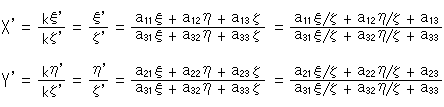
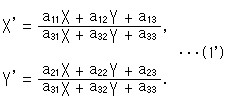
 Fig.1をご覧ください。
Fig.1をご覧ください。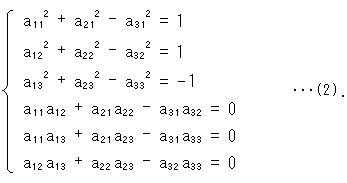
 Fig.2をご覧ください。
Fig.2をご覧ください。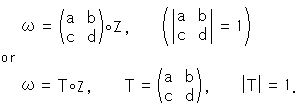
 a,b,c,dが実数である式(3),(4)によって、点はどのように動かされるのでしようか。
a,b,c,dが実数である式(3),(4)によって、点はどのように動かされるのでしようか。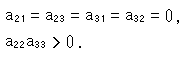
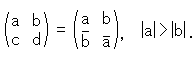
 Fig.4をご覧ください。
Fig.4をご覧ください。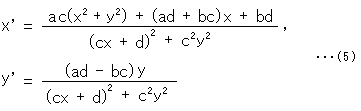
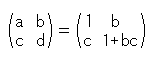
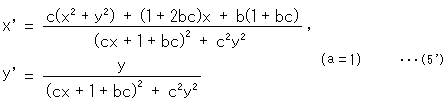
 まずabcd固定法によるのですが、ふつうの平面に条件(4)のついた一次分数変換を適用します。 上半平面
まずabcd固定法によるのですが、ふつうの平面に条件(4)のついた一次分数変換を適用します。 上半平面 Fig.6をご覧ください。
Fig.6をご覧ください。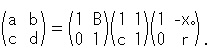
 Fig.7をご覧ください。
Fig.7をご覧ください。
 Fig.9をご覧ください。
Fig.9をご覧ください。




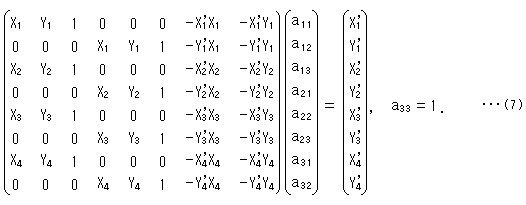
 Fig.15をご覧ください。
Fig.15をご覧ください。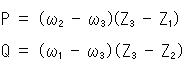
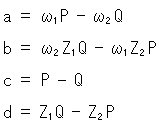
 Fig.16をご覧ください。
Fig.16をご覧ください。 Fig.17をご覧ください。
Fig.17をご覧ください。 Fig.18をご覧ください。
Fig.18をご覧ください。 Fig.19をご覧ください。
Fig.19をご覧ください。

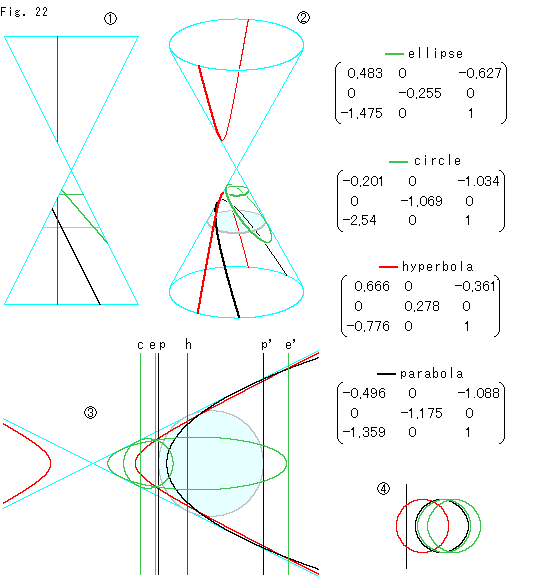 Fig.22をご覧ください。
Fig.22をご覧ください。
