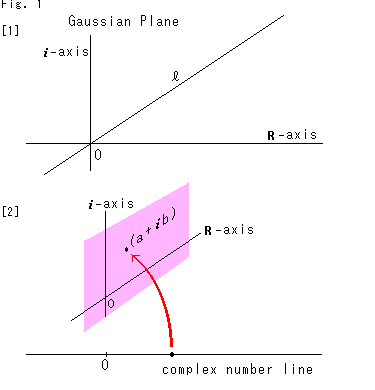
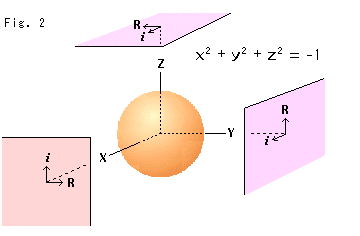
 Fig.2'をご覧ください。
Fig.2'をご覧ください。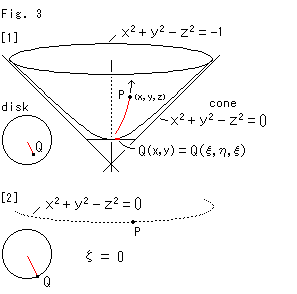 Fig.3をご覧ください。
Fig.3をご覧ください。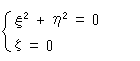
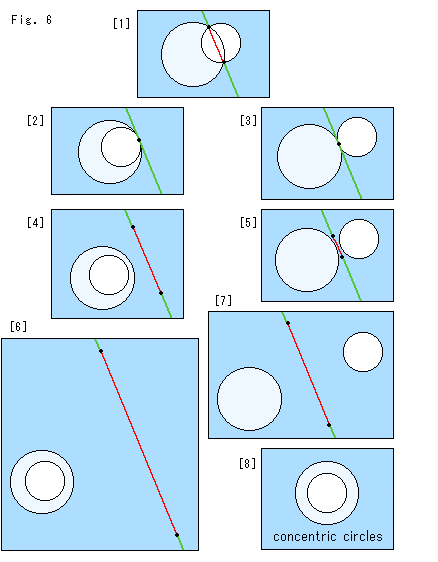
 Fig.4のように、円や楕円は交わることもあれば交わらないこともあります。 楕円が他の楕円と交わると、交点が4つできる場合があります。 交わるのが円と円のときは、交点が2つできます。 ところが、ポンスレ―は「どんな2つの円も、つねに4つの交点で交わっている」というのです。 それなら、円を楕円と区別することなく公平ですし、交わるとか交わらないといった不連続もありません。 円が2つあれば、どんなに離れていても、いつも交わっているのです!
Fig.4のように、円や楕円は交わることもあれば交わらないこともあります。 楕円が他の楕円と交わると、交点が4つできる場合があります。 交わるのが円と円のときは、交点が2つできます。 ところが、ポンスレ―は「どんな2つの円も、つねに4つの交点で交わっている」というのです。 それなら、円を楕円と区別することなく公平ですし、交わるとか交わらないといった不連続もありません。 円が2つあれば、どんなに離れていても、いつも交わっているのです!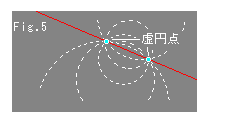
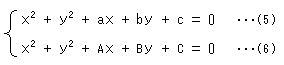
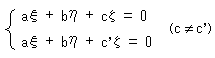
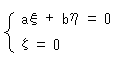
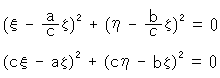
 さらに不思議なことには、この虚直線上の任意の2点間の距離はゼロです。 実際、式(8)は点(
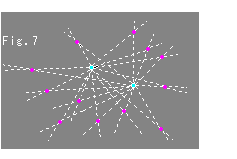
さらに不思議なことには、この虚直線上の任意の2点間の距離はゼロです。 実際、式(8)は点(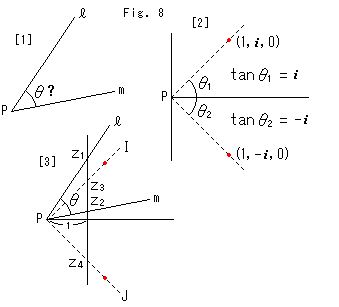 Fig.8をご覧ください。
Fig.8をご覧ください。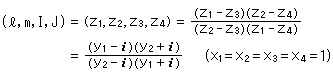
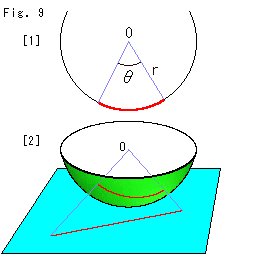 と虚実に分けてみると、
と虚実に分けてみると、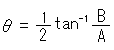
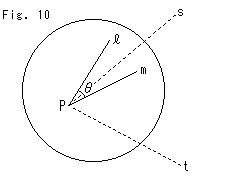 Fig.10をご覧ください。
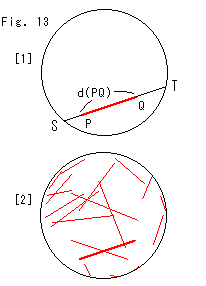
Fig.10をご覧ください。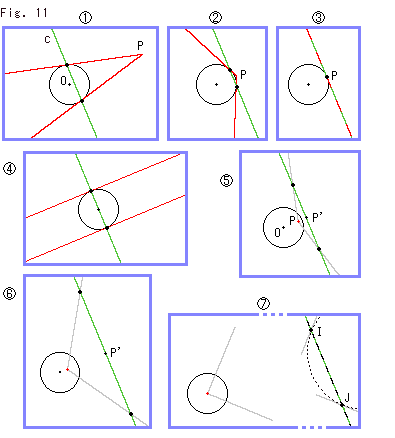 Fig.11をご覧ください。 円の実と虚の接線のからみぐわいを見ていきます。
Fig.11をご覧ください。 円の実と虚の接線のからみぐわいを見ていきます。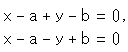
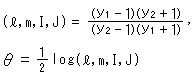
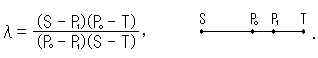
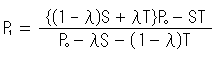
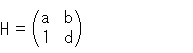
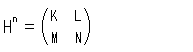
|
ユークリッド平面を無限の広がりをもったものだとすると、自然に射影平面に なります。 双曲幾何の円板モデルは開円板です。それは、円板から円周を取り除いた ものだと考えられます。その円板の内部では、いくらでも遠いところへ行け るけれども、無限遠へは行けない。つまり、円板の内部では、どんな長さも 有限だということになります。(理想三角形の頂点などは、実際は先端が欠 けているのだと理解します。) ですから、円板モデルでは対心点の同一視は考えないというよりも、対心点 そのものが存在しないのです。 −−−−と考えます。 質問: 1. 上の考え方は正しいでしようか。 2. 極限についてです。 左辺は、Xがaに限りなく近づいた挙句の果てということです。Xはaにいくら でも近づきはしますが、近づくだけです。たとえ、挙句の果てであっても、 Xとaとの間には隙間があります。けっして とはなりません。ですから、 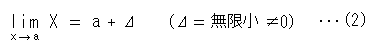
と書くべきです。(1)が許されるのは、そうだとしても差し支えないときに限 ります。 この考えは正しいでしようか。( 開円板の内部から円周へ向かって進むときは、(2)に拠らなければなりま せん。いかがでしようか。 
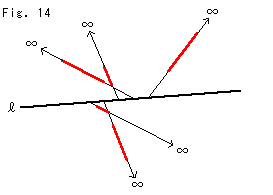
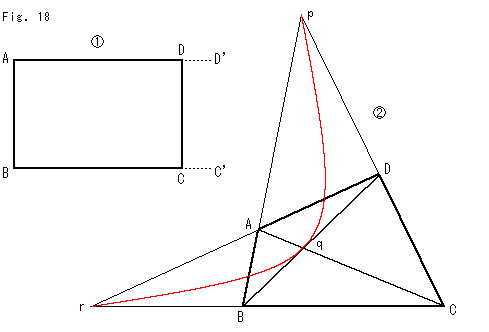
3. 理想三角形の頂点は、円板モデルの円周上 にあるのですから、そこでは対心点の同一視 が作用します。すると、3辺を延長することが できます。 その結果は右図のようになるの でしようか。 回答: いくつかの難しい問題も含んでおり、即答できま せん。が、わかる範囲で答えます。 まず、無限遠に発散することを一般に のように書きます。(infinity = 無限大) これは、「無限遠点の近傍」という概 念があるからです。もちろん通常の距離空間ではこうはなりません。 (任意の点と無限遠点との距離は無限大だから。)ですから、無限遠点を点 として考えるとき、その近傍系を何らかの形で定義するのであれば、普通の 位相空間としての収束がありえます。 双曲幾何学を射影空間へ拡張して考えてみたいとのことですが、できるは ずです。ただ、無限遠点の対蹠点を同一視する、というような方法ではない ような気がします。ユークリッド平面の場合には、一つの直線の両端が同じ 無限遠点である、という解釈ですべてが説明できます。双曲平面の場合に はそれができません。ですから、射影平面への拡張は違う方法だと思いま す。しかし、残念ながら私はその方法を知りません。いつかわかったらお知 らせします。 |