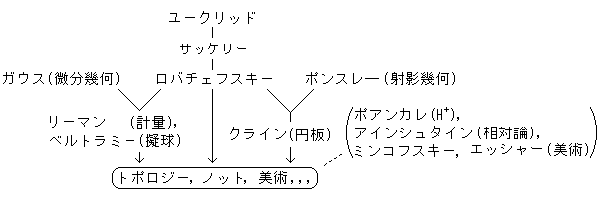
|
・無限大は、定義しだいだ。 あるいは、無定義語としておくのが よいかもしれない。 無限遠は、何処ということができないばか りでなく、どの方向かを指すこともできない。 想うことも禁じられる。 想えば、その向こうも想えるからだ。 でも、人間はそれを想うことができる。 いずれにしても、物理的な無限遠を数学的な対象にすることは､ 不可能である。 ・射影幾何では、無限遠を定義はせずに、その扱い方を規定す ることで手中のものとしている｡ ・モデルは、双曲幾何を完全にシュミレートするが、無限遠その ものは別である。 ・モデルでなく実物を自分の目で見たい気持ちが、どうしても拭 えない。 誤ったこだわりだけれども。 ・ロバチェフスキーは、彼の公理から完全な双曲幾何を構築した が、無限遠そのものは自分の推測によった。 また、裏付けのない洞察で、双曲幾何は成り立つものだとした｡ ・リーマンは、微視的な計量によって双曲幾何を明らかにした。 その計量を取り変えれば、どの世界も同じように扱える。 しかし、特定の計量を与えるというのは意図的であって、必然 性がない。 ・クラインは、巨視的な変換によって双曲幾何を明らかにした。 その変換を選ぶことで、いろいろな世界も同じように扱える。 ・トポロジストは、身近に双曲幾何のモノがあることを示した。 |
|
双曲幾何の生い立ちには、 (1) 公理の否定から、 (2) 計量の考え方から、 (3) 変換群（射影幾何）の考え方から の三つのルートがる。 |
でなく720だけ空間を回転したときに元の値にもどることの実験的証明がなされたという話しがあります。 気になりますねえ。
22)。