[前章] [次章] [目次]
第4部 8字ノット
Ch.50 8字ノット(1) 
これから先の話しはトポロジーに関したことです。 双曲幾何の応用例でが、この8字ノット(八の字結び目)というものでは、狂おしいほどの想像力が要求されます。 頭がねじれるかも知れないので、気をつけてください。
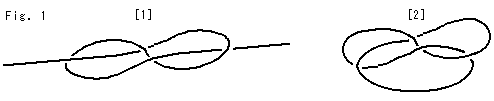 Fig.1をご覧ください。
Fig.1をご覧ください。
[1]: 紐を図のように結びます。
[2]: その両端をつなぐと、8字ノットになります。 それは、自分自身と接触せずに立体交差する3次元のループです。 ループの大きさや形は問いません。 紐といっても、曲線として考えます。 曲線は点の連なったもので、その直径(>0)は点です。 両端が無限に伸びている(無限遠でループになる)ものも8字ノットです。

Fig.2をご覧ください。
[1]: 8字ノットは、よくこのように描かれます。 見る方向や、ほぐし方や絡ませ方によって、さまざまな姿態になりますが、図の格好のものが一番ポピュラーです。
[2]: 針金でつくったものです。
後ろから見ても横から見ても同じです。 垂直方向から見ると、点対称になっています。
[3]: ノットの紐が前後にも曲がっている様子を強調するために、中間にカーテンを降ろしてみたものです。 Elementary Topology に動かして見れる絵があります。
いろいろな言葉が出てきますので、それらを先ず見ておきます。 準備作業です。 といっても、いつものように厳密なことは避けているので、まあこんなものかと読んでおいてください。 正直なところ、筆者にも釈然としないところだらけです。
------トポロジー
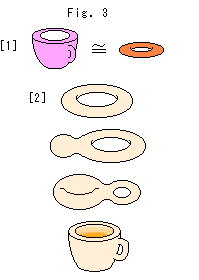 Fig.3をご覧ください。
Fig.3をご覧ください。
トポロジーとは、考え方の一つです。 それを定義するのは難しいですが、すぐに親しくなれます。
[1]: トポロジーでは、コーヒ―カップとドーナツをトポロジー的に同じ(位相同型)だとみます。 どちらにも穴が1つあるからです。 記号“ ”は、たがいに位相同型であることを表わしています。 でも、ふつうの等号“=”がよく使われています。 位相同型のもとでは、ちぎったり、貼ったりしないかぎり、どのように変形してもかまいません。 そも、定まった形とか大きさや場所というものを考えないのです。 射影幾何より自由です。 トポロジーでも、ものを点の集合として考えます。 ですから、位相同型を保つには、連なっていたものを離したり、離れていたものをつないではいけません。 それは、ゴムのシートに描かれた地図のようなものです。
”は、たがいに位相同型であることを表わしています。 でも、ふつうの等号“=”がよく使われています。 位相同型のもとでは、ちぎったり、貼ったりしないかぎり、どのように変形してもかまいません。 そも、定まった形とか大きさや場所というものを考えないのです。 射影幾何より自由です。 トポロジーでも、ものを点の集合として考えます。 ですから、位相同型を保つには、連なっていたものを離したり、離れていたものをつないではいけません。 それは、ゴムのシートに描かれた地図のようなものです。
[2]: いま、ドーナツがやわらかい粘土でできているとします。 すると、ちぎったりつないだりすることなくコーヒ―カップに変形できます。 そのとき、粘土を捏ねたり組成粒子(点)をかき混ぜたりしなければ、変形中ずっと位相同型が保たれています。
つまり、前後で1対1の連続した写像になっていれば、位相同型であるというのです。 それは、前後を比べるときにそうであればよいのであって、途中経過については問いません。
ルールとして、
“隣接点は隣接して、離れた点は離れて”
ということが守られていれば、よいのです。 これを位相同型ルールと名付けておきます。
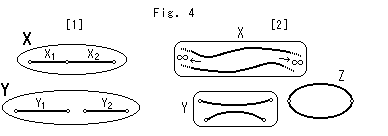 Fig.4をご覧ください。
Fig.4をご覧ください。
コーヒーカップとドーナツの話しはポピュラーですが、それとは少し趣きのちがうことでの位相同型ルールについて見ておきます。
[1]: 線分を点の集まりとした集合で考えます。 太い黒い線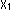 ,
,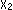 ,
,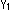 ,
,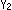 は線分で、
は線分で、 印しは開端点であることを表現しています。 このとき、
印しは開端点であることを表現しています。 このとき、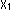 と
と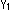 は位相同型です。
は位相同型です。 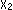 と
と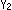 も位相同型です。 ところが、
も位相同型です。 ところが、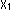 と
と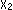 の全体をXとし、
の全体をXとし、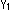 と
と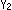 の全体をYとすると、XとYは位相同型ではありません。
の全体をYとすると、XとYは位相同型ではありません。 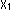 と
と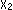 は
は を挟んでくっついていますが、
を挟んでくっついていますが、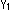 と
と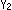 はそうはなっていないからです。
はそうはなっていないからです。
[2]: Xの中には無限に伸びた2つの曲線があります。 この2曲線は無限に伸びているので、端がなく開端点になっています。 ですから、XとYは同相です。 Z も2本の曲線ですが、 を挟んでくっついているので、2曲線はたがいにタッチしていないけれども、XやYとは位相同型ではありません。
を挟んでくっついているので、2曲線はたがいにタッチしていないけれども、XやYとは位相同型ではありません。
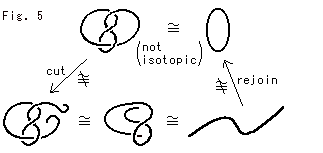 Fig.5をご覧下さい。
Fig.5をご覧下さい。
ノット(結び目)とループは同相(位相同型)ですが、同位(isotopic)ではありません。 両者は、どんなに変形しても、ちぎって継ぎ直すことでもしないかぎり、合同にはなりません。 それでも、両者はともに3次元のループなので、位相同型です。 また、位相同型であるかどうかは、判断をするその時点でのことです。 そのとき、ちぎったところが、元のようにつながれていることに注意してください。 切断されている間のノットは、もとのノットと位相同型ではありません。
同位というのは、1つの空間におけるものです。 ユークリッド空間と双曲空間といったような別個の空間にあるものが同位かどうかをいうことはできません。 このFig.5では、ノットとループが同じ空間にあることを前提としています。 しかし、位相同型は、比べるものが同一の空間になくてもよいのです。 抽象的な空間であってもかまいません。
------ 境界と開端点
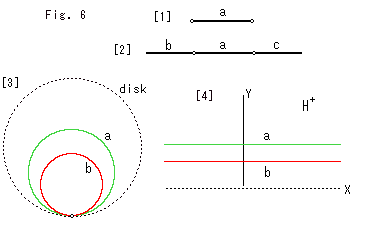 Fig.6をご覧ください。
Fig.6をご覧ください。
[1]: aは両端が開かれた線分です。 このようなものが単独に在るとき、つまり、その外界を考えないとき、境界はありません。 境界は内在的なものではないといわれています。
[2]: aの両側にはbとcがあります。 つまり、X  Y といった関係になっています。 このような場合にかぎって、境界をいうことができます。 aの両端の
Y といった関係になっています。 このような場合にかぎって、境界をいうことができます。 aの両端の 印しのところが境界なります。
印しのところが境界なります。
[3]: aとbはポアンカレ円板上のホロサイクルです。  印しのところは、開になっています。 これまでとはちがって円板の周を点線で描いています。 それは、円板モデルには端がなく外界もないので、境界がないからです。 そのため、本当は周を描いてはいけません。 しかし、それではモデルとしての視覚的なたすけにならないので、点線にたよったものです。
印しのところは、開になっています。 これまでとはちがって円板の周を点線で描いています。 それは、円板モデルには端がなく外界もないので、境界がないからです。 そのため、本当は周を描いてはいけません。 しかし、それではモデルとしての視覚的なたすけにならないので、点線にたよったものです。
この図を見ていると、ホロサイクルaとbの間隔が点 へ近づくほど狭くなって、点
へ近づくほど狭くなって、点 のところでは、aからbへつたって行けるように見えますね。 しかし、aとbの間の距離はどこでも一定であることを既につかんでいます。
のところでは、aからbへつたって行けるように見えますね。 しかし、aとbの間の距離はどこでも一定であることを既につかんでいます。
[4]: ホロサイクルa,bを上半平面 に移したものです。 X軸を点線で描いてあるのは[3]と同じ考えです。 これで見れば、ホロサイクルaとbはあきらかに別個のところを走っています。 1個の開端点
に移したものです。 X軸を点線で描いてあるのは[3]と同じ考えです。 これで見れば、ホロサイクルaとbはあきらかに別個のところを走っています。 1個の開端点 を2つの曲線が共有していても、このようになっている場合があることには驚かされますね。
を2つの曲線が共有していても、このようになっている場合があることには驚かされますね。
朝の を想いましよう。 私たちのコーヒーカップの中に、いま全宇宙が入っているんですよ! コーヒーの中の点も全宇宙の点も、無限個あって、1対1で連続して対応づけできるはずですから。 ただし対応づけた後では、かき混ぜないで、そっと飲んでください。 コーヒーだけに注目しているときには、その外側のことは考える必要はなく、コーヒーを全宇宙だとしてよいわけです。 そうだとすると、コーヒーカップが目に見え手にとれるのはヘンですね。 いや、コーヒーは私たちの空間に埋められたのだから、その外側を考えてもよく、コーヒーカップはその境界だといえます。 でも、なんだかおかしいですね。 カントールの集合論のようなことは考えていません。 ごく素朴にいきましよう
を想いましよう。 私たちのコーヒーカップの中に、いま全宇宙が入っているんですよ! コーヒーの中の点も全宇宙の点も、無限個あって、1対1で連続して対応づけできるはずですから。 ただし対応づけた後では、かき混ぜないで、そっと飲んでください。 コーヒーだけに注目しているときには、その外側のことは考える必要はなく、コーヒーを全宇宙だとしてよいわけです。 そうだとすると、コーヒーカップが目に見え手にとれるのはヘンですね。 いや、コーヒーは私たちの空間に埋められたのだから、その外側を考えてもよく、コーヒーカップはその境界だといえます。 でも、なんだかおかしいですね。 カントールの集合論のようなことは考えていません。 ごく素朴にいきましよう
------ 幾何
これからあとは、幾何という言葉をトポロジーと対比的な意味で用います。 その幾何は2つの意味を含んでいます。 一つは、ものを測ることで、もう一つは、距離(計量)を保つことです。 距離を保つとは、どこでも長さをきっちり測れるということです。
------ 次元
トポロジ―では、曲線は1次元、曲面は2次元、(中身の詰まった)立体は3次元だといいます。 どう歪んでも次元は変わりません。 いいかえると、ものがどんな空間を占めるかよりも、ものそのものの方に注目するのです。 ものに長さだけがあれば、1次元。 ものに広がりだけがあれば、2次元。 ものに広がりと深さだけがあれば、3次元。 と、いうぐあいです。 3次元は、ふつうに縦・横・高さと考えてよいのですが、中身の詰まったものは、それ自体をとらえて3次元といい、どんなにかさばっても、空に浮かんだバルーンのように外皮だけなら2次元といいます。
空間は3次元以上とは限りません。 縦・横・高さといった広がりはなくてもよいのです。 曲面は2次元の、曲線は1次元の空間です。 そして、点はゼロ次元の空間と捉えます。 多様体とよばれるものも空間です。 トポロジーでは、よくモノとそれがおかれている空間を別個に考えます。
------ 同一視
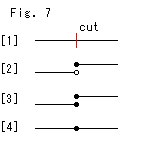 Fig.7をご覧ください。
Fig.7をご覧ください。
同一視というのは、トポロジーでよく使うテクニックです。
[1]: 曲線を切ったとします。
[2]: 一方の切断端を開端点とすると、他方の切断端は閉端点です。 これが、ふつうの考え方ですね。
[3]: しかし、トポロジーでは、両方の切断端を両者で同一視します。 1つのものを2つにしたのではなく、たがいにコピーになっているというのでもありません。 べつべつのものを1つの同じものだとするのです。 開とか閉とかいったことは、別に考えます。
[4]: 同一視によって、ふたたび接続したところです。 ふたたびといいましたが、図[4]と図[3]は同じことを表わしているのです。 面と面についても、同様です。 どんな次元のものにも適用できます。
------ ドーナツ(トーラス)
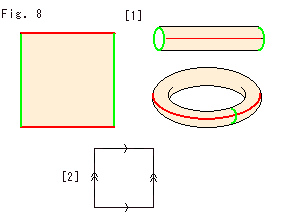 Fig.8をご覧ください。
Fig.8をご覧ください。
[1]: 四角形をゴム膜のようなものだと考えます。 円筒状にして両端を貼り合わせると、トーラス(ドーナツ形の面)が得られます。 四角形は、トーラスを作るだけなら、どんな形のものでもかまいませんが、正方形にしておくと都合のよいことがあるので、それにしておきます。 貼り合わせるときは、歪んでもかまいませんが、捻らないで赤い線と赤い線、緑色の線と緑色の線とをきっちり合わせてください。 捻ってつなぐと、あのメビウスの帯に似たことが起こるからです。
トーラス上では、正方形の4つの隅が1点に集められて、緑と赤の辺で区切られた4つの面が滑らかにつながっています。 そこでは4つの隅の角の和がちょうど2 (90
(90 ×4)になって、隙間もしわもありません。
×4)になって、隙間もしわもありません。
[2]: この貼り合わせ約束(同一視)を、もとの正方形の辺に矢印しを入れたもので表現します。 ドーナツ面とこの矢印し付き正方形は、見た目に形は違いますが、[1]と位相同型です。
簡単のために、ここでは印し付き正方形をたんに正方形とよぶことにします。
正方形の中ではユークリッド幾何が成り立つとします。 いいかえれば、成り立つのは当然ではなくて、私たちが正方形をユークリッド空間にセットする(埋め込む)のです。 すると、
2-トーラスはユークリッド幾何をもつ
というのです。 わかりにくい話ですね。 でも、おいおい慣れてきます。
“2-”は面であることを明示したものです。 2-トーラスはチューブの輪のようなものですが、中身が詰まっていても表面だけを考えればよいのです。 3-トーラスというのもありますが、それはチューブの中が詰まった輪ではありません。 正方形でなく、立方体の面と面を抽象的に貼り合わせたものです。
オイラー数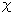 を計算してみると、トーラスは頂点が1つ、辺が2つ、面が1つですから、
を計算してみると、トーラスは頂点が1つ、辺が2つ、面が1つですから、
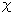 = v - e + f
= v - e + f
= 1 - 2 + 1 = 0 .
オイラー数 が 0 だと、ユークリッド的だといわれています。
が 0 だと、ユークリッド的だといわれています。
2-トーラスがユークリッド的であることは、オイラー数をもち出さなくても、こう考えられます。 輪の穴のある方の面は、曲率-1の鞍形に似ている。 穴と反対側の方の面は、曲率+1の球面に似ている。 全体の曲率は、差し引き 0 だ。 だから、トーラスはユークリッド的だ、というぐあいです。
------ 抽象的貼り合せ
正方形を貼り合わせてトーラスを作るには正方形を歪めないとできませんが、そうはしないで、正方形のままで抽象的に貼り合わされてあるモノを考えます。 それは、まったく抽象的ですから、描くことはできませんが、想うことはできます。
正方形は、抽象的な貼り合せ約束をもったものであるだけでなく、抽象的なモノを(実際には不可能だけれども、あえて)具象化したものともいえます。 ドーナツ面は、無理やりに物理的な貼り合わせを実行したものです。 無理やりというのは、正方形を歪めていることです。 抽象的貼り合せでは、けっして歪みをつくることはありません。 いいかえれば、形が定められているときは、それを保つということです。
見えないというのは、外観が見えないことです。 内部に入って見るとか、スライスして次元を下げて見ることができる場合があります。ですから、ふつうに見えないというときは、外観の方を指しています。
ところで、ユークリッド空間を外から見たことがありますか? いいえ、誰にもできません。 私たちは、その中だけを見ているのです。 ユークリッド空間も開空間とみられています。 そうすると、イヤそうでなくても、私たちがユークリッド空間の外に出るとか、外から見る話しはナンセンスですね。
ちなみに、地球儀は地球を外から見たように描かれています。 そして、天球儀も天球を外から見たように描かれています。 つまり、宇宙を宇宙の外から見ているのです。 星座早見盤のように、天を仰いだ眺めとは逆になっています。 宇宙を手元に反転したような感じです。 また、裏返した宇宙になっているともいえます。 星座早見盤にも、ふつうと違うところがあります。 ふつうの地図の東西とは逆に、北を上にして見ると右が西で左が東になっています。 天体望遠鏡なんかも、上下逆に見えるものがほとんどのようです。 さらに、万華鏡などは、1つのものを沢山にして見せていますね。 右の写真は、大きな万華鏡の中へ入って写したものです。 3人の自分が背中をつき合わせていますし、遠くの自分がこの自分を見つめています。
ともかく、具体的に見るといっても、こんな風にいく通りも考えられます。 そして、ときには抽象的貼り合せで想う方が、やさしいことすらあります。
------ 一般呼称
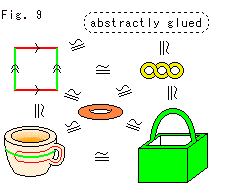 トポロジーの観点から、正方形とドーナツ面と抽象的に貼り合わされたモノの三者を1つのことばでトーラスとよびます。 2次元であることを強調する場合は、2-トーラスといいます。
トポロジーの観点から、正方形とドーナツ面と抽象的に貼り合わされたモノの三者を1つのことばでトーラスとよびます。 2次元であることを強調する場合は、2-トーラスといいます。
トポロジストたちは、区別のない語を使います。 たとえば、Fig.9にはコーヒーカップ、ドーナツ、正方形などがあります。 点線で囲んであるのは抽象的に貼り合せた(abstractly glued)モノです。 コーヒーカップの赤と緑の線は正方形の辺に対応しています。 これらのすべてをトポロジストたちは、よく一語でトーラスとよびます。 位相同型だからです。 しかし、私たちは、こんな言い方には慣れていないので、気をつけねばなりません。
筆者自身、彼らが話すとき、なんでもかでもトーラスだといっているように感じて、戸惑います。
抽象的に貼り合わされたモノも、もちろん位相同型です。 まったく歪めずに貼り合わされているのですから。
------ 正八角形
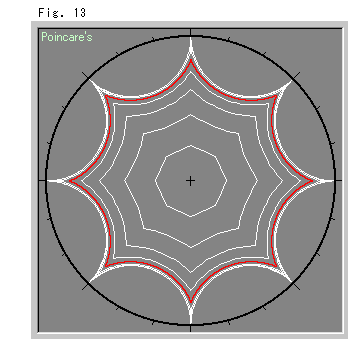 つぎは、正八角形です。 双曲幾何の出番です! 双曲幾何が導き出されるのではありません。 双曲幾何が成り立つ平面に正八角形を埋めるのです。
つぎは、正八角形です。 双曲幾何の出番です! 双曲幾何が導き出されるのではありません。 双曲幾何が成り立つ平面に正八角形を埋めるのです。
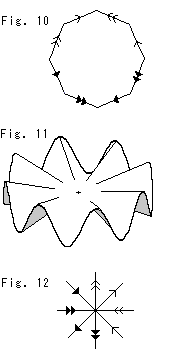
Fig.10の矢印し付き正八角形を用意します。 いつものようにゴム膜だと思って、同じ印しの辺どうしを貼り合わせて滑らかな曲面をつくります。 しかし、このままでは巧くいきません。 8つの頂点が1点に集まるときに、Fig.11のように、内角の和が2 を超えて皺になってしまうからです。 8つの隅が、Fig.12のように、ぴったりと集まらなければなりません。 各内角を狭めて、皺にならないようにするには、どうすればよいでしようか。
を超えて皺になってしまうからです。 8つの隅が、Fig.12のように、ぴったりと集まらなければなりません。 各内角を狭めて、皺にならないようにするには、どうすればよいでしようか。
これをうまくやる方法があるのです。 それは、この正八角形をFig.13のようにポアンカレ円板モデルの真中へ埋めて伸縮します。 すると、赤い曲線で示したように、内角の和がちょうど2 (1つの内角が45
(1つの内角が45 ) になるものが得られます。 円板を単位円とすると、外接円の半径が0.841くらいのところです。 それより正八角形を大きくすると、内角が小さくなって、貼り合わせたところが尖ってきます。 正八角形を小さくすると、内角が大きくなって、貼り合わせたときに皺がよります。
) になるものが得られます。 円板を単位円とすると、外接円の半径が0.841くらいのところです。 それより正八角形を大きくすると、内角が小さくなって、貼り合わせたところが尖ってきます。 正八角形を小さくすると、内角が大きくなって、貼り合わせたときに皺がよります。
図は正八角形の外接円の双曲半径を等間隔にとって、頂点が円板の周に達しようとするまで描いてあります。 一番外側の辺が太く見えるのは、そのためです。 ポアンカレ円板をつかったのは、角が見た通りになるからです。 クライン円板ても、上半平面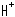 でも、要するに双曲平面であればよいのです。
でも、要するに双曲平面であればよいのです。
矢印しが付いていて、内角が45 である双曲正八角形を、たんに双曲正八角形とよぶことにします。
である双曲正八角形を、たんに双曲正八角形とよぶことにします。
このように長さや角をいえるようにすることを幾何化といいます。 また、幾何構造を与えるともいいます。
------ 二人乗り浮き輪
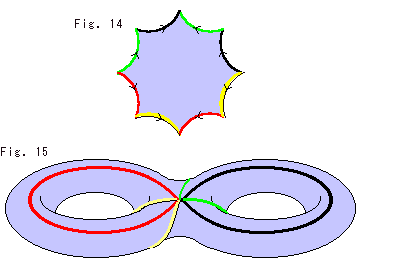 Fig.14は、辺に色をつけた双曲正八角形です。
Fig.14は、辺に色をつけた双曲正八角形です。
この双曲正八角形を用いると、Fig.15のように滑らかな二人乗り浮き輪の面ができます。
二人乗りの浮き輪をよく見ると、赤緑黒黄の線のどれも横切らないで好きなところへ這っていけます。 それは、Fig.14から作ったのですから当然です。
双曲正八角形の抽象的な貼り合わせは、これまでと同様に、形を変えないで行うものです。 当然、貼り合わせたモノを見ることはできません。 二人乗り浮き輪の面は、それを具現化したものです。
二人乗り浮き輪には、穴が2つあります。 それで、双曲正八角形と、その抽象的な貼り合わせをしたモノと、二人乗り浮き輪の面の三者を総称して、2穴トーラスといいます。
正八角形からつくられた双曲正八角形は、外周の形だけでなく、内側の面も双曲的です。 つまり、たんなる変形ではなく、双曲的なものへと質的に変わっているのです。 もとの正八角形がユークリッド的なものだとは言ってないのですから、変わったとするよりも、双曲幾何を与えたとする方がふさわしいですね。 いずれにしろ、双曲正八角形上では、双曲幾何が成り立つので、2穴トーラスは双曲幾何をもつといいます。 二人乗り浮き輪でなくて、メガネの縁であっても話しに変わりはありません。
ここでちょっと、言葉づかいに注意しておくべき点があります。 幾何化というのはFig.13のような操作をきっちりしすることであって、二人乗り浮き輪をつくるときは、そこで得られた八角形をふたたびゴム膜のように扱っているということです。
オイラー数 を計算してみると、2穴トーラスは、頂点が1つ、辺が4つ、面が1つですから、
を計算してみると、2穴トーラスは、頂点が1つ、辺が4つ、面が1つですから、
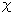 = v - e + f
= v - e + f
= 1 - 4 + 1 = -2 .
です。 オイラー数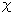 が負ですから、双曲的です。
が負ですから、双曲的です。
この場合もオイラー数をつかわずに、穴の数をかぞえて鞍形的な面のところが2つ、球面的な面のところが1つだから、差し引き曲率-1で双曲的だ。 と、つかめます。 Fig.15を見ると、2つの浮き輪がつながったところが鞍形状になっていますが、膨らませば消えてしまいます。 そんなふうになるところは数に入れないのです。
双曲正八角形だけを見て、それから二人乗り浮き輪の面ができるのを直ぐに見通すのはむずかしいですね。
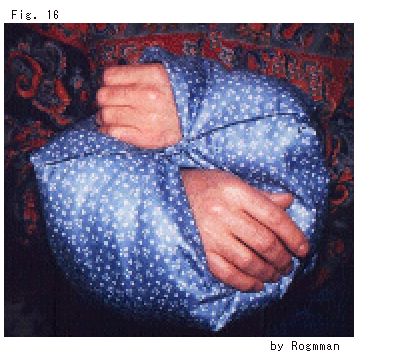
Fig.16は、ログマンが、布をふつうの正八角形に切って、縫い合わせ二人乗り浮き輪の面にして、できた2つの穴のそれぞれに手を通しているところです。 双曲正八角形ではないので、8つの頂点を集めたところは1080 の広がりになりますが、布ですから縫い合わせることができます。 その作り方を見ると面白いですよ。
の広がりになりますが、布ですから縫い合わせることができます。 その作り方を見ると面白いですよ。
ちょっと考えると、不思議ですね。 布の周りを全部ぬい合わせたのに、穴があくなんって。 みなさんは、頭の中で縫い合わせができますか。
8字ノットを見に行く前に、いくつかのことをもう少し見ておきましよう。
[前章] [次章] [目次]
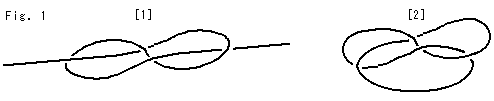

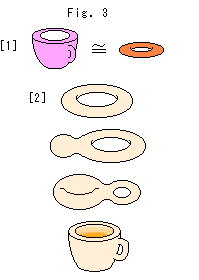 Fig.3をご覧ください。
Fig.3をご覧ください。 Fig.4をご覧ください。
Fig.4をご覧ください。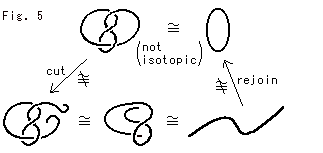 Fig.5をご覧下さい。
Fig.5をご覧下さい。 Fig.6をご覧ください。
Fig.6をご覧ください。 Fig.7をご覧ください。
Fig.7をご覧ください。 Fig.8をご覧ください。
Fig.8をご覧ください。
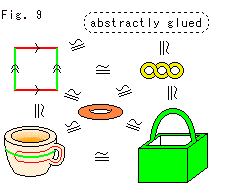 トポロジーの観点から、正方形とドーナツ面と抽象的に貼り合わされたモノの三者を1つのことばでトーラスとよびます。 2次元であることを強調する場合は、2-トーラスといいます。
トポロジーの観点から、正方形とドーナツ面と抽象的に貼り合わされたモノの三者を1つのことばでトーラスとよびます。 2次元であることを強調する場合は、2-トーラスといいます。
 つぎは、正八角形です。 双曲幾何の出番です! 双曲幾何が導き出されるのではありません。 双曲幾何が成り立つ平面に正八角形を埋めるのです。
つぎは、正八角形です。 双曲幾何の出番です! 双曲幾何が導き出されるのではありません。 双曲幾何が成り立つ平面に正八角形を埋めるのです。 Fig.14は、辺に色をつけた双曲正八角形です。
Fig.14は、辺に色をつけた双曲正八角形です。