第4部 8字ノット
Ch.51 8字ノット(2) 
ここでは後の話しのために、空間を考える上でのいくつかのことに触れておきます。 8字ノットと直接には関係しないけれども、役立つと思われるものも取り上げておきます。
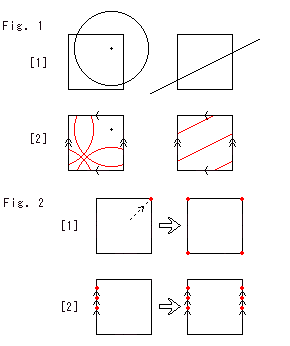 Fig.1をご覧ください。
Fig.1をご覧ください。
トーラスの上を這っていくと、どんな様子が見れるでしようか。 穴の周りをめぐるか穴を通り抜ければ、元のスタートラインへ戻ります。 矢印つき正方形では、右へ進んで行って右側の辺に突き当たろうとすると、左側の辺の同じところから現れて、また右へと進むことになります。 打ち上げたボールは、頭上の辺で跳ね返ることなく、足元の辺から出てきます。 この正方形は有限に見えますが、行き止まりはないのです。
[1]: ふつうの正方形に円や直線を描いたものです。 円も直線も正方形からはみ出しています。
[2]: それを矢印つき正方形で行った場合です。 この正方形は歪められていないことに注意してください。 ゴム製ではありません。 左図は円ですが、その中心は動いていません。 領域の一端にくると境界の他の点から現れるのは、射影平面に似ていますが、まったく別の話です。
Fig.2をご覧ください。
特別な場合です。
[1]: 点がちょど1つの隅に触れたとき、4つの隅に同時に現れるのを描いたものです。
[2]: 点が1つの辺の上を動くとき、反対側の辺にも現れて、同時進行する様子です。
いずれの場合も、1つの点が2つとか4つになったのではなく、あくまで1つのものです。
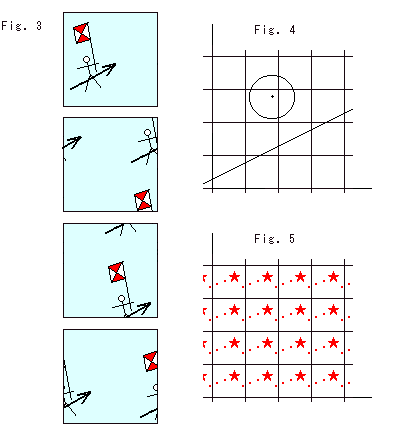
Fig.3をご覧ください。
正方形の上で走る騎士をコマ撮り漫画にしたものです。 彼はあたかも分断されて見えますが、けっして姿を消しません。 どんなに遠くへ行っても。
Fig.4をご覧ください。
格子は、どの位置も各マス目の中だけで測る約束をしたものです。 つまり、無限個の印し付き正方形を敷き詰めたものです。 そうすると、円も直線もふつうに描いて、1つの印し付き正方形の中に描いたのと同じことを表わすことができます。
Fig.5をご覧ください。
この格子は、Fig.4と同じですが、考え方がちがいます。 トーラス上の住人は、その面が世界であって、どこへ行くときも、その面から離れることはありません。 どちらの方向へ旅をしても、出発地と同じところへ着きます。 そこを過ぎて、さらに進むと、また出発地と同じところへきます。 ということは、トーラス上では自分の向こうに自分の背をみることになります。 図の格子でいえば、同じ人物やものが、どのマス目にもいて、動くものは同じ動きをします。 Fig.5は、そいう彼らにとって、世界がどう見えるかを表わしています。 いま、 が一斉に動いたところです。 トポロジストたちは、こんな格子のマス目を基本領域とよんでいます。
が一斉に動いたところです。 トポロジストたちは、こんな格子のマス目を基本領域とよんでいます。
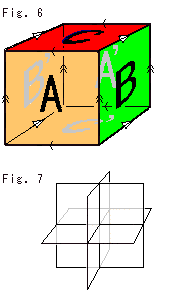 Fig.6をご覧ください。
Fig.6をご覧ください。
こんどは立方体です。 この立方体は中が詰まった3次元です。
立方体の面の向きが、辺に入れてある矢印の4つで表わされています。 向かい合った面と面をそれぞれ同一視するもので、外側と外側を貼り合せします。 この貼り合わせ約束付き立方体をたんに立方体とよぶことにします。
立方体の各面を印しの通りに貼り合わせることは、ふつうにはできませんので、抽象的に頭の中でおこないます。 ただし、SF小説のような4次元の世界で貼り合わせると考えてはいけません。 あくまで、3次元でのことです。 また、正方形がドーナツ"面"になることから、立方体は目に見えるドーナツ"体"になると即断してはなりません。
Fig.7をご覧ください。
この抽象的な貼り合わせでは、8つの頂点のすべてが1点に集まります。 それは、曲げたり捻ったりしせずに思考上で実行する貼り合わせで、矢印とその向きを一致させる約束にしたがえば、8つの頂点が1点に集まるということです。 曲げもしないで1点に集めるとは、不合理に思えますね。 でも、そこが抽象的にというヤツです。 そうして、立方体の8つの隅を隙間もしわもなく、ぴったりと合せることができます。
立方体と、この抽象的に貼り合わせたモノを総称して、3-トーラスといいます。
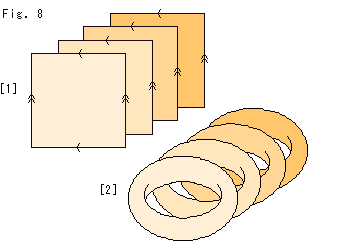 Fig.8をご覧ください。
Fig.8をご覧ください。
抽象的に貼り合わせたモノは3次元ですけれども、描けません。 2-トーラスでは、ドーナツ面という具現化したものがありますが、3-トーラスでは、そんなものはないのです。4次元の世界へ行けば見れるはずですが、それは不可能です。
でも、どこまで視覚化できるか、やってみましよう。 スライスすると次元を下げることができます。 抽象的に貼り合わせたモノをスライスできるとよいのですが、手掛かりがありません。 そこで、先に立方体をスライスして、それを貼り合わせることを考えます。
[1]: 立方体をその面に平行に無限に薄くスライスすると、立方体の向かい合った面から面までの無限枚の正方形になります。
[2]: その一枚ずつをドーナツ面にしたものです。 このあとは、無限個のドーナツの面と面をすべてを重ねればよいのですが、もう物理的にはできません。 それに、形を歪めているので、抽象的に貼り合わせたモノからはなれています。 それでも、すこしはイメージしやすいですね。
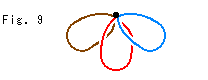 抽象的な貼り合わせの結果は、頂点が1つ、辺が3つ、面が3つの奇妙な立体になります。
抽象的な貼り合わせの結果は、頂点が1つ、辺が3つ、面が3つの奇妙な立体になります。
Fig.9は、それを強いて描いてみたものです。
立方体を、2-トーラスと同様に、ユークリッド空間に埋め込みます。 すると、
3-トーラスはユークリッド幾何をもつ
といえます。
それは、8つの隅がそのままでぴったり合うからです。 Fig.9を見たのでは、かえって混乱しますね。 それよりも、立方体を見て想うほうがよいでしよう。
3次元の(面でなく中身の詰まった)もののトポロジー的性質を判別するオイラー数のようなものは、ありません。
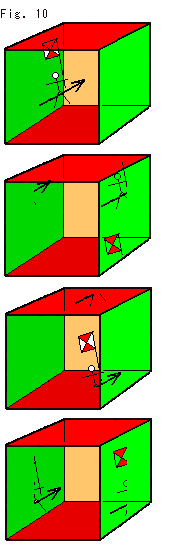
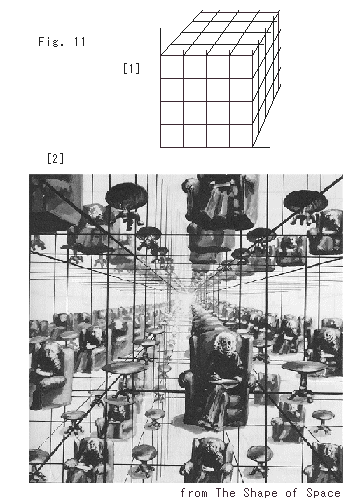 Fig.10をご覧ください。
Fig.10をご覧ください。
立方体を半透明にして中で騎士が動くのを4コマ撮りにしたものです。 右壁に突き当たれば、左壁から現れます。 彼の旗を見てください。 それが天井にとどくと、床下から出てきています。 これは、抽象的に貼り合わせてあるとしたモノの中に入って“見たもの”です!
Fig.11をご覧ください。
[1]: 立方体の3-Dタイル貼り(ブロック積み)です。
[2]: その中にアインシュタインが座っているところです。 無限に多くの彼がいるように見えますが、本当は一人です。 つまり、すべて同一人物なのです。 彼は自分の背も頭上も足の裏も眺めることができます。
星空を観測して、もし、同じものが繰り返し認められたなら、宇宙の姿は3-トーラスだといえることになります。 実際、天文学者たちはそれを確かめようとしています。 すでに、いくつかの証拠を捉えたようです。
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
 八角形について、すこし見ていきます。
八角形について、すこし見ていきます。
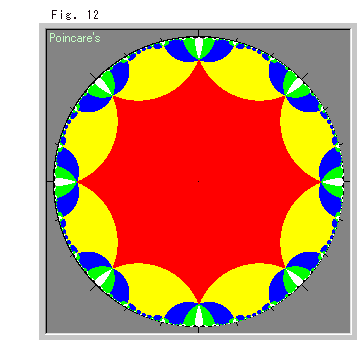
右のFig.12をご覧ください。
双曲正八角形(内角45 )をポアンカレ円板モデルに敷き詰めて着色すると、このような模様になります。 こんどはユークリッド平面ではないので、無限の果てまで描くことができます。 つまり、タイル張りです。 どの頂点も、8つの双曲正八角形に囲まれています。 円板の縁の方にある八角形も、見た目には中央の赤い八角形とちがいますが、すべて内角45
)をポアンカレ円板モデルに敷き詰めて着色すると、このような模様になります。 こんどはユークリッド平面ではないので、無限の果てまで描くことができます。 つまり、タイル張りです。 どの頂点も、8つの双曲正八角形に囲まれています。 円板の縁の方にある八角形も、見た目には中央の赤い八角形とちがいますが、すべて内角45 の双曲正八角形です。
の双曲正八角形です。
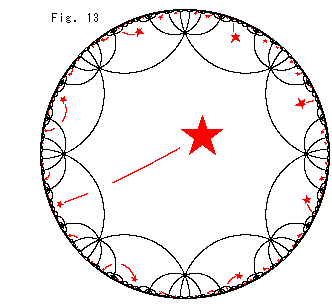
Fig.13をご覧ください。
動く をFig.12の双曲正八角形の中においた場合です。 これは、Fig.5に相当するものです。 全部(無限個)の
をFig.12の双曲正八角形の中においた場合です。 これは、Fig.5に相当するものです。 全部(無限個)の が一斉に動いています。
が一斉に動いています。
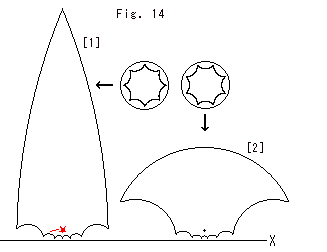
Fig.14をご覧ください。
ついでに、Fig.13の一番大きく見える双曲正八角形を上半平面 に移しててみました。
に移しててみました。
[1]: まるで、発射台のロケットに点火しかけているみたいですね。 (大きさは適当です。) 水平な直線はX軸です。
[2]: ポアンカレ円板上の双曲正八角形を22.5 (π/8)回転して、上半平面
(π/8)回転して、上半平面 上に変換したものです。 黒い点は双曲正八角形の中心です。 [1]とはずいぶん違って見えますが、同じスケールで描いた内角45
上に変換したものです。 黒い点は双曲正八角形の中心です。 [1]とはずいぶん違って見えますが、同じスケールで描いた内角45 の同じ双曲正八角形です。
の同じ双曲正八角形です。
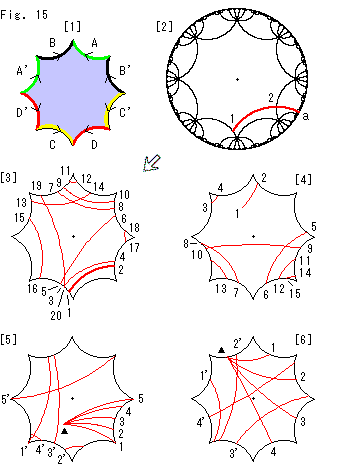
Fig.15をご覧ください。
[1]: 双曲正八角形の、前にも描いた貼り合わせのルールです。
[2]: 双曲正八角形が敷き詰められたポアンカレ円板上に1本の(双曲)直線を引いたものです。 1から出発し、2で辺を横切って、無限個の双曲正八角形を切りながら無限遠である円板の周上の点aへと伸びています。
[3]: [2]の様子を一つの双曲正八角形上で見たものです。 太く描いた赤い曲線 1-2 が、[2]の 1-2 です。 直線と辺との対頂角が等しいことが、同一視された辺どうしで保たれています。 2から3へ移って 3-4 と進み、5-6, 7-8, 9-10,,, 17-18 まで描かれています。 [2]の点aまで伸びている直線を追って、この[3]で描きつづけたら、双曲正八角形のなかは真っ赤に塗りつぶされるでしようか? あとで考えてみます。
[4]: 出発点 1 の場所を変えてみたものです。
[5]: 出発点を双曲正八角形の内部の 印しのところに固定して、1つの辺に向かう角を変えてみたものです。 図は省いていますが、双曲正八角形の中心と頂点を通る直線上赤い直線を伸ばしたとこは、向かい合う頂点に無限回移っていくことになります。
印しのところに固定して、1つの辺に向かう角を変えてみたものです。 図は省いていますが、双曲正八角形の中心と頂点を通る直線上赤い直線を伸ばしたとこは、向かい合う頂点に無限回移っていくことになります。
[6]: こんどは出発点を1つの辺の上の 印しのところに固定して、4つの辺の中点を通るようにしてみたものです。 1は1'へ、2は2'へ、3は3'へというように移っています。
印しのところに固定して、4つの辺の中点を通るようにしてみたものです。 1は1'へ、2は2'へ、3は3'へというように移っています。
いずれも、Fig.1'の右側の図とは様子が大きくちがいます。 双曲的平行線にはなっていません。
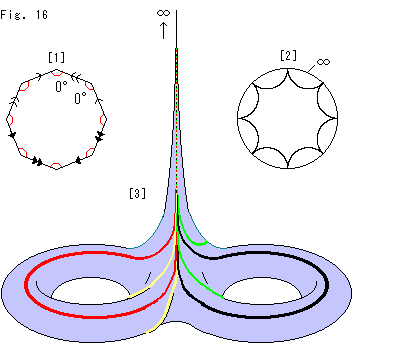
Fig.16をご覧ください。
頂点が円板の周に達している双曲正八角形を理想正八角形といいます。 その辺の長さは無限大で、内角はゼロです。 円板の端は開いているので、実際には、双曲正八角形をいくら大きくしても辺の長さが無限大になることはありません。 理想正八角形というのは、それが実現したとした理想的なものを指しています。 他の理想○○というのも同様です。
[1]: 矢印つきの八角形は、赤い8つの内角がすべてゼロとみなされます。
[2]: ポアンカレ円板上で見た理想正八角形です。 頂点が円板の周上にあるように描かれています。“理想”ですから。
[3]: 八角形の同じ矢印の辺と辺を貼り合わしていくと、尖ったところ(カスプ)のある二人乗り浮き輪ができます。 8つの頂点を滑らかに合わせることはできませんが、頂点はそろって無限の彼方で出会うはずです。
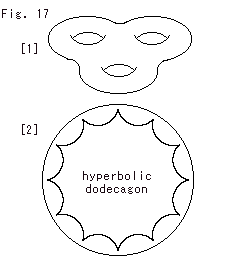 Fig.17をご覧ください。
Fig.17をご覧ください。
数学上では三人乗り以上の浮き輪もあります。 その穴の数を種数といい、ふつうgと表わされています。 穴が1つのトーラスの種数gは1です。 種数ゼロは球面です。 2-トーラスの種数gが2より大きくなると、どうなるのでしようか。
[1]: 種数gが3で、3人乗りの浮き輪です。
[2]: ポアンカレ円板上の双曲正十二角形(dodecagon)です。 どの内角も30 で、ぜんぶの頂点を1点に集めるとちょうど360
で、ぜんぶの頂点を1点に集めるとちょうど360 になります。 どんなに種数gが大きくても、同様です。 つまり、穴が2つ以上ある浮き輪は、ぜんぶ幾何化できるのです。
になります。 どんなに種数gが大きくても、同様です。 つまり、穴が2つ以上ある浮き輪は、ぜんぶ幾何化できるのです。
種数gを使うと、オイラー数 は
は
 = 2 - 2g
= 2 - 2g
と簡単に計算されます。
g > 1 では、 < 0 となるので、
< 0 となるので、
種数gが2以上のすべての2-トーラスは双曲幾何をもつ
ことがわかります。
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
超球面 とよばれるものがあります。
とよばれるものがあります。
それは3-球面ともよばれます。 いったい、何んでしようか。 ふつうに物を考えるとき、それが置かれる空間のことは、あまり意識しません。 というのは、自分もモノと同じユークリッド空間にいるのですから。 しかし、物が存在するのは、それが置かれる空間があってのことですね。 ところが、数学では、ちょっと、ややこしいのですが、空間を定めておく場合と、そうでない場合があるのです。 超球面は、空間の一つです。 私たちの知っている空間は、ユークリド空間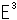 と双曲空間
と双曲空間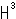 ですが、超球面
ですが、超球面 はユークリド空間に手を加えたものです。
はユークリド空間に手を加えたものです。
3次元ユークリド空間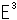 は無限遠点を含んでいるのでしようか。 ふつうの常識では、空間に無限の彼方があるのは当然です。 そんなことを気にもしません。 しかし、数学では無限遠点を含んでいないものとして考えます。 それで、無限遠点を含んでいない
は無限遠点を含んでいるのでしようか。 ふつうの常識では、空間に無限の彼方があるのは当然です。 そんなことを気にもしません。 しかし、数学では無限遠点を含んでいないものとして考えます。 それで、無限遠点を含んでいない とよばれるものと、無限遠点
とよばれるものと、無限遠点 の1つを使います。
の1つを使います。
実は、これまでもそうしてきていたのです。 しかし、注意しなければなりません。 射影幾何では、射影平面を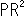 と表わして、射影平面は平面
と表わして、射影平面は平面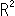 に無限遠点
に無限遠点 を1つ加えたものだといって、
を1つ加えたものだといって、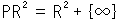 と書いたりします。 ここでの空間は、そんな向きつけ不能といわれるものではありません。
と書いたりします。 ここでの空間は、そんな向きつけ不能といわれるものではありません。
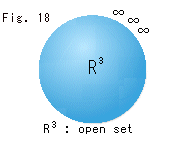 Fig.18をご覧ください。
Fig.18をご覧ください。
 は、いくらでも原点から遠い点をとることはできるが、無限遠点
は、いくらでも原点から遠い点をとることはできるが、無限遠点 は含まない空間です。 ふつう、球形のように空想しますが、その縁は定まっていないので、ハッキリしません。 皮をむいたリンゴのようなもので、開球体とか開集合(open set)とよばれます。
は含まない空間です。 ふつう、球形のように空想しますが、その縁は定まっていないので、ハッキリしません。 皮をむいたリンゴのようなもので、開球体とか開集合(open set)とよばれます。
その外側には、無数の無限遠点 があるはずです。 しかし、場合によって、1個で十分なときは1個と考えます。
があるはずです。 しかし、場合によって、1個で十分なときは1個と考えます。
 の中は見れますが、外から見ることは無限遠まで行かないとできません。
の中は見れますが、外から見ることは無限遠まで行かないとできません。
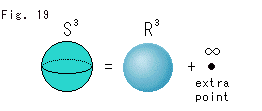 Fig.19をご覧ください。
Fig.19をご覧ください。
 に、その中にはない余分(extra)な1個の点を付け加えたものが超球面で、
に、その中にはない余分(extra)な1個の点を付け加えたものが超球面で、 と表わします。 この余分な点は、
と表わします。 この余分な点は、 の内部に含めない点なら何でもよいのですが、ふつう記号
の内部に含めない点なら何でもよいのですが、ふつう記号 で表わします。 私たちは、それを無限遠点の1つだとしておきます。 その方が分かりやすいからです。
で表わします。 私たちは、それを無限遠点の1つだとしておきます。 その方が分かりやすいからです。
ふつう超球面 を半径1の球だとします。 そして、無限遠点
を半径1の球だとします。 そして、無限遠点 がくっついていますけれども、有限の大きさのものだとします。 それは、無限遠点をかならずしも無限に遠いところの点と考える必要がないからです。 円板モデルと似た考えです。
がくっついていますけれども、有限の大きさのものだとします。 それは、無限遠点をかならずしも無限に遠いところの点と考える必要がないからです。 円板モデルと似た考えです。
また、 はコンパクトではないが、
はコンパクトではないが、 はコンパクトであるといったりします。 コンパクトとは何か、といまは問わないでください。 このように表現するものだとしておきましよう。
はコンパクトであるといったりします。 コンパクトとは何か、といまは問わないでください。 このように表現するものだとしておきましよう。
超球面 も3次元だというのです。“面”とよんでいるのに。 それは、4次元ユークリッド空間の中で見れば、面と考えられるからです。
も3次元だというのです。“面”とよんでいるのに。 それは、4次元ユークリッド空間の中で見れば、面と考えられるからです。
この数学方言は、こうです。
円周を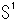 と表わし、球面を
と表わし、球面を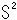 と表します。 それに連れて、超球面を
と表します。 それに連れて、超球面を と表します。 つまり、“球面”というものがあって、一つずつ次元を上げていっているわけです。
と表します。 つまり、“球面”というものがあって、一つずつ次元を上げていっているわけです。
そして、
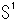 は、2次元ユークリッド空間
は、2次元ユークリッド空間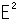 におけるもの。
におけるもの。
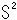 は、3次元ユークリッド空間
は、3次元ユークリッド空間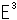 におけるもの。
におけるもの。
 は、4次元ユークリッド空間
は、4次元ユークリッド空間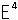 におけるもの。
におけるもの。
と考えます。
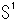 ,
, 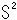 ,
,  ,,, をそれぞれ 1-球面、2-球面、3-球面、、、とよぶこともあります。 つまり、いずれも面であって、次元が違うだけだとみているわけです。 人によっては、超球面
,,, をそれぞれ 1-球面、2-球面、3-球面、、、とよぶこともあります。 つまり、いずれも面であって、次元が違うだけだとみているわけです。 人によっては、超球面 のことを単に「エスサン」とよんでいます。
のことを単に「エスサン」とよんでいます。
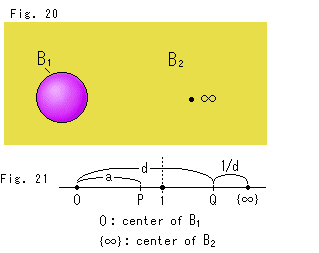 Fig. 20をご覧ください。
Fig. 20をご覧ください。
超球面 を捉える、もう一つの考えがあります。 こんどは2つの球体
を捉える、もう一つの考えがあります。 こんどは2つの球体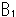 と
と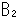 を使って超球面
を使って超球面 を得ます。
を得ます。
球体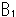 は、内部の詰まった半径1の球体です。 球体
は、内部の詰まった半径1の球体です。 球体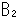 は、球体
は、球体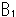 の外側の黄色く無限に広げられたところで、そこには余分な点
の外側の黄色く無限に広げられたところで、そこには余分な点 も含まれています。 球体
も含まれています。 球体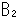 の中心は余分な点
の中心は余分な点 です。 このことは、2つの球体
です。 このことは、2つの球体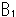 ,
,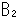 が、たがいに反転に似た関係にあるというわけです。
が、たがいに反転に似た関係にあるというわけです。
Fig. 21をご覧ください。
距離の測り方はこうです。 球体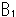 の中心は原点Oで、球体
の中心は原点Oで、球体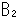 の中心は余分な点
の中心は余分な点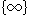 です。 半径は両方とも1にとります。 そうしておいて、球体
です。 半径は両方とも1にとります。 そうしておいて、球体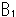 の中心Oから1以内(
の中心Oから1以内(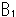 側)の点Pまでの距離は、ふつうの距離aとします。 球体
側)の点Pまでの距離は、ふつうの距離aとします。 球体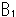 の中心Oから1以上(
の中心Oから1以上(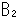 側)の点Qまでの距離は、球体
側)の点Qまでの距離は、球体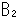 の中心
の中心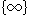 の距離を1/dとしたところのdとします。 こう約束しておくと、余分な点
の距離を1/dとしたところのdとします。 こう約束しておくと、余分な点 へは絶対にたどり着けないことになります。
へは絶対にたどり着けないことになります。
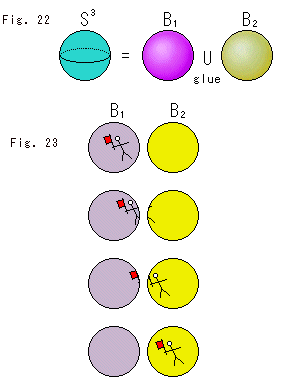
Fig. 22をご覧ください。
2つの球体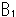 と
と の面と面を貼り合せると、超球面
の面と面を貼り合せると、超球面 ができます。 むろん、抽象的にです。 貼り合せ(glue)の記号は、和集合の記号Uと同じですが、それは球体を点の集合として考えているからです。
ができます。 むろん、抽象的にです。 貼り合せ(glue)の記号は、和集合の記号Uと同じですが、それは球体を点の集合として考えているからです。
Fig.23をご覧ください。
超球面 の中での様子です。 2つの球体
の中での様子です。 2つの球体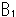 ,
,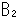 は、面と面が貼り合せてあると想います。 旗をもった人が
は、面と面が貼り合せてあると想います。 旗をもった人が の表面にくると、
の表面にくると、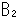 の表面に現れます。 そして、彼は
の表面に現れます。 そして、彼は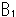 と
と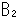 の中、つまり超球面
の中、つまり超球面 の中を自由に行き交うことができます。 しかし彼は、あの余分な点
の中を自由に行き交うことができます。 しかし彼は、あの余分な点 のところへも行けるのでしようか。 Fig.21の話しでは行けないことになっていますが、、、。
のところへも行けるのでしようか。 Fig.21の話しでは行けないことになっていますが、、、。
超球面 そのものは、どこにあっても(トポロジーの意味での)3次元です。 しかし、超球面は4次元ユークリッド空間
そのものは、どこにあっても(トポロジーの意味での)3次元です。 しかし、超球面は4次元ユークリッド空間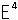 での曲面ですので、そのままでは見えません。 そこで、3次元にいながら空想力を動員して、抽象的にということでやったわけです。“抽象的に”というのは、なんと便利なことでしょう! しかし、無理強引な空想のようにも思えますね。
での曲面ですので、そのままでは見えません。 そこで、3次元にいながら空想力を動員して、抽象的にということでやったわけです。“抽象的に”というのは、なんと便利なことでしょう! しかし、無理強引な空想のようにも思えますね。
空想を補完するために、物語をいれます。
2次元の世界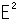 だけに住んでいる人たちがいます。 そこでは、すべてのものに(
だけに住んでいる人たちがいます。 そこでは、すべてのものに(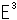 における)「上下」がありません。 彼らには、3次元の世界
における)「上下」がありません。 彼らには、3次元の世界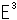 の実体験がまったくありません。 しかし、3次元なる世界
の実体験がまったくありません。 しかし、3次元なる世界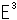 があって、そこに球面
があって、そこに球面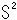 (ふつうの球面)というものがあることを知識として知っています。 それは、彼らの説明によると、こんなふうです。
(ふつうの球面)というものがあることを知識として知っています。 それは、彼らの説明によると、こんなふうです。
***** [空想物語] *****
我われが見ることのできない3次元の世界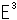 には、前後左右の他に「上下」という方向があるのです。 「上下」がどちらの方向かと問われても、我われの世界
には、前後左右の他に「上下」という方向があるのです。 「上下」がどちらの方向かと問われても、我われの世界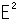 には、そんなものはないのですから、答えられません。 3次元の世界
には、そんなものはないのですから、答えられません。 3次元の世界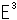 へ行くことができれば、すぐに示せますけれども、そこへ実際に行くことは不可能です。 ですから、球面
へ行くことができれば、すぐに示せますけれども、そこへ実際に行くことは不可能です。 ですから、球面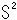 の存在を認めるには、そうとうな想像力が必要です。
の存在を認めるには、そうとうな想像力が必要です。
 まず、同じ大きさの円板(内部の詰まった円)
まず、同じ大きさの円板(内部の詰まった円)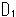 ,
,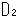 の2枚を用意します。 円板
の2枚を用意します。 円板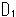 と円板
と円板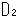 を3次元の世界の住人のように重ねるということができないので、やむなく円周と円周をそろえて貼り合わせます。 といっても、2次元の世界にいる我われには円周と円周の1点だけならつき合わせることができますが、円周全体と円周全体を貼り合わせることはできません。 しかし、物理的に不可能であっても、空想で抽象的におこなうことならできます。 ともかく、そのようにして、
を3次元の世界の住人のように重ねるということができないので、やむなく円周と円周をそろえて貼り合わせます。 といっても、2次元の世界にいる我われには円周と円周の1点だけならつき合わせることができますが、円周全体と円周全体を貼り合わせることはできません。 しかし、物理的に不可能であっても、空想で抽象的におこなうことならできます。 ともかく、そのようにして、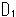 は「下」へ、
は「下」へ、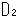 は「上」へ曲がっていると思ってください。 曲り具合は、円板の縁と同様です。 こうして想像されるものが、球面
は「上」へ曲がっていると思ってください。 曲り具合は、円板の縁と同様です。 こうして想像されるものが、球面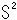 といわれているものです。 我われの2次元世界で内部の詰まっていた円が3次元の世界では、球面というもの一種の円になっていて、その中は空っぽです。“中”というのは、3次元の世界のことですが、我われの円におけるものと似た意味です。
といわれているものです。 我われの2次元世界で内部の詰まっていた円が3次元の世界では、球面というもの一種の円になっていて、その中は空っぽです。“中”というのは、3次元の世界のことですが、我われの円におけるものと似た意味です。
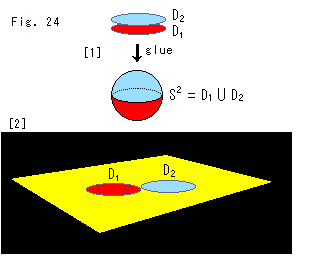
上のFig. 24をご覧ください。
[1]: 3次元の世界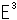 にいる人が描いたものです。 その人は、円板
にいる人が描いたものです。 その人は、円板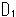 を下へ凹ませ、円板
を下へ凹ませ、円板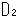 をを上へ凹ませて、円板の縁を貼り合せれば球面ができることを知っています。 そして、2次元の世界
をを上へ凹ませて、円板の縁を貼り合せれば球面ができることを知っています。 そして、2次元の世界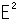 の人たちは、こう想像したのだろうと思いました。 しかし、それは誤っているようです。
の人たちは、こう想像したのだろうと思いました。 しかし、それは誤っているようです。
[2]: 2次元の世界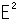 の住人は、この[2]のように2つの円板を並べて、ただただ空想したにちがいありません。 なぜなら、3次元の世界
の住人は、この[2]のように2つの円板を並べて、ただただ空想したにちがいありません。 なぜなら、3次元の世界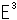 におけるどんななことも具体的にはイメージできないからです。
におけるどんななことも具体的にはイメージできないからです。
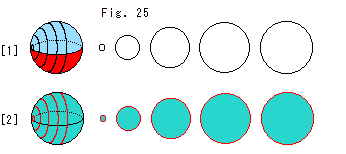 Fig. 25をご覧ください。
Fig. 25をご覧ください。
[1]: 2次元の世界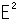 の住人も、球面
の住人も、球面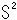 を、このようにスライスすれば見ることができます。
を、このようにスライスすれば見ることができます。
[2]: 私たちも、超球面 を、このようにスライスすれば見ることができます。
を、このようにスライスすれば見ることができます。
でも、スライスするには貼り合わされた結果が分かっていなければなりません。 それを知らずして、このスライスされたものだけを見て、貼り合わされている状態を推測することは容易ではありません。 つまるところ、強力な空想が必要だということになります。
ところで、ある人は、「超球面 は、
は、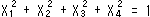 とも表せる。 これで3次元だ。」というのです。 こんなもので超球面
とも表せる。 これで3次元だ。」というのです。 こんなもので超球面 をイメージすることは至難ですね。 また、2つの中身の詰まったドーナツを貼り合わせて、超球面をつくる方法もあるそうです。 しかし、超球面そのものを追うことは目的ではありませんので、これくらいにしておきます。
をイメージすることは至難ですね。 また、2つの中身の詰まったドーナツを貼り合わせて、超球面をつくる方法もあるそうです。 しかし、超球面そのものを追うことは目的ではありませんので、これくらいにしておきます。
私たちの話しの中では、サーストンが超球面という言葉をつかっている場面は出てきません。 双曲正八角形の場面もありません。 しかし、これらの考え方は役立ちます。
超球面 をいろいろな方法で視覚化した美しい絵が、Webにたくさんあります。
をいろいろな方法で視覚化した美しい絵が、Webにたくさんあります。
Web1,
Web2,
Web3,
Web4,
Optiverse,
Outside In
(最後のOutside Inでは、MPEG movie of everting sphere をクリックすれば見れます。 ビデオです。)
それでは、これから8字ノットを見に行きましよう。
[前章] [次章] [目次]
 Fig.1をご覧ください。
Fig.1をご覧ください。
 Fig.6をご覧ください。
Fig.6をご覧ください。 Fig.8をご覧ください。
Fig.8をご覧ください。 抽象的な貼り合わせの結果は、頂点が1つ、辺が3つ、面が3つの奇妙な立体になります。
抽象的な貼り合わせの結果は、頂点が1つ、辺が3つ、面が3つの奇妙な立体になります。
 Fig.10をご覧ください。
Fig.10をご覧ください。 八角形について、すこし見ていきます。
八角形について、すこし見ていきます。



 Fig.17をご覧ください。
Fig.17をご覧ください。 Fig.18をご覧ください。
Fig.18をご覧ください。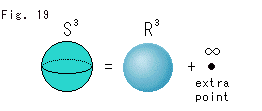 Fig.19をご覧ください。
Fig.19をご覧ください。 Fig. 20をご覧ください。
Fig. 20をご覧ください。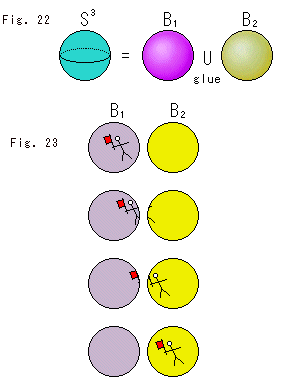
 まず、同じ大きさの円板(内部の詰まった円)
まず、同じ大きさの円板(内部の詰まった円) Fig. 25をご覧ください。
Fig. 25をご覧ください。