第４部 ８字ノット
Ch.52 ８字ノット (3) 
いよいよ８字ノットの話しに入ります。 といっても８字ノットそのものではなくして、その抜け殻である補空間(complement)というのが主題です。 補空間を扱う一番簡単なものが８字ノットだといわれています。
ノットの補空間とは、ノットがおかれている空間からノットを取り除いた残りの空間です。 鋳型のようなものですが、形の定まったものではありません。 数学的には、全体集合(空間)から部分集合(ノット)を抜き去った補集合だと表現されます。
下のFig.1は、これを観念的に描いたものです。 そして、その補空間が双曲的だといわれているのです。 本当でしょうか？
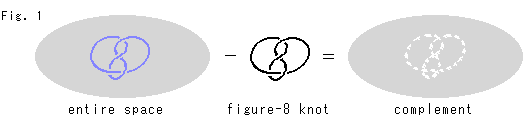
1978年、サーストンによって、ほとんどのノットの補空間が双曲的であることが発見されました。（双曲的でないのは、トーラスノットとかサテライトノットとよばれるものだけです｡） 彼は、それによって、1982年にフィールズ賞(ノーベル賞の数学版，４年に１度)を受けました。 その授賞理由に、なんと「革命的なことをした」と書いてあるではありませんか！（８字ノットが双曲的であることの最初の発見者はライリー(1974))
いったい、それはどんなことでしょうか？ ８字ノットで、サーストンの幾何化を見てみましょう。
｢８字ノットは、難しいですよ」と、私が訪ねたおおかたの数学者はいいました。 しかも、会う人ごとに説明がちがっていました。 それでもひるまずに、無鉄砲に筆をとっていきます。（世界初の俗本！）
話しは、2つの理想正四面体の面と面を抽象的に貼り合わせたものが、８字ノットの補空間だということです。 そして私たちは、その補空間をこの目で見ようと挑みます。
サーストンは、
特定のノットの補空間は、2つの四面体の特種な和集合として表わされる
（the complement of a particular knot can also be expressed as the union of two tetrahedra in a particular way.）
といっています。 これを式で表すと、
となります。
この式(1)の等号は、両辺が位相同型であることを示すもので、記号“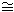
”の代用です。 左辺のマイナス“−”は、ふつうの引き算ではなくて、空間
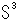からノットKを取り去ることです。
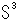を前章で超球面とよびましたが、
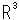に無限遠点を1つ加えた
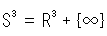であるとしておきます。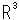は、ユークリッド空間
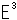が無限遠点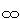
を含まない空間であることを明示したものです。 つまり、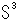は、日常の常識でのふつうの空間と考えてよいのです。 それで、これからは空間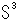とか、ただ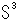と書くことにします。 無限遠点を1つ加えるというと、射影平面のように聞こえますが、そうではありません。 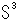は、ふつうに向きのある空間です。
「補空間は･･･として表わされる」といっているのは、補空間 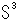- K を、それと位相同型だが別のもの T U T' - V に変えることができるということです。 同じことを、よく「補空間を2つの四面体に分解する」と表現されることがあります。
四面体T,T'は内部を含むものです。 内部を含むというのは、そこに何かを置いたり設定したりできることです。 内部を含むことを「中身の詰まった」ともいいますが、物理的なものが詰め込まれているわけではありません。
頂点Vは８字ノットが化身してなる1点です。 どんな化身かは、おいおいわかってきます。
式(1)の右辺は、左辺から演算で導き出せるものではありません。 いわば、話しによって左辺に結び付けられるものです。 お話しが証明になっているといわれています。
私たちが使う用語と記号を定めておきます。
式(1)の左辺 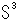- K を原始補空間とよびます。
四面体T,T'が原始補空間を二分して抱えている補空間を、T補空間と名付けて、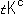
と表わします。
式(1)の右辺 T U T' - V は、いわば作業工程にすぎません。 そこで、貼り合せた結果としてできたものをマークで
と表わすことにします。 (こんなマークを使うわけは、後でうなづけるます｡)
８字ノットをノットKと略記したり、その補空間を単に補空間とよぶこともあります。
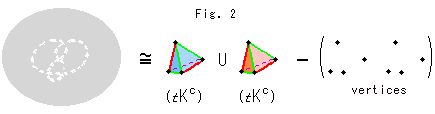
下のFig.2は式(1)をイラストしたもので、黒いスポットは切り取る頂点(vertices)です。
[前章] [次章] [目次]