第4部 8字ノット
Ch.53 8字ノット (4) 
8字ノットを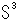 の中に置きます。 これにフィルムF,F'を張って、T補空間
の中に置きます。 これにフィルムF,F'を張って、T補空間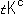 を含んだ2つの四面体T,T'を得ます。
を含んだ2つの四面体T,T'を得ます。
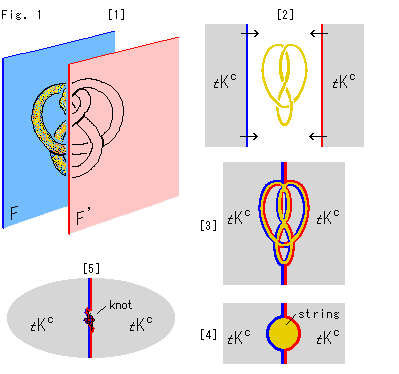 Fig.1をご覧ください。
Fig.1をご覧ください。
[1]: 2枚のフィルムF(空色)とF'(ピンク)を使います。 これらは仮想的なもので、実体はありません。 フィルムF,F'でノットKを挟んで密着させます。 いわば、ノットKを真空パックにするのです。 ただし、紐が立体交差しているところでは、そのように隔たりが保たれていて、その間にフィルムが入っていなければなりません。
[2]: フィルムF,F'は、それぞれの側のT補空間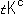 (灰色)を担います。 フィルムの表裏は、ノットKの側を表、T補空間
(灰色)を担います。 フィルムの表裏は、ノットKの側を表、T補空間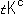 の側を裏とします。
の側を裏とします。
[3]: フィルムF,F'が、ノットKとその原始補空間の境界に割り入って、T補空間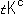 を接着したと思ってもよいでしょう。 図は観念的に描いたものです。
を接着したと思ってもよいでしょう。 図は観念的に描いたものです。
[4]: フィルムF,F'が張られたノットKの紐(string)の断面です。 どんなところでも、こうなっています。
[5]: フィルムF,F'が原始補空間を二分しているイメージです。 ノットKは、2つのT補空間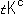 で挟まれています。
で挟まれています。
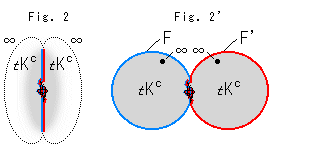
Fig.2のように、フィルムF,F'は無限遠まで延びて有限にもどってくるので、球状になっていると考えられます。
Fig.2'は、その球の断面を示すものです。 ただし、F,F'は、絵では左右に分かれていますが、(ノットKを挟んで)全面にべったり密着していると思って見てください。 フィルムF,F'が、それぞれのT補空間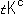 を抱えている様子です。 無限遠点
を抱えている様子です。 無限遠点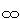 はどちらの側にあるとはいえませんが、1つのものを左右で共有しているといてもよいでしよう。
はどちらの側にあるとはいえませんが、1つのものを左右で共有しているといてもよいでしよう。
以下、小まめに読むのが面倒なら、粗雑にすませてFig.16へ飛んでもかまいません。
 上のFig.3をご覧ください。
上のFig.3をご覧ください。
T補空間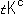 の入った四面体をつくるには、フィルムF,F'のそれぞれの面を四面体の面にしなければなりません。 フィルムのどこがどう面になるのでしようか。 写真は、そのおおよそを捉えるために、針金でつくったノットKを石けん水(シャンプー)に漬けて引き上げてみたものです。
の入った四面体をつくるには、フィルムF,F'のそれぞれの面を四面体の面にしなければなりません。 フィルムのどこがどう面になるのでしようか。 写真は、そのおおよそを捉えるために、針金でつくったノットKを石けん水(シャンプー)に漬けて引き上げてみたものです。
[1]: 赤い矢印で指している白い線に見えているのは、石けん膜どうしが交差しているところです。 泡が付いたり、膜面の石けん水が部分的に動いて渦になっていますが、無視してください。
[2]と[3]: [1]と同様に、石けん膜のある個所を針金が別の個所の石けん膜を着けて貫通しています。 針金が立体交差すると、そうなりいます。
表裏を見分けたいのですが、石けん膜は透明なので、とても困難です。
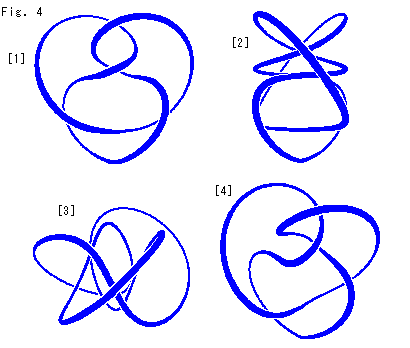 Fig.4をご覧ください。
Fig.4をご覧ください。
フィルムを張る前のノットKの形をよく観察してみましよう。 図は、パソコンに3次元での計算をさせて描いたものです。 計算といっても、ノットKとしての定まった形はありませんので、適当にアレンジしています。
[1]: ノットKの標準的な絵です。 この形を変えないで、動かしていきます。 紐の太さは遠近を表現しています。
[2]: [1]を垂直な中心軸のまわりに回転して横から見たものです。 重なって見えないところが出ないように、真横からすこしずらせています。
[3]: [1]を水平な中心軸のまわりに回転して上から見たものです。 こうなると、[1]の絵が頭にあっても、どこがどうなのか見ずらいですね。 見えないところがないように、これも真上からすこしずらせています。
[4]: [1]を勝手な向きにしたものです。 これも直ぐには、どこがどうなのか分かりませね。
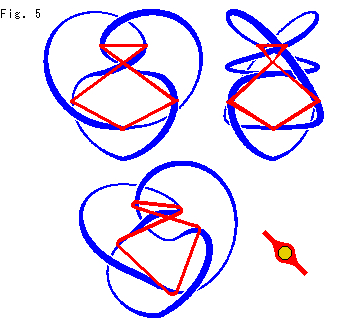 Fig.5をご覧ください。
Fig.5をご覧ください。
赤い線は、実際の石けん膜を観察して、膜と膜が交差しているところをノットKの絵の上に手で書き入れたものです。 右下に描いてあるのは、紐のところを通るこの交線が2つに別れて密着しながら迂回していく様子の断面です。 図では交線を真直ぐに描いていますが、本当はFig.3で見たように直線ではありません。 中央のXになっているところでは、4つの面が、たがいにある角度で集まって、1点に繋がっています。 これは、ノットを動かしたり、少々変形しても変わりません。 この交線のどの部分が、石けん膜のどの面とどの面の交わりといえばよいのでしようか。 すこし向きを変えて見ると、はじめに見た面ではなく、別の面と面が交わっているように見えます。
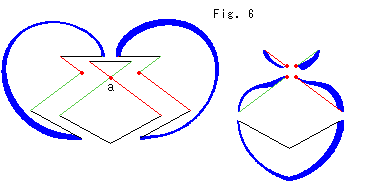
Fig.6をご覧ください。
実際の石けん膜を見ながら、その交線に沿って、Fig.5の左上の図を切ってみました。 見やすくするために、交線を色分けしています。 赤いスポットは、面が集まって1点でつながるところです。 赤いスポットaの上の三角形も下の四角形も1つの面です。 中空になったところはありません。 石けん膜はどこも一重です。 切り出した面は、全部で9枚にもなります。
こうしてみても、石けん膜の表裏を定めるには、どうすればよいのでしようか。 あるところを表ときめて辿っていくと、まるでメビウスの帯のような具合になってしまいます。 真空パックで考えれば、そんなことは絶対にないはずです。
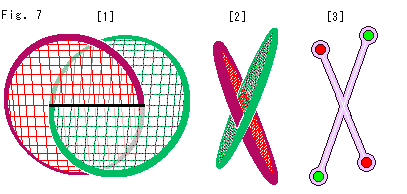
Fig.7をご覧ください。
針金のノットKに張られた石けん膜は絡んでいますので、単純なもので調べてみます。
[1]: かみ合っている2つの輪を石けん水に漬けて引き上げた状態です。 見やすいように石けん膜をあみ目で描いています。 黒い太い線が石けん膜の交線です。 石けん膜は、それぞれの輪に他と無関係に張られています。 2つの輪にまたがった石けん膜は生じません。
[2]: 横の方から[1]を見たもので、X状になっています。
[3]: X状になっているところでの石けん膜の断面です。 この場合、どの面を表と裏に選ぶかは、まったく自由です。
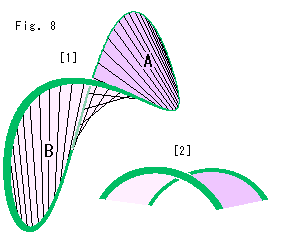
Fig.8をご覧ください。
[1]: ねじれた輪に石けん膜を張ったものです。 石けん膜はすなおに捻れた面になるだけです。 ノットKでは、Aのところが曲げられてBに噛みついたりしているので、ややこしいのです。 ですから、この素直にねじれた輪で考えることをもとにするのがよいと思えます。
[2]: こころみに、Fig.7の2つの輪の一部を同じ色にして、輪と輪の間を着色してみました。 すると、ねじれた面になります。 これもノットKを観察するときの混乱のタネのひとつです。
ノットKの紐が空間的に入りくんでいる様子や、石けん膜どうしの交わりのおおよそは、これで分かりました。 しかし、フィルムがどこにどのように張られいくのかを見て取ることは、容易ではありません。 そこで、フランシスの「トポロジーの絵本」を参考にしました。 以下は私たちなりに解釈したものです。 解釈といっても、何のためにそんなことをするのか解せないところがありますし、無意識に勝手な推測をしてしまっているかも知れません。 それでも、まずは見てみましよう。
Fig.9をご覧ください。
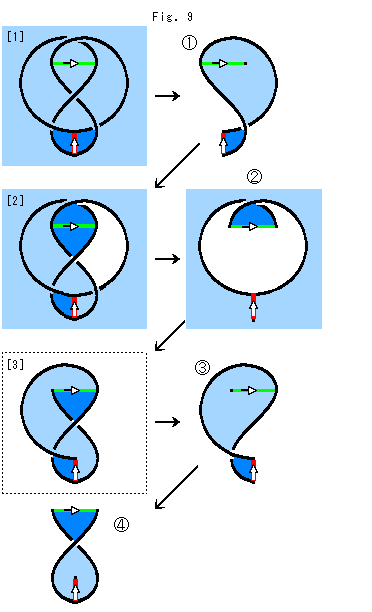
フィルムを4つに分割して四面体の4つの面を得ます。 まず、その分割です。
[1]: うすい青色のところが表面で、こい青色のところが裏面です。 フィルムは折れ曲がったり捩れたりして重なっていますが、見えている面だけを着色しています。 緑と赤の線は分割線です。 分割線の位置は図のところに限られるわけではありませんが、一応こうとっておくことにします。 矢印は分割線の向きを表わしています。 まず赤い分割線で切って、 を抜き出します。緑色の分割線の右端に紐の1点がくっついています。
を抜き出します。緑色の分割線の右端に紐の1点がくっついています。
[2]:  を[1]から取り去った後です。 白抜きのところは、
を[1]から取り去った後です。 白抜きのところは、 にとった部分で、フィルムが一重だったところです。 そこには何も残っていません。
にとった部分で、フィルムが一重だったところです。 そこには何も残っていません。  で覆われていたところが現れています。 その上の方ではフィルムの裏側が見えており、一番下の右側では表側が見えています。 この状態から
で覆われていたところが現れています。 その上の方ではフィルムの裏側が見えており、一番下の右側では表側が見えています。 この状態から を抜き出します。 赤い分割線の下端には、紐の1点がくっついています。 この1点は、
を抜き出します。 赤い分割線の下端には、紐の1点がくっついています。 この1点は、 の下端と同じ点です。
の下端と同じ点です。
[3]:  と
と が取り去られた後です。 四角い点線は
が取り去られた後です。 四角い点線は の周囲の痕跡ですが、そこは無限に広がったところですから、実際には周囲というものはありません。
の周囲の痕跡ですが、そこは無限に広がったところですから、実際には周囲というものはありません。  を取り出します。 最後の残ったところが
を取り出します。 最後の残ったところが です。
です。
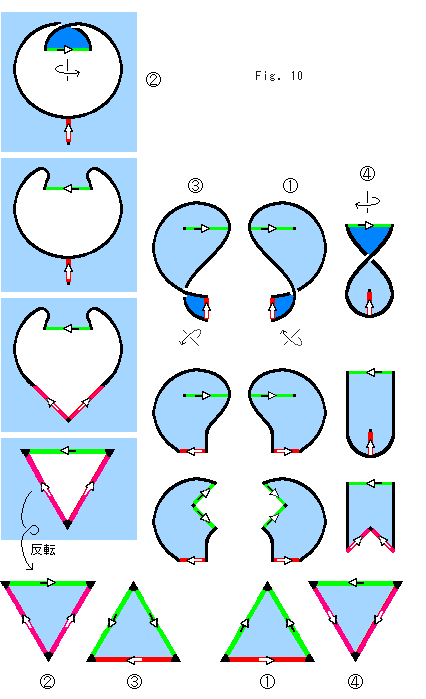
Fig.10をご覧ください。
フィルムFで、四面体Tの4つの面を作る工程です。 フィルムF'で四面体T'の4つの面を作る場合も同様です。
1. 上で得られた4つの面 ,
, ,
, ,
, の捻れをもどして、面の表をそろえます。
の捻れをもどして、面の表をそろえます。
2. 一端が紐とT字形につながっていない分割線を図のようにV字形に割きます。 V字形の頂点は紐の1点です。
3. 紐を一点に絞って三角形にします。  だけは、三角形をつくるために、その外側の面を反転で内側へもってきています。 それで、緑色の辺の向きが再び逆になっています。 ここでいう反転は、反転球の中心と半径をきっちりと定めておこなうようなものではありません。 点の位置をトポロジー的に移動するのです。 反転で平面図形は裏返りますが、面そのものが裏返ることはありません。
だけは、三角形をつくるために、その外側の面を反転で内側へもってきています。 それで、緑色の辺の向きが再び逆になっています。 ここでいう反転は、反転球の中心と半径をきっちりと定めておこなうようなものではありません。 点の位置をトポロジー的に移動するのです。 反転で平面図形は裏返りますが、面そのものが裏返ることはありません。
 上のFig.11をご覧ください。
上のFig.11をご覧ください。
真空パックは、その面が完全な一続きになっています。 石けん膜も同様です。 しかし、Fig.9やFig.10を見ると、フィルムと石けん膜は一致していません。 石けん膜はどこも一重ですが、フィルムでは重なった異なる面としているところがあります。 そこで、石けん膜と真空パックを比べてみます。 ノットKを実際に真空パックにしてみたわけではありませんが、十分推測できると思います。 真空パックでは、破ったり空気を入れたりしないで、外部から意図的に面の形を変えることができます。 (物理的に実行するには、ちょっと空気をいれるとよいでしよう。)
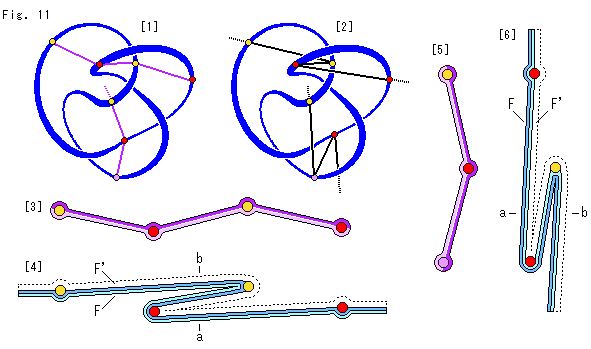
[1]: 石けん膜の断面を紫色の線で描いています。 上の方のは、紐の4つの部分にまたがっています。 下の方のは、紐の3つの部分を通る断面だけに注目しています。
[2]: 真空パックの断面を黒い線で描いています。 断面が紐の部分をめぐる順をわざと図のようにしています。 その両端を点線で描いてあるのは、真空パックではよぶんな広がりをとることができるからです。 上の方では、2つの黄色いスポットを通る断面が向こう側にあり、2つの赤いスポットを通る断面がこちら側にあります。 下の方でも、似たジグザグになっています。
[3]: [1]の上側の石けん膜の断面を[1]の上から見たものです。 [1]のこちら側の方をうすい色で、向こう側の方を濃い色にしています。
[4]: [2]の上側の真空パックの断面を[2]の上から見たものです。 着色してある方が[2]のこちら側で、フィルムFです。 点線は、[2]の向こう側にあるフィルムF'です。 フィルムFだけに注目します。 空色のうすい方が[2]のこちら側で、濃いほうが向こう側です。 a,bのところでこちら側(aの方)から順に見ると、はじめは表で、それをめくると裏が見え、まためくると表が見えます。 これはFig.9の話しと一致します。
[5]: [1]の下側の石けん膜の断面を[1]の右から見たものです。 図の左が[1]のこちら側で、右が向こう側になっています。
[6]: [2]の下側の真空パックの断面を[2]の右から見たものです。 a,bのところでこちら側(aの方)から順に見ると、はじめは裏で、それをめくると表が見え、まためくると裏が見えます。 これもFig.9の話しと一致します。
このように、真空パックで考えるのが適切だということがわかりました。 それなら、最初から真空パックで見ていけばよいと思われましようが、石けん膜での観察をしたからこそ、どのように成形した真空パックであればよいかが掴めたのです。
Fig.1のフィルムは、Fig.10の を別にすれば、この成形した真空パックと一致すると考えられます。 (成形を変えれば、トポロジーの別の話しになります。)
を別にすれば、この成形した真空パックと一致すると考えられます。 (成形を変えれば、トポロジーの別の話しになります。)
無限遠点を含んだところについて見ていきます。 無限遠点は、射影幾何の考えにならうと、どこにあるとしてもかまいません。 紐の上の1点だとしてもよいのです。 その場合、ノットKは無限に遠くまで伸びているとしてもよいわけで。 しかし、ここではノットKは有限で、その外側に無限遠点があるものを取り上げます。
ノットKは、2回ねじって自分自身と噛み合った輪です。 Fig.9の と
と の赤い分割線で切ったところをつなぎ戻すとそうなっているのがわかります。
の赤い分割線で切ったところをつなぎ戻すとそうなっているのがわかります。  と
と の緑色の分割線をつなぎ戻しても同様です。 このことを利用します。
の緑色の分割線をつなぎ戻しても同様です。 このことを利用します。
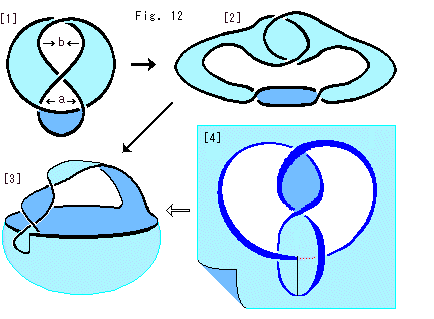 Fig.12をご覧ください。
Fig.12をご覧ください。
[1]: 注目する面にだけ色を塗ったものです。 白抜きのaのところを左右に広げます。 それにともなって、bのところが狭められます。
[2]: [1]のaのところを、うんと大きくしたものです。 これで、2回ねじれて噛み合っているのがはっきりと見てとれます。
[3]: [2]をさらに変形したものです。 ナベ形になりました。 これは、フランシスが描いて見せてくれたものです。 [2]から[3]への変形を順を追って見ていってもよいのですが、2回ねじれて噛みつくものだということで、このナベに直接変形できます。
[4]: この[4]からもナベ形が得られます。 2回ねじって自分自身に噛みついているのですから。 水色のところをフィルムFだとすると、濃い色のところはその裏側で、フィルムF'ということになります。 白抜きのところは、ナベのふちと柄(ノットK)の形に合った蓋に対応しています。 蓋は左右に分かれた2つではなく、捩じくれた1つのものです。
この[4]から[3]を見ると、ノットKがナベのねじれた柄と淵になり、ノットKの外側の広大無辺なところがナベの器になったのです。 後者には、反転という操作が入っています。 このようにして、一切を目で捉えることができました。
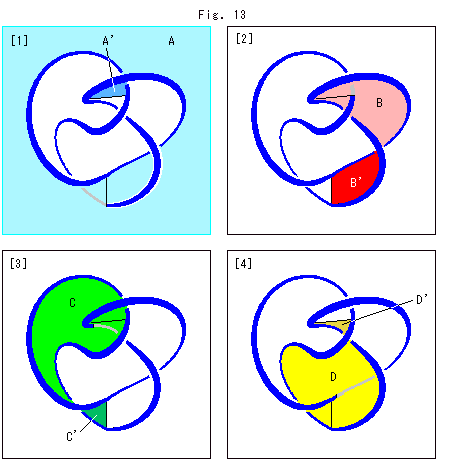 Fig.13をご覧ください。
Fig.13をご覧ください。
工程図のFig.10で、ノットKに張られたフィルムのどこが四面体をつくる三角形になるかを見ました。 フィルムとノットKとの関係がわかったので、その四面体の4つの三角形になるフィルム面を色分けして、個別に立体的に見てみます。
各面の記号を、ノットKの立体的な絡みと後の都合にあわせて、

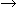 B
B

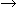 A
A

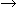 C
C

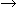 D
D
と変えています。 以後、三角形についても同様にA,B,C,Dで表わすことにします。
ダッシュを付けてあるのは裏側で、濃い色にしています。 黒い線は分割線ですが、[1]と[4]の下の方の分割線で面Aと面Dが分割されることはありません。 また、上の方の分割線で面Bと面Cが分割されることもありません。
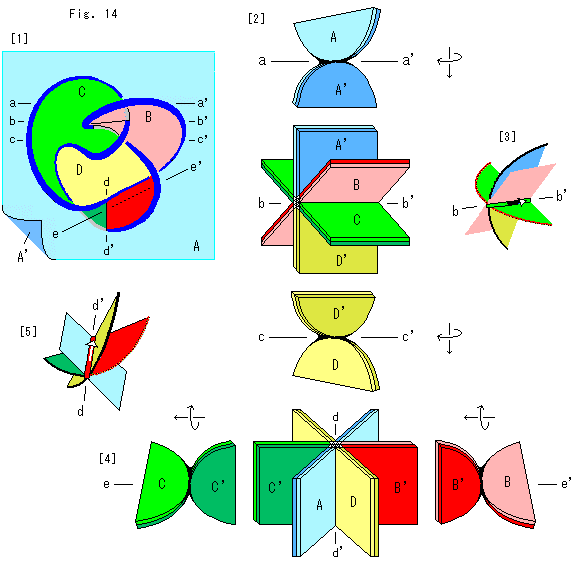
上のFig.14をご覧ください。
フィルムは一続きの面ですが、巧妙に絡んでいます。 四面体の4つの三角形となる面の、分割線のところの面と、その前後の捻れの様子を見てみます。 捻れの実際はゆるやかですが、極端に描いています。
[1]: Fig.13の4つの図を重ねて、Fig.9の[1]の状態にしています。 a-a'は、aからa'の方へ視線を向ける位置です。 他の小文字の記号も同様です。 b-b'とd-d'は、分割線を乗せた方向です。
[2]: 上から順にみていきます。
a-a'では、面Aが矢印のようにねじれて裏返っています。
b-b'は分割線のところに4つの面が集まっている様子です。 面A(A')と面D(D')が、ここで分割されます。
c-c'では、面Dが矢印のようにねじれています。 面A(A')と面D(D')を一続きにみると、同じ方向に2回ねじれているわけです。
d-d'は縦の分割線のところに4つの面が集まっている様子です。 面B(B')と面C(C')が、ここで分割されます。
[3]: b-b'のところの左の方の眺めです。
[4]: e-e'の右の方では面Bが、左の方では面Cが、それぞれ矢印の方向にねじれています。 面B(B')と面C(C')を一続きに見ると、ここでも同じ方向に2回ねじれています。
[5]: 分割線のあるd-d'のところを下の方から見たものです。
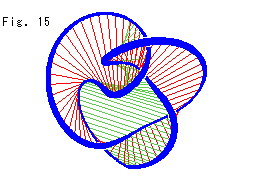 Fig.15は、フィルムを張った様子です。 緑色の線のところが、面A'と面Dで、赤い線のところが面Bと面Cです。 ノットKの外側は省いています。 実際に工作したものを手にとって見るのが一番よいのですが、写真にするとどうなっているのかよく分かりません。 それで、パソコンで描きました。 それでも、ちょっと見にくいですね。 できれば、皆さんも工作してみてください。
Fig.15は、フィルムを張った様子です。 緑色の線のところが、面A'と面Dで、赤い線のところが面Bと面Cです。 ノットKの外側は省いています。 実際に工作したものを手にとって見るのが一番よいのですが、写真にするとどうなっているのかよく分かりません。 それで、パソコンで描きました。 それでも、ちょっと見にくいですね。 できれば、皆さんも工作してみてください。
私たちのフィルムの紙細工も見てください。
Webにもいくつかの絵があります。
Knot Spanning Surfaces は、小さな三角形で面をブロック化したものです。
Soap Films on Knotsは、ちがった形のノットKにコンピュータによる石けん膜が張られています。
Soap Film - Minimal Surfacesは、ノットKとは関係のない一般の石けん膜です。
**************************************************
ノットKを挟んだフィルムF,F'の様子が、すっかりわかりました。 それでは、フィルムF,F'から四面体T,T'をつくることにしましよう。 これは簡単です。
 Fig.16をご覧ください。
Fig.16をご覧ください。
[1]: フィルムFから得た4つの三角形A,B,C,Dを辺(分割線)の色と向きが一致するようにつなぎ合わせたものです。 これ以外にも同じ条件で、いろいろに並べることができます。 黒いところは、分割線の端についていたノットK上の点です。 あとで、それは切り落とします。
[2]: [1]の表を外側にして四面体Tにしたものです。 三角形から四面体Tを直接つくってもかまいません。 フィルムFを4つに分割し捩れをもどしてつなぎ直すと、このように四面体ができるのです。
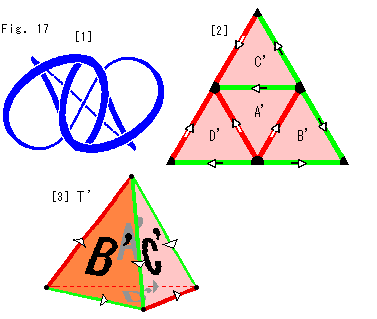 Fig.17をご覧ください。
Fig.17をご覧ください。
もう一つの四面体T'をつくります。 フィルムF'でFig.10の工程をふんでもよいのですが、フィルムFで得られたことを利用します。
[1]: 形を整えたノットKを真上から見たものです。 完全な点対称になっています。 ですから、張られるフィルムF'もフィルムFとたがいに点対称です。 そして、フィルムFの裏側がフィルムF'の表側ということになります。 そこで、三角形A,B,C,Dの裏側の記号A',B',C',D'をそのままフィルムF'から得られる三角形の(表側の)記号につかいます。 これらの三角形の裏側についてどうこうすることはもうありません。
[2]: フィルムF'の三角形を並べたものです。 それは、Fig.16の[1]を裏返したものと同じですが、担っているT補空間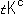 は、その裏側(向こう側)にあります。 三角形B'と三角形D'がFig.16の[1]とは逆の位置にあります。
は、その裏側(向こう側)にあります。 三角形B'と三角形D'がFig.16の[1]とは逆の位置にあります。
[3]: [2]からつくった四面体T'です。 四面体Tにならって、三角形B',C'をこちらに向けて描いたので、三角形A'と三角形D'がFig.16の[2]とは逆のところになっています。
これで2つの四面体T,T'が完成しまいた。 あとの都合のために、正四面体にしておきます。 それぞれの四面体の頂点を除いた表面と内部にT補空間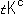 が入っています。
が入っています。
[前章] [次章] [目次]
 Fig.1をご覧ください。
Fig.1をご覧ください。

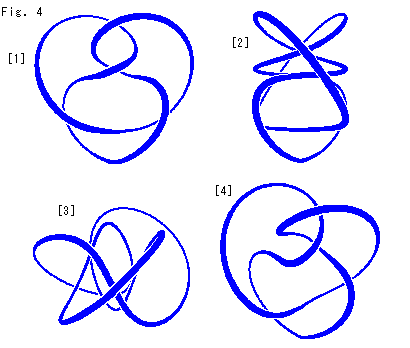 Fig.4をご覧ください。
Fig.4をご覧ください。 Fig.5をご覧ください。
Fig.5をご覧ください。
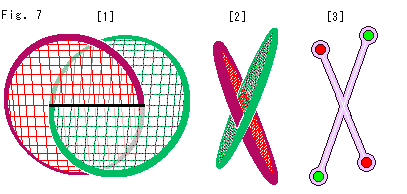




 Fig.12をご覧ください。
Fig.12をご覧ください。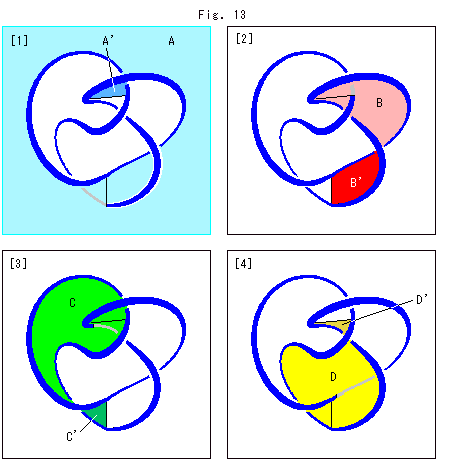 Fig.13をご覧ください。
Fig.13をご覧ください。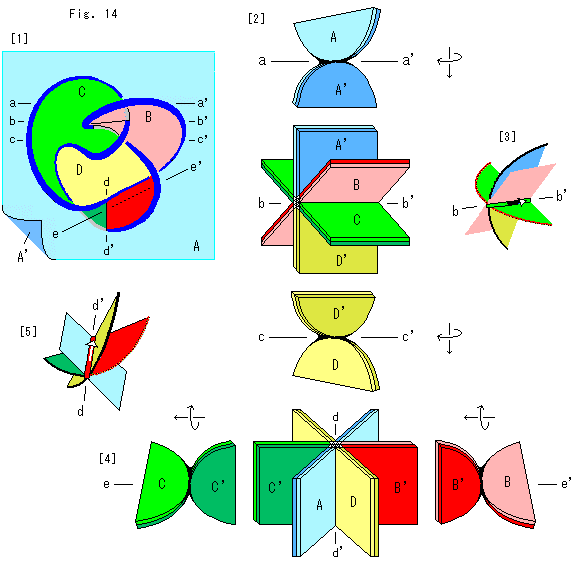
 Fig.15は、フィルムを張った様子です。 緑色の線のところが、面A'と面Dで、赤い線のところが面Bと面Cです。 ノットKの外側は省いています。 実際に工作したものを手にとって見るのが一番よいのですが、写真にするとどうなっているのかよく分かりません。 それで、パソコンで描きました。 それでも、ちょっと見にくいですね。 できれば、皆さんも工作してみてください。
Fig.15は、フィルムを張った様子です。 緑色の線のところが、面A'と面Dで、赤い線のところが面Bと面Cです。 ノットKの外側は省いています。 実際に工作したものを手にとって見るのが一番よいのですが、写真にするとどうなっているのかよく分かりません。 それで、パソコンで描きました。 それでも、ちょっと見にくいですね。 できれば、皆さんも工作してみてください。 Fig.16をご覧ください。
Fig.16をご覧ください。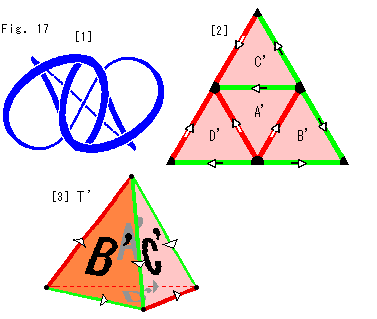 Fig.17をご覧ください。
Fig.17をご覧ください。