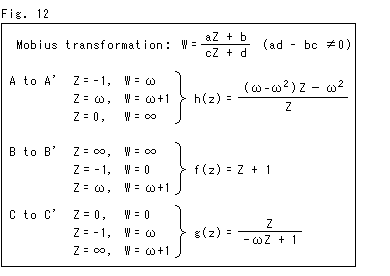第４部 ８字ノット
Ch.54 ８字ノット (5) 
2つの四面体T,T'を貼り合わせて、新しい補空間を得ます。 それは、双曲空間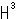
の中に見出されます。 いわゆる幾何化です。
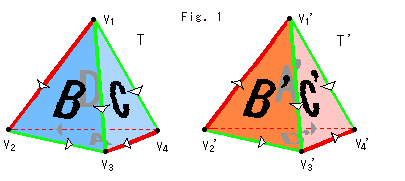貼り合わせは、フィルムF,F'が密着していたときの面と面が一致するように行います。 AとA'、BとB'、CとC'、DとD'をそれぞれ、辺の色と向きをそろえて、貼り合わせるのです。 むろん、四面体T,T'の外側と外側を貼り合わせるのです。 面のラベルA,B,,,やA',B',,,は面ではないのいで、どちらを向いてもかまいません。
Fig.1のように頂点に記号をいれておきます。
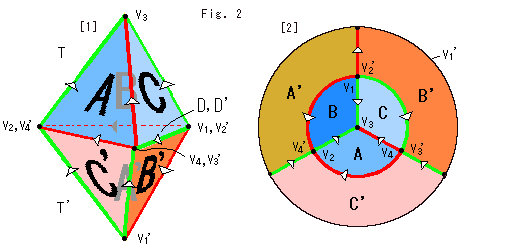Fig.2をご覧ください。
[1]: 面DとD'だけを貼り合わせたところです。
[2]: [1]を上から立体射影のようにしてパターン図にしてみたものです。 面Dと面D'は描かれていませんが、頂点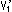
が外側の円になっていて、[1]で見られる頂点にまたがっています。
物理的に張り合わせできるのは、AとA'とか、BとB'などの一組の面しかできません。 しかし、心で想って抽象的に続行します。
この貼り合わせは抽象的なものですから、実行する空間のことは考えません。(SF小説のように4次元世界で貼り合わせると想ってはいけません。 なによりも、4次元の世界ではどんなノットもほどけてしまって、話しになりません｡)
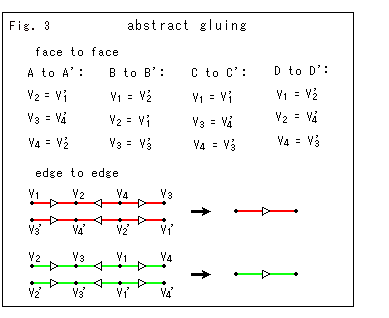
Fig.3の囲みは、抽象的張り合わせ(abstract gluing)のルールです。
いま、これにしたがって四面体T,T'の面と面(face to face)の張り合わせができたとします。 すると、面の数は当然4つになります。 ところが頂点は、同一視されて最後には1個の頂点V
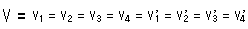になります。
また、辺は赤と緑の2つだけになります。
辺が2つになったのは、辺のもとは赤と緑の2本の分割線ですから当然です。 頂点のもとは1つのノットKですから、それが1つになったのも当然です。 そうだけれども、妙なぐわいですね。
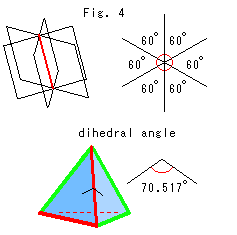
Fig.4をご覧ください。
ルール通りに張り合わせができるためには、6つの辺が重なって1つになるのですから、辺角(dihedral angle)は60
でなければなりません。 ところが、ふつうの正四面体の辺角は70.517です。 これでは隅を詰めることができません。
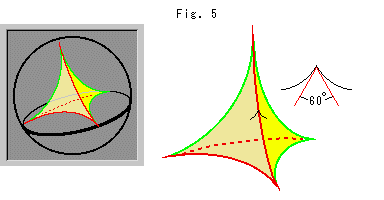Fig.5をご覧ください。
ここで登場するのが、双曲幾何の球体モデルです。 図はポアンカレのモデルで描いています。 正四面体の大きさについては、これまでに何もいっていません。 そこで、正四面体として頂点が無限遠へと伸びているものを選ぶことにします。 これは、ノットK上の1点を無限遠点にとったことになります。 それを双曲空間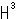(球体モデル)の中へそれを入れると、正四面体は理想正四面体になり、その辺角は自動的にちょうど60になります。
ただし、先に頂点を切り落としておかねばなりません。 理想正四面体には頂点はないからです。 それに、私たちが得ようとするのは補空間だけですから、ちょうど都合がよい。 内角45の双曲正八角形をつくったときのように、大きさを調節する必要はありません。
サーストンの式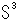 
- K = T U T' - V の右辺は「張り合わせて(T U T')、それから、1点となった頂点Vを取り去る」と読めます。 しかし、話しが合うようにするには、張り合わせをする前に頂点を除いておく必要があります。 右辺を書き直すとすれば、
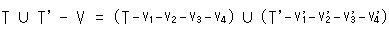
となります。 しかし、こんなふうに書かれていないのがふつうです。 私たちも、慣用にならった書き方にしたがうことにします。
ともかく、頂点のない2つの四面体T,T'を貼り合わせればよいのです。 ただし、それは双曲空間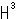といったような具体的な空間の中でおこなうのではなく、そんなものは考えないで、まったく抽象的にパッと想うのです。 四面体の外界のことは考えませんけれども、その内部には双曲的空間が維持されます。
そうして貼り合わせた結果は、
頂点がゼロ、辺が2つ、面が4つ
という奇怪なモノになります。
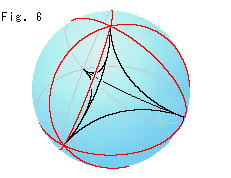
Fig.6をご覧ください。
理想正四面体の辺角が60であることは、3つの頂点を通る円が頂点のところで球体モデルの面を6等分していることからわかります。 もちろん、クラインの球体モデルでも同じです。 実は、理想四面体なら理想“正”四面体でなくても、隣り合う6つの辺角を合計すると360になります。 しかし、そのことには触れないでおきます。
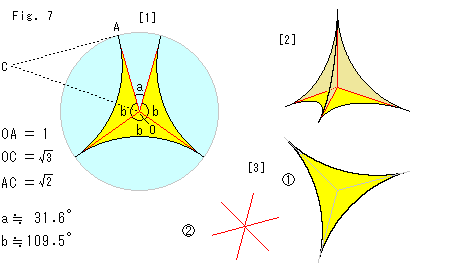Fig.7をご覧ください。
理想正四面体の辺角は、計算するかFig.6を見れば、60であることはわかります。 しかし、3-Dイメージを掴むのにかなりの思い入れをしなければなりません。 そこで、簡単な紙細工を紹介します。
[1]: 黄色く塗った形のものを3つつくります。 水色の円は半径1の作図用のものです。 角bは、理想正四面体の中心から2つの頂点を見た角です。 円弧は理想正四面体の稜線です。 左上の円弧では、中心がCのところにあって、三角形ACOは直角三角形です。
[2]: [1]のaのところを閉じたもの3つを、赤い線がそろうようにつないだものです。
[3]: 
は[2]を真上から見たもです。 
は、その稜線をなしている3つの円が理想正四面体の頂点で交わっているところです。 明らかに辺角は60です。
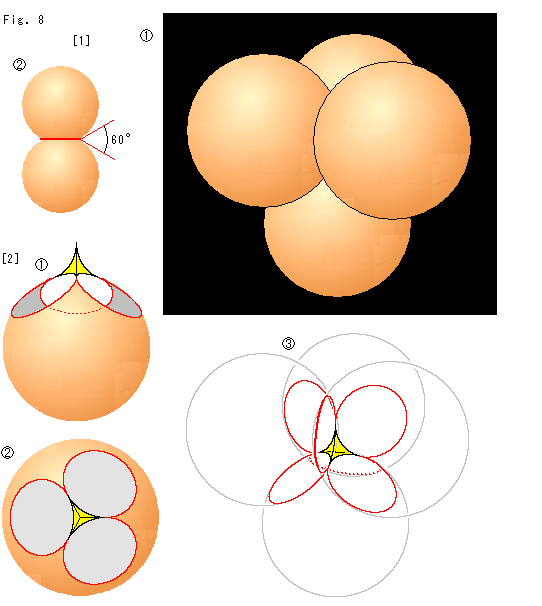
Fig.8をご覧ください。
理想正四面体の辺角が60だというのは、むろん辺のどこで測ってもそうだということです。 Fig.6から察しられますが、それを確かめておきます。
[1]: 理想正四面体の面は4つの球面でのように挟まれています。 その隣り合う2つだけをとって、球面と球面の交線を水平にして見ると、のように2つの球面が60をなして交わっています。 どの2つの球面もこうなっています。
[2]: 球面の1つに理想正四面体が乗っています。 は理想正四面体を真っ直ぐに立て、辺(稜線)の1つをこちらへ向けたところです。 その全体を真上から見ると、のようになっています。 
は、[1]の4つの理想正四面体を透視したものです。 赤い楕円は球面と球面の交線で、6つのそれぞれ交線の一部が理想正四面体の辺になっています。
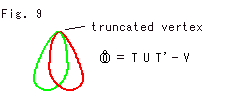
Fig.9をご覧ください。
頂点のない2つの四面体T,T'の面と面が張り合わされたモノ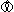
(= T U T' - V) を観念的に描いたものです。 赤と緑の2つの辺が、欠けた頂点(truncated vertex)のところで出会っています。 辺は曲げて描かれていますけれども、真直ぐだと想ってください。 面は描かれていませんが、4つあると想ってください。
それでも、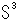からノットKを取り除いた補空間 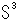- K に位相同形な新しい補空間 T U T' - V です。 古いものは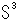にあり、新しいモノ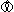は T U T' - V である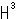だというわけです。
これで、幾何化ができました。 幾何化とは、ある空間を定まった幾何をもつものにする(幾何構造を与える)ことです。 幾何とは距離を保つものだとします。“保つ”というのは、物では形と大きさが定まっており、空間では物差し(計量)が一定だということです。
**************************************************
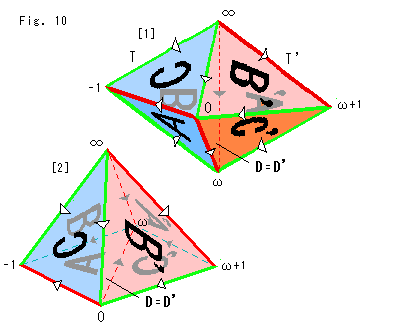
Fig.10をご覧ください。
貼り合せを、ちょっと数式にたよってみます。
[1]: 六面体を便宜的に横にしたものです。 上半空間H3+を利用するために、頂点(本当は無い)の位置を、複素数で表わしています。 六面体で面Dと面D'を張り合わせて同一視した頂点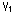
,
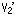を無限遠点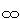
にとっています。
[2]: 面Aと面C'を底面として、[1]をピラミッド形に描いたものです。
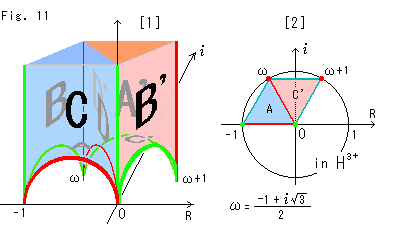
Fig.11をご覧ください。
[1]: Fig.10の[2]のピラミッドを上半空間H3+に置いたものです。 面Aと面C'は球面です。 面Bと面B'が向かい合っています。 物理的な矛盾が出ないのは、ここまでです。 図の上の方は、見やすくするために、途中で切っています。
[2]: [1]を真上から見たものです。 Rは実軸で、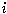
は虚軸です。 上半空間の床(R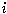平面)をふつうのガウス平面としてあつかいます。 ただし、距離や変換式がユークリッド的でないことはいうまでもありません。
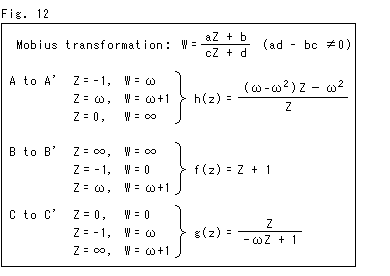
Fig.12の囲みは、貼り合わせの計算式(メビウス変換)です。
面Aを面A'に貼り合わせる変換式 h(z)は、
Zに面Aの頂点、Wに面A'の頂点を与えて、
メビウス変換の式をa,b,c,dについて解き、
得られたa,b,c,dの値をメビウス変換に代入する
と得られます。
f(z), g(z) についても同様です。
この式は、たしかに、すべての面の貼り合わせを表わしています。 同じ頂点 -1 が面Aではωに、面Bでは 0 に移ります。 また、同じ頂点 ω + 1 へ面Aの頂点 -1 からも面Bの頂点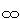からも移ってきます。 こういったことを素直に受け入れています。 Z → W での式ですが、W → Z で考えても同様です。 物理的に不可能でも、難なく処理できます。 数学的な矛盾は、どこにもありません！
しかし、この式は、いわば作業工程を表わしているだけで、ことばでの表現と差異はありません。 貼り合わせた結果については、何もいっていません。 驚いたことに、貼り合わせたモノ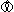を表わす数式はありません。 魔法のようなことを素直に受け入れる空想力でまかなうほかないことが分かりました。 (このFig.12については、後でまたふれます｡)
それにしても、いともあっさりと幾何化できましたね。 でも、なにか騙されている気がしませんか。 辺角60というところまではきっちりやっていますが、そのあとは一気に“抽象的に”ですまされています。 もうすこし当たってみましよう。
[前章] [次章] [目次]