第4部 8字ノット
Ch.55 8字ノット (6) 
幾何化といわれていることを行いましたが、その意味合いがはっきりしません。 それは、2つの四面体を抽象的に貼り合せたモノ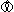 (= T U T' - V)が見えないからです。 どうにかして
(= T U T' - V)が見えないからです。 どうにかして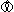 の姿を捉えましよう。
の姿を捉えましよう。
平面などで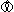 を切って、その切口を見ることができるとよいのですが、切るためには
を切って、その切口を見ることができるとよいのですが、切るためには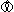 を具体的な座標(空間)の中に埋めねばなりません。 そんなことをすれば、トポロジーは維持されても、幾何構造が壊れてしまいます。 そこで、展開図で見ることを考えます。 サーストンがそれを示してくれていますので、なんとか辿ってみます。
を具体的な座標(空間)の中に埋めねばなりません。 そんなことをすれば、トポロジーは維持されても、幾何構造が壊れてしまいます。 そこで、展開図で見ることを考えます。 サーストンがそれを示してくれていますので、なんとか辿ってみます。
その手掛かりは、あの切り捨てた頂点にあるのです。 どういうことでしようか。
ノットKは、その補空間を得るために四面体T,T'の頂点に押し込められて、切り捨てられました。 いま何処でどう暮らしているのでしようか。
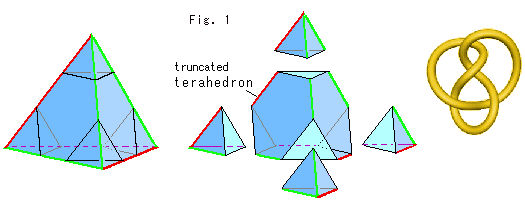 Fig.1をご覧ください。
Fig.1をご覧ください。
ノットの紐がついている四面体の頂点付近を大きく切ってみます。 そこは肥ったノットに対応します。 頂点付近を切り落とした四面体を切頭四面体(truncated tetrahedron)とよぶことがあります。
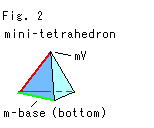 Fig.2をご覧ください。
Fig.2をご覧ください。
これからの話しのために、
切り落とした小さな四面体を --- ミニ四面体 (mini-tetrahedron)
ミニ四面体の底面を --- 底面mB (m-base)
底面mB上にはない頂点を --- 頂点mV
とよぶことにします。
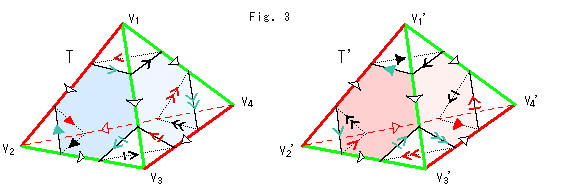
Fig.3をご覧ください。
四面体T,T'から切り出すミニ四面体の底面mBの辺に図のように矢印をつけます。 この矢印は、四面体T,T'の張り合わせルールに符合させます。
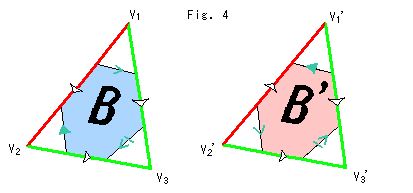 Fig.4をご覧ください。
Fig.4をご覧ください。
底面mBの辺の矢印を間違いなくつけるには、まず四面体T,T'のいずれか一方のミニ四面体の全部に矢印を付けます。 矢印はすべて異なるものにします。 もう一方の四面体のミニ四面体の矢印は、2つの四面体T,T'が張り合わされたときに底面mBの矢印が一致するようにつけます。 図はその例で、面Bと面B'におけるものです。
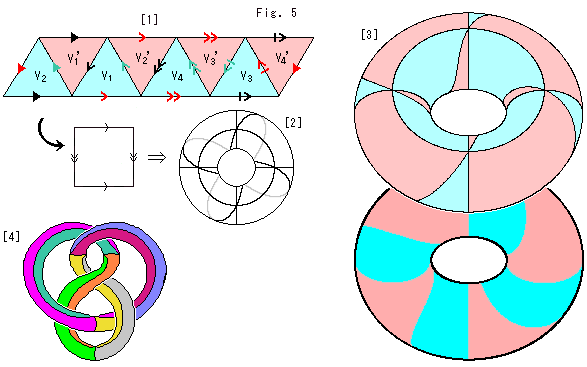 上のFig.5をご覧ください。
上のFig.5をご覧ください。
[1]: Fig.3の8つのミニ四面体の底面mBを矢印が一致するようにして並べます。 そして、その周囲の矢印を見ると、トーラスのあの矢印つき正方形と同じではありませんか! 位相同形です。
[2]: [1]をドーナツ形に描いたものです。 こうすると、底面mBの矢印のついた辺がすべて貼り合わせられます。
[3]: [2]のスケルトンは見にくいので、2つに切ったものです。 4か所で6つの三角形が頂点を共有して、60 x 6 = 360
x 6 = 360 が満たされています。
が満たされています。
[4]: 参考のために、太いノットKに8つの三角形を張ってみたものです。 このように張れはしますが、底面mBをつかうことはできません。 ノットKは、もとは8の字の形をしていたのですが、四面体T,T'の頂点になったいまは、そうではないからです。
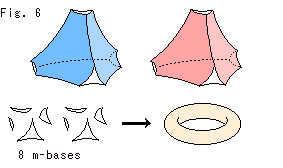
Fig.6をご覧ください。
Fig.5までの話しを一つにした絵です。 ポアンカレ球体モデルの理想四面体で描いていますが、もちろんクラインの球体でも同じことです。 2つの理想四面体の頂点を大きく切って得られる8つの底面mBがトーラスになるということです。 頂点を切り落とされた2つの理想四面体T,T'は貼り合わされていませんが、8つの底面mBがトーラスになるのは、その貼り合わせが行われた場合のものです。
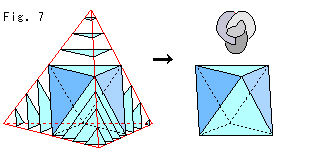 Fig.7をご覧ください。
Fig.7をご覧ください。
底面mBは貼り合わされた理想四面体をスライスしたものだとみると、あの見えないといっていたノットKの補空間の姿が現れたことになるではありませんか!
それも私たちに馴染みのあるトーラスです。 補空間としては、トーラスの面と面が積み重ねられたものになります。 2つの立方体を貼り合わせた3-トーラスの話しと似ています。 しかし、頂点のところからスライスをしていくと、途中で8つの底面mBが得られなくなります。 そこは、ノットKの紐が太くなって、紐と紐の隙間がなくなってしまうところです。
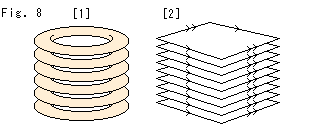
Fig.8をご覧ください。
[1]: まるで積み上げてある車のタイヤのようですね。 切り出すことのできるトーラスでノットKの補空間の一部をイラスト表現したものです。 本当は、隣り合ったトーラスの全面と全面が密着していなければなりません。
[2]: ドーナツではなく、矢印つき正方形のトーラスです。 これなら、面を全部くっつけることができます。
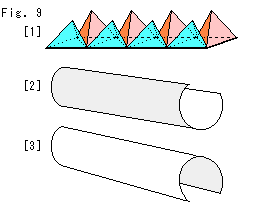
Fig.9をご覧ください。
[1]: 底面mBを並べたFig.5の[1]の上にミニ四面体を置いたものです。
[2]: 矢印つき長方形からドーナツ形のトーラスを得るには、始めに円筒をつくります。
[3]: 長方形を[2]とは逆に巻いて円筒をつくってもかまいません。 矢印つき長方形は裏返しても、まったく同じだからです。 しかし、長方形の上に物がある場合は、様子がちがってきます。
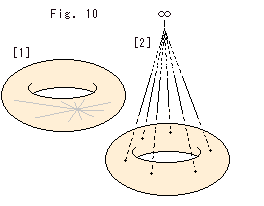 Fig.10をご覧ください。
Fig.10をご覧ください。
底面mBからなるトーラス上には、抽象的に貼り合わされた理想四面体の(欠けた1つだけの)頂点があると考えられます。
[1]: Fig.9の[2]によって作ったトーラスに、理想四面体が貼り合わされたときのミニ四面体を観念的に描き込んだものです。 頂点がトーラスの内部の1点に集められています。 これでは、その1点が無限遠にあることにはなりません。
[2]: Fig.9の[3]のようにしてトーラスをつくると、本質的には[1]と変わりませんが、ほどよい観念図になります。 集められた頂点が無限遠へ飛んでしまっている感じになっていますね。
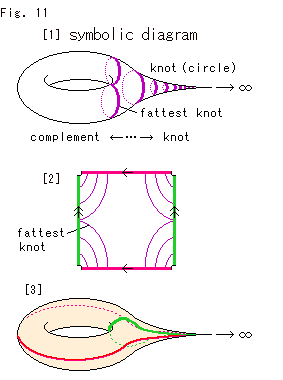
Fig.11をご覧ください。
[1]: シンボリックダイアグラム(象徴図, symbolic diadram)です。 ノットKを紫色のループで表わしています。 その一番左側のは、Fig.7にあるもっとも肥えた(fattest)ノットです。 そこから左はFig.7の八面体に相当します。 ノットKは、右へ行くほど小さくなり、無限の彼方では消滅しています。 この紫色のノットより左の方が補空間です。 この図はノットKのことをよく物語っています。 しかし、補空間の面が1つしか描かれていないので、空想で補わねばなりません。
[2]: [1]を表わす、四隅の欠けた正方形です。 一番内側の紫色の線がもっとも肥えたノットKです。
[3]: ノットKが[2]の四隅へ追いやられて切り捨てられたときのものをトーラスにしたものです。
Fig.7などでノットKの補空間の片鱗が見えました。 追って行きましよう。
[前章] [次章] [目次]

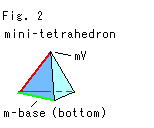 Fig.2をご覧ください。
Fig.2をご覧ください。
 Fig.4をご覧ください。
Fig.4をご覧ください。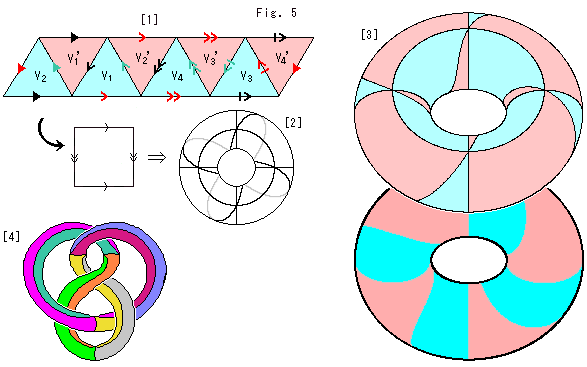

 Fig.7をご覧ください。
Fig.7をご覧ください。

 Fig.10をご覧ください。
Fig.10をご覧ください。