第4部 8字ノット
Ch.56 8字ノット (7) 
2つの理想四面体T,T'の頂点を切った切口からトーラスを得ました。 それは、四面体T,T'がまだ抽象的に貼り合わされていなくても可能でした。 そして、そのトーラスは矢印付きの三角形で十分認識することができました。
そこで、理想正四面体を球体モデル内に敷き詰めたものから考えていきます。
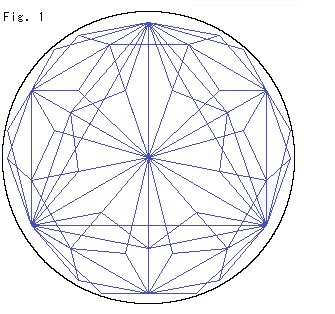
Fig.1をご覧ください。
クラインボール内に理想正四面体を積みます。 図は真中に1つおいて、その周囲に理想正四面体を3層だけならべたものです。 辺をスケルトンで描いているのですが、とても見にくいですね。
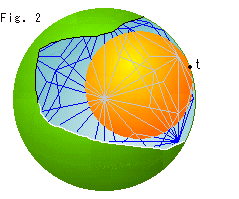
Fig.2をご覧ください。
クラインボールの殻を破って、中にあるホロスフィアを覗いたところです。 ホロスフィアは、理想正四面体がぎっしり詰まっている球体と点tで内接しています。
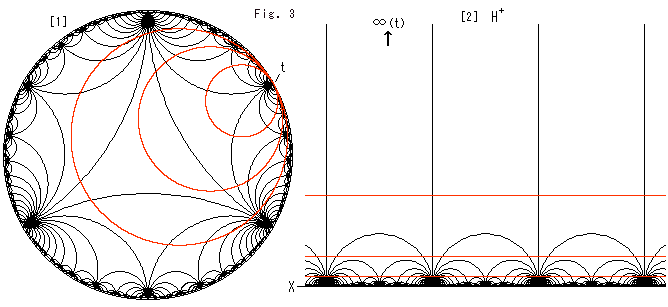 上のFig.3をご覧ください。
上のFig.3をご覧ください。
見やすくするために、2次元で代用してみます。
[1]: 球体の代わりにポアンカレ円板に理想正三角形を敷き詰めました。 円板ですが、球体だと想って見てください。 中にある理想正三角形も理想正四面体だと想って見てください。 赤い円は、点tで円板の周と共有点tをもっているホロサイクルです。 これもホロスフィア(球面)だと想ってください。
このホロスフィアは、ぴったり詰まっている理想正四面体を切っています。 つまり、ホロスフィアの面には、無数の理想正四面体をその頂点をそろえて切った切口が並んでいるのです。
[2]: [1]を上半平面上半平面 に移したものです。 見やすくなるように、点tを上の方の無限遠にとって変換しています。 この上半平面
に移したものです。 見やすくなるように、点tを上の方の無限遠にとって変換しています。 この上半平面 も上半空間H3+だと想って見てください。 赤い水平線は、理想正四面体を切っているホロスフィアです。 [1]でのホロスフィアの半径が大きくなると、赤い水平線はX軸の方へ降りてきます。
も上半空間H3+だと想って見てください。 赤い水平線は、理想正四面体を切っているホロスフィアです。 [1]でのホロスフィアの半径が大きくなると、赤い水平線はX軸の方へ降りてきます。
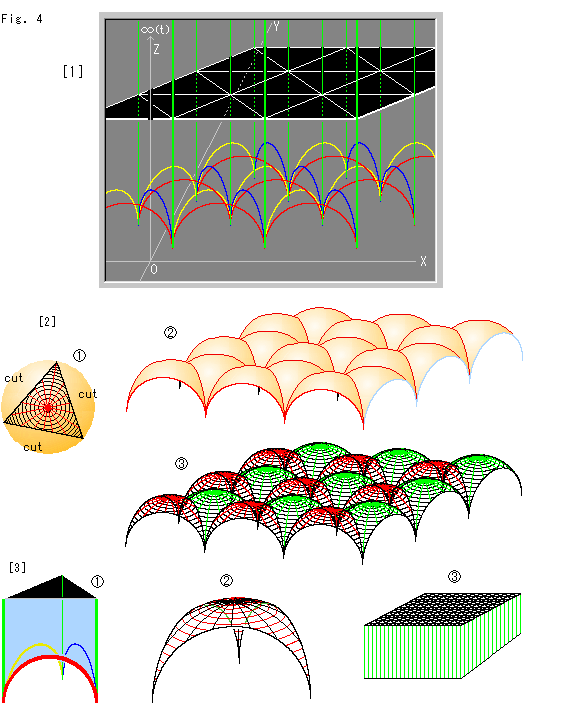
Fig.4をご覧ください。
[1]: 球状のままでは図を巧く描けないので、考え方の見通しをよくするためにポアンカレの上半空間H3+を利用します。 Fig.3の[2]の3-D版です。 底面が球面である正三角形の三角柱が敷き詰められています。 その一つ一つが理想正四面体です。 頂点の1つが上の方の無限遠(点t)へ向かっているものだけを描いて、他は省いています。 浮いて見える黒い平面がホロスフィアの1つです。 これは平面として描かれていますが、ホロスフィアとよんでおきます。 ホロスフィアは、理想正四面体を切っています。 白い三角形は、それぞれの四面体の切口です。 正三角形ですから、辺角が60 にそろっていることも、ひと目でわかります。
にそろっていることも、ひと目でわかります。
上半空間の床であるXY平面は、無限に広がっているユークリッド平面です。 もっとも、距離はその平面の上に立つ半円に沿って測る約束です。
[2]: 三角柱の1つを真上から見ると、底面は半球面を正三角形に垂直に切り落としたもので、 のようになっています。
のようになっています。  は、底面だけを取り出したものです。
は、底面だけを取り出したものです。  は、交互に色を換えて経緯線のスケルトンで描いたものです。
は、交互に色を換えて経緯線のスケルトンで描いたものです。
[3]: 三角柱の1つを取り出すと のようになっています。
のようになっています。  は、その底面を拡大したものです。(球面正三角形ではありません。)
は、その底面を拡大したものです。(球面正三角形ではありません。)
このテントを張ったような底面の下は空隙になっているので、当然そこにもFig.3の上半平面 のように理想正四面体を埋めていくことができると思えますね。 しかし、どう描けばよいのかわかりませんので、空いたままにしています。
のように理想正四面体を埋めていくことができると思えますね。 しかし、どう描けばよいのかわかりませんので、空いたままにしています。
でも、つぎのように考えます。 Fig.3で見ると、描く理想正三角形の大きさが、円板上ではひとりでに定まりますが、上半平面 上では適当にとるほかありません。 Fig.1の球体とこの上半空間H3+が、それと同様な関係になっています。 そこでまず、無限個の三角柱が立っていると想うことにします。 そしてその時は、床面の空隙はなくなるのだとします。 つまり作図的には、三角柱が十分細くなって空隙がなくなっているのです。 そのイメージを描くと、
上では適当にとるほかありません。 Fig.1の球体とこの上半空間H3+が、それと同様な関係になっています。 そこでまず、無限個の三角柱が立っていると想うことにします。 そしてその時は、床面の空隙はなくなるのだとします。 つまり作図的には、三角柱が十分細くなって空隙がなくなっているのです。 そのイメージを描くと、 のようになります。 しかし、作図的にはそうであっても、無限個の三角柱を用いたとしても、空隙が完全になくなるとは考えられません。 このあたりのことをどう始末すればよいでしようか? このことを気遣うなら、Fig.1に戻って想像をたくましくするほかありません。
のようになります。 しかし、作図的にはそうであっても、無限個の三角柱を用いたとしても、空隙が完全になくなるとは考えられません。 このあたりのことをどう始末すればよいでしようか? このことを気遣うなら、Fig.1に戻って想像をたくましくするほかありません。
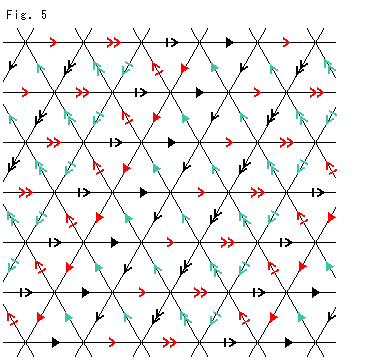
Fig.5をご覧ください。
Fig.4の平坦なホロスフィアを真上から見てみます。 理想正四面体の面が貼り合わされているものして、辺に矢印を付けたものです。
これこそ、8字ノットの補空間の展開図だといわれているものです。
でも、どうしてこんなものが展開図なのでしようか?
これは前に見たトーラスをつなぎ合わせものにほかなりません。 一般のトーラスをつなぎ合わせたものも、前に見ました。
展開図は、
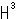 / [面と面の同一視を与える等長変換たちの生成する群]
/ [面と面の同一視を与える等長変換たちの生成する群]
= [面と面の同一視でできた空間] 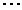 (*)
(*)
だそうです。 空間(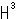 )を群でワルとか、生成する群って何のことでしようか?
)を群でワルとか、生成する群って何のことでしようか?
**************************************************
ちょっと振り返るなどして、話しはちりじりになりますが、まさぐってみましよう。
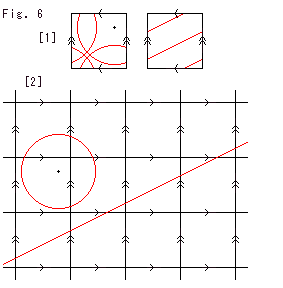
Fig.6をご覧ください。
[1]: 正方形のトーラスの上では、円や直線はこんな風になるのでしたね。
[2]: 1つの正方形を基本領域とよんで、格子状にならべたものです。 この上でなら、図のように描いて[1]とおなじことを表現できるのでした。
この[2]の格子は、同じ矢印の辺の上の点は、たがいに移りあえるのです。 格子線上の点は、格子線上から格子線上へと平行移動できるということです。 (格子線で囲まれた内部の点は、他のところへ勝手に移ることはできません。) そして、この平行移動は群をなすので、上の(*)にならうと、
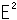 / [辺と辺の同一視を与える平行移動たちの生成する群]
/ [辺と辺の同一視を与える平行移動たちの生成する群]
= [辺と辺の同一視でできた空間]
と表現できます。 "/ "は、小学校で習った割り算ではありません。 ただ、このように書くだけです。 しかし、ワルと呼称されています。 (それは、商空間とかいったものがあるからでしよう。 私たちは、そんなところまでは及びつきません。)
そして、この[2]の格子がトーラスの展開図だといえることになります。 これで、補空間の展開図とはどんなものを指しているかがわかりました。
ふつうの展開図では、展開する元の図形を想像することは比較的簡単です。 しかし、8字ノットの補空間の場合は、Fig.5が展開図だといわれても、なかなか展開元のイメージを捉えることができません。 Fig.6に似たことをFig.5でやろうとしても、巧くいきません。
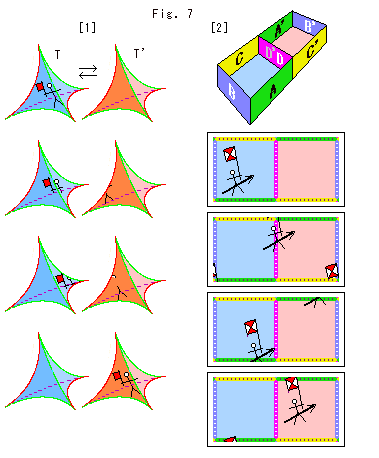
Fig.7をご覧ください。
私たちの武器であるイラストではどうでしようか。
[1]: 2つの四面体T,T'をならべて、それらの面と面が貼り合わされているものとして、そこに住む人の動きを描いたものです。 この動きと似た絵をこれまでにも描きましたが、ここでは四面体と四面体です。 面と面が貼り合わされている様子が、いま一つ見てとれませんね。 それに、辺の向きが考慮されていません。
[2]: 面のことだけをとってみたものです。 面Dと面D'を張り合わせた隣り合う部屋です。 四コマは、それを上から見たもので、同じ色の壁が同一視せれています。 この絵では、辺に相当する柱を色分けすることができません。
このように、私たちのイラストも無力です。 けれども、想像力のいくぶんの糧にはなるでしよう。
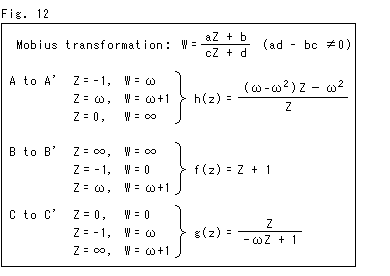 Fig.8をご覧ください。
Fig.8をご覧ください。
前にも書いた2つの理想正四面体の貼り合せの式です。 変換式 hの 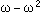 は
は 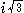 ですが、そう書いてないのは計算の便のためにです。
ですが、そう書いてないのは計算の便のためにです。
これらの変換 f,g,h は、変換fをしたものに変換gをほどこして、そのgfに変換hをおこなうといったものではありません。 それぞれの頂点が貼り合せされて行く先を表わしているだけです。 ですから、hgfのようなものが貼り合わされた結果だということにはならないのです。
一次変換(=メビウッス変換(Mobius transformation), ad - bc 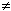 0)を元とする集合は、一次変換という演算(積)に関して群をなしています。 そして、一次変換 f,g,h の間には
0)を元とする集合は、一次変換という演算(積)に関して群をなしています。 そして、一次変換 f,g,h の間には
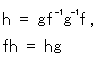 という関係が成り立っています。 これらはものの本でよく見かける形のものですが、いま群論に用があるとは思えませんし、私たちには馴染みがありません。 ここでは、単にこんな関係があるということだけにしておきます。
という関係が成り立っています。 これらはものの本でよく見かける形のものですが、いま群論に用があるとは思えませんし、私たちには馴染みがありません。 ここでは、単にこんな関係があるということだけにしておきます。
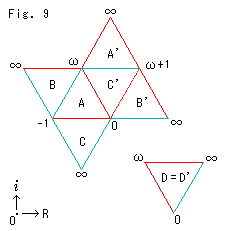 Fig.9をご覧ください。
Fig.9をご覧ください。
上半空間H3+にFig.8をイラスト化したものです。 面Aと面Cの頂点は全部がXY平面上にあるとしていますが、他の面の頂点は1つが上の方の無限遠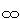 にあるとしています。 赤い辺は、それぞれ頂点の記号を一致させて、同一視されます。 緑色の辺も同様です。 無限遠
にあるとしています。 赤い辺は、それぞれ頂点の記号を一致させて、同一視されます。 緑色の辺も同様です。 無限遠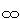 は1点になります。
は1点になります。
 Fig.10をご覧ください。
Fig.10をご覧ください。
うろうろしてはみたものの、バッチリとしたものは掴めませんでした。 けれども、8字ノットの補空間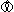 (= T U T' - V) を観念的に描いたこの図もまんざら不合理ではないと感じられてきたではありませんか。
(= T U T' - V) を観念的に描いたこの図もまんざら不合理ではないと感じられてきたではありませんか。
この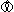 の中は双曲空間H3全体です。 その外側については、まったく考えません。 Fig.4やFig.5では、2つの理想正四面体が貼り合わされているものとして双曲空間全体に展開して描かれています。 つまり、貼り合わされた2つの理想正四面体としては同じで、図による表現が違うだけです。 展開してということも肯けますね。
の中は双曲空間H3全体です。 その外側については、まったく考えません。 Fig.4やFig.5では、2つの理想正四面体が貼り合わされているものとして双曲空間全体に展開して描かれています。 つまり、貼り合わされた2つの理想正四面体としては同じで、図による表現が違うだけです。 展開してということも肯けますね。
 Fig.11をご覧ください。
Fig.11をご覧ください。
補空間を得る一連の過程です。 ノットKは頂点Vとして(as V)切り捨てられ、2つの四面体はポアンカレ球体の中で理想正四面体に整形されます。 そして、抽象的に貼り合わされて、もとの補空間 S3 - K と位相同形な新しい補空間 T U T' - V を得ます。
一方、2つの四面体を貼り合わされているものとして(regarded as glued)、上半空間H3+内を切るホロスフィア上で見ると、展開図(developement)が得られるというものです。
かくて、私たちは8字ノットの補空間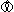 を“見た”といえることになりました。
を“見た”といえることになりました。
[前章] [次章] [目次]







 Fig.8をご覧ください。
Fig.8をご覧ください。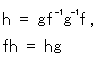
 Fig.9をご覧ください。
Fig.9をご覧ください。 Fig.10をご覧ください。
Fig.10をご覧ください。 Fig.11をご覧ください。
Fig.11をご覧ください。