8字ノットを抜いた空間が双曲空間だというのなら、ユークリッド空間から8字ノットを引き抜きさえすれば、双曲空間が得られると考えられます。 しかし、それは8字ノットの抜け殻からなる四面体の抽象的な貼り合わせ過程を経てのことです。 そうすると、得られた双曲空間は具体的なものではないわけですね。
ずいぶん色々と見てきました。 総括しようとするのですが、むずかしいですね。 雑感をひろっておくだけにしておきす。
* * * * * * *
平行線は本当に交わるのでしようか。
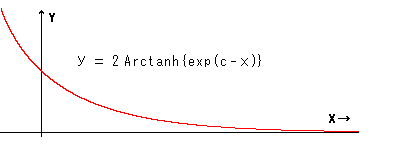
双曲的平行線のXY表現です。 この曲線を右の方へどんどん辿って行くと、どうなるでしようか。 簡単のために、曲線をふつうの双曲線だとして
とします。
このxを限りなく大きくしていくと、yは限りなく小さくなります。 yがゼロになれば、おしまいということにします。 ところが、xがふつうの実数なら、それをどんなに大きくてもyは決してゼロにはなりません。 そうすると、終わりがない。 xをさらに大きくする余地がいつまでもあるということです。 そこで、この余地がなくなる極端なx(実数かなにかわからないもの)が存在すると仮定して、それを無限大
と名ずけます。 つまり、
です。 よく、等号"="はいけない、矢印を用いて
と書くべきだといわれることがあります。 でも"
"だと、xが無限大に達するのかどうかはっきりしません。 仮に、有限のとこからきて、ずるずるとに達するのだとすると、そこから先を考えたくなります。
この議論を避けるために、ifのあとの x = は、xがふつうの実数から架空のに突然変異したものだとします。 無限大には淵はないのです。
射影幾何ではこれが巧妙に解決されているのを見ました。 一方、８字ノットの話しでは無限大の議論はまったく忘れられていました。 みんな、ご都合主義だという他ありませんね。
* * * * * * *
それにしても、気になることが一つ残っています。 測度論とよばれているものです。
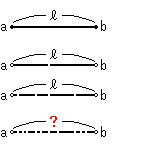
左図で線分abの長さ
は = ab です。 両端がない開線分であっても、 = ab です。 途中に無限小のギャップがいくつかあっても、やはり = ab です。 実際、積分してみればそうなります。 けれども、無限小のギャップであっても、それが沢山あるときは怪しくなってきます。 測度論というのは、こんなことを集合で議論しているものです。
双曲幾何は、長さの幾何だともいわれていて、計量がはいっています。 その計量などと線分abの話しとの関係はどうなるのでしようか？
* * * * * * *
目で見ることにしつくこだわってきました。 それは、幾何学が見えるものから発展したからです。 たとえば電気など、そのものを見ることは最初から不可能です。 また、算術においても数というものを見ることはできません。 それでいて、不可視であることにさほど不満を感じません。 要は慣れの問題だといえますね。
しかし、科学者はつねに目で見ることを追っています。 科学発展の原動力です。 ですから私たちは、実際の双曲的非ユークリッドの世界を見ようとすることを、原理的に不可能だとあきらめてはならないと信じます。 現に最近、磁石の中を通る磁力線の写真が公開されました。 いつの日か、双曲的非ユークリッドの世界も自分の目で見ることができるにちがいありません。
ところで、波乃光子の裁判記録が朝永振一郎の「量子力学的世界像」にあります。 見えないものの話しです。 ひょっとしたら、双曲幾何もこれと同じ穴のムジナかも知れません。 一読されるとよいでしよう。
* * * * * * *
８字ノットという言葉をはじめて聞いて、二週間後のことでした。
サーストンに訊ねました。（彼は、私が素人であることを知っています｡）
Ｑ： トポロジーでは、距離を気にしない。一方、幾何には距離が必要である。
あなたの幾何化では、新しく距離の定義をするのか。
Ａ： ノー。それは、英語から日本語への翻訳のようなものだ。
また、フランシスに訊ねました。
Ｑ： なぜ、８字ノットから双曲幾何が出てくるのか。
Ａ： Whyときかずに、Howと問うべきだよ。
* * * * * * *
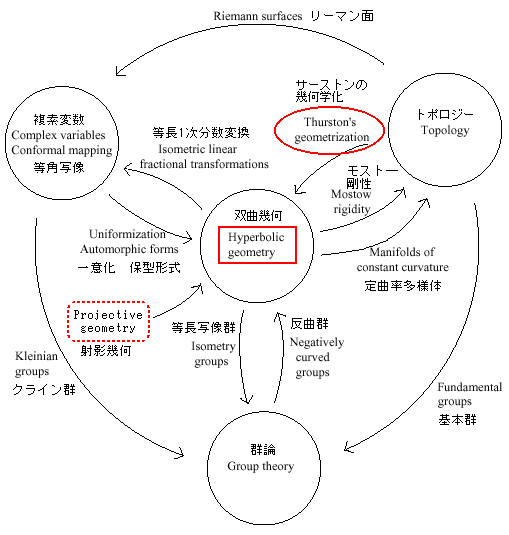
双曲幾何のひろがり:
下のチャートは、カノン、フロイド、ケニオン、パリの４氏による双曲幾何より得ました。 赤い囲みは、私たちが勝手に付け加えた関心のあるところです。
* * * * * * *
おわりに、絵をいくつか。
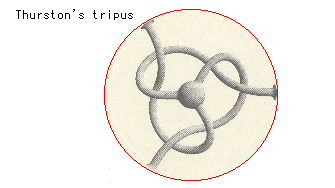
サーストンの３本足のタコ(tripus)とよばれている８字ノットの化けものです。
上半平面に描かれたベリルの芸術作品です。
双曲ジャングルジムと名付けられた早川氏の作品です。
本文の終わり