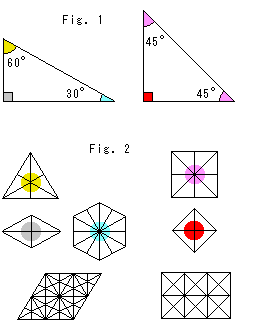
In an ordinary plane we can tile with congruent triangles, but this can be done with only two types of triangles, as shown in Fig. 1.
The internal angls A, B and C of a triangle on Euclidean plane are
A + B + C = 
.
As shown in Fig. 2, it is necessary that congruent corners are gathered at a point without any gap or oubling for tiling. So the internal angls A, B and C must be
.
These natural numbers are limited to
, 
, 
= 2, 3, 6 or 2, 4, 4.
To agree with it, all you have to do is make some paper work.
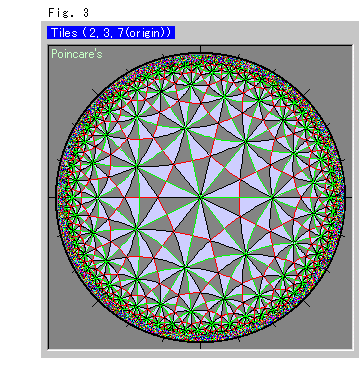
In the Hyperbolic Non-Euclidean World, internal angles A, B and C are
A + B + C < .
Therefore, there are countless natural numbers , and (>0) that satisfy the above expression with 
. We can tile any triangles with these natural numbers.
However, we do not have a choice of triangle size because angles A, B, C and natural numbers , , are inseparably related to each other. And the length of sides are determined if angles are defined. So that we can not choose the size of a triangle in common shape.
Triangles in Fig. 3 are of = 2, = 3, = 7. Such a trangle is called 2-3-7 triangle. It is a tessellation they say. It reminds us pictures drawn by M.C. Escher (1898-1972). He was a painter but he was much ahead of mathematicians for visualization of infinity. Our mind is attracted to infinity by his pictures.
As to Fig. 3 we use reflection that is like axial symmetry in the Hyperbolic Non-Euclidean World. If we invert a triangle, invert it again (front side up), and repeat this continuously, we can tile fully. The edge of the triangle is used as a turning axis. All the triangles are congruent. Let's suppose the colored side is the front, then the colorless side is the back.
Though we said "tile fully", the 2-3-7 triangle is finite so that it never arrive at the edge of disk no matter how we continue.
We can find congruent meshes in the tiling with 2-3-7 triangles. Fig. 4 below shows some of them, red framed regular heptagons, green framed regular triangles and black framed rhombbuses.
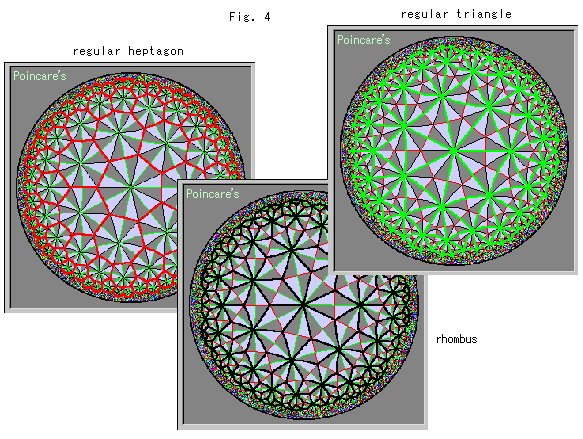
We could draw these pictures to look better, but, to tell the truth, we finished the edge with mosaic because our computer doesn't listen to us. And because, even if it does, it would take an infinite amount of time.
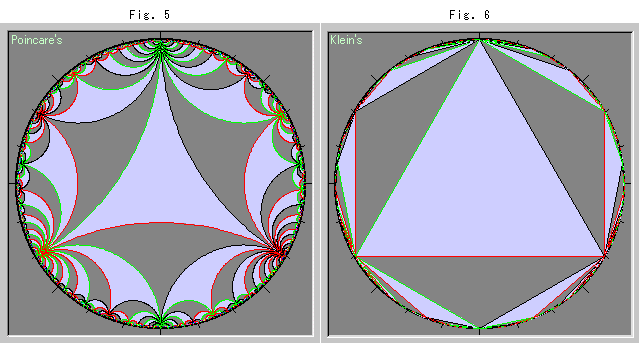
Fig. 5 and Fig. 6 above show tiling with ideal triangles. The ideal triangle is a triangle that every vertex extends toward infinity. The length of sides become a, b, c 
that is, every interior angle A, B, C 0 (= 
) . And the area becomes - (A + B +C) .
Fig. 5 is of Poincare's disk and Fig. 6 is of Klein's disk. They look quite diffrent from each other, but all the triangles of both figures are congruent. We can get an ideal triangle on Klein disk if we draw three straight lines that connect three pairs of vertices of an ideal triangles on Poincare disk.
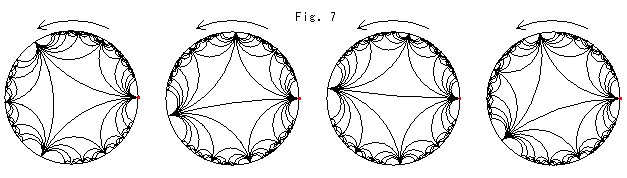
Fig. 7 below is four frames from an animation of ideal triangles created by Makoto Sakuma. The vertices at the right end (red spot) of each disk are fixed. A new triangle apperas at the end ponit and it turns. A turned triangle disappear at the end alternately.
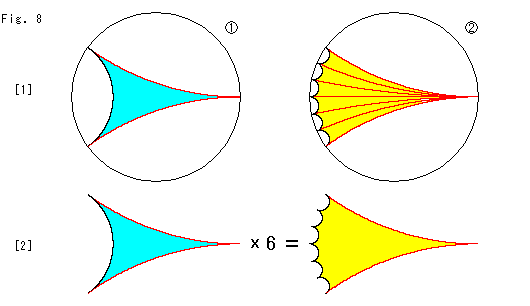
Look at Fig. 8.
As for ideal triangles, let us assume that all interior angles are zero and length of all sides are infinity. In that sense, all ideal triangles are regular triangles.
[1]: 
is an ideal triangle. 
is six of ideal triangles and the outer red sides are the same as that of . Since all ideal triangles are congruent, every yellow triangle is identical to the sky blue triangle.
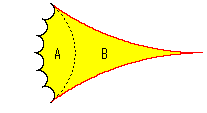
[2]: From the point of view of area, six times of the sky blue triangle equals the yellow figure in the right. Every interior angle of the yellow triangle is right-angled so that we can call the yellow triangle "zero-angled heptagon". If we cut it along the dotted line as shown right, A will be a hexagon and B will be an ideal triangle that is the same as the sky blue triangle.
Usually hyperbolic trigonometry is not applicable to ideal triangles. Illustration here helpt us understand intuitively without such a trigonometry. That is a distinctive feature of an ideal triangle.