Ch. 13  Parallel Translation (1)

      Parallel translation in the Euclidean world is the term used to describe the parallel moving of all points on a figure by an equal distance, as shown in Fig. 1. The figure never changes in shape or size when parallel translation is carried out. The figure is congruent in every way. What will happen in the Non-Euclidean World if we move a triangle? Let's experiment by drawing some pictures.

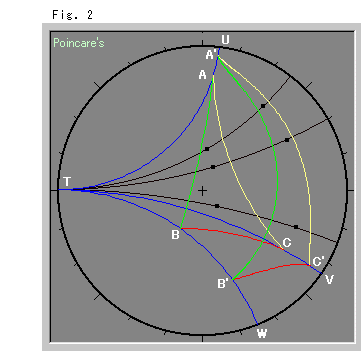
      Look at Fig. 2. First let's move a triangle along parallel lines. We will draw three parallel blue lines , TV and TW that go through three vertices A, B and C of a triangle with common point T. The black parallel lines go through points on triangle ABC. Imagine there are countless parallel lines, which go through every possible point on triangle ABC.

      We moved all the points on triangle ABC along parallel lines by equal (hyperbolic) distance. Oh, how different the new figure A'B'C' is from the original triangle ABC! It is not a triangle at all. Lines A'B', B'C' and C'A' are no longer straight.

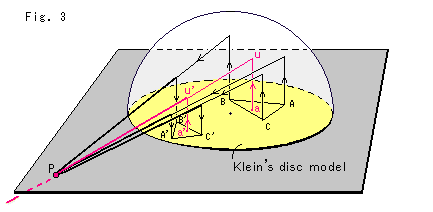
      Now, let's use reflection and keep things congruent. We use a hemisphere as shown in Fig. 3. The yellow base is Klein's disk model.
First, we add two points a and a'. Point a is on the original triangle ABC, and point a' is the new point (location) of a after it was moved. We raise points a and a', and get points u and u' on the hemispher. See the red lines on Fig. 3. When we draw a straight line that passes through points u and u', it goes through the gray plane at point P. Point P is called the "pole of reflection".
Now, we move all other points on triangle ABC. Let us take vertex A for example. We raise it up to the surface of the hemisphere, and then draw it in the direction of pole P. Now follow the black line. Point A goes under the hemisphere and reaches its surface again, where point A drops back to the yellow disk. The landing point is a new vertex A'. (We will do the same thing on a single plane later.)
      In reflection a figure is inverted, so we are actually carrying out reflection twice here. If the figure is on Poincare's disk, we change it into Klein's disk, and then change it back to Poincare's disk after moving it.

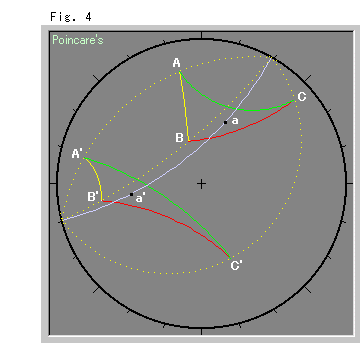
      Look at Fig. 4. Triangle ABC moved and became triangle A'B'C' by reflection (twice). The yellow dotted lines are the loci of three vertices A, B and C.
The new triangle A'B'C' is perfectly congruent to the original triangle ABC. The loci are not straight but are equidistant. We may think equidistant lines are parallel lines for parallel translation. However, the moved distances AA', BB' and CC' are not equal.
Nevertheless, it can be said that this movement is a hyperbolic parallel translation. We will see this again in chapter 17.




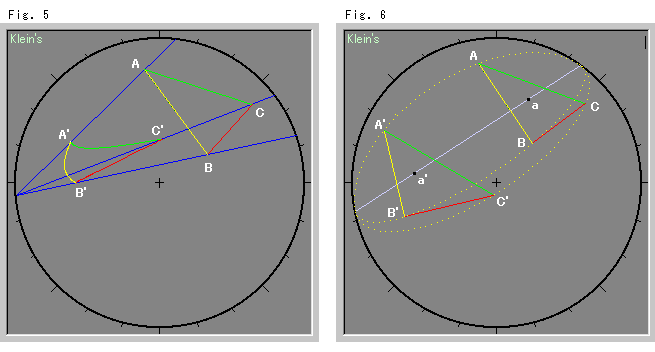
  Fig. 5 and Fig.6 below are experiments on Klein's disk. Fig. 5 is in the case of Fig. 2, and Fig. 6 is that of Fig. 4. In Fig. 6 angls and the lengths of the sides look different but, of course, the two triangles are congruent.