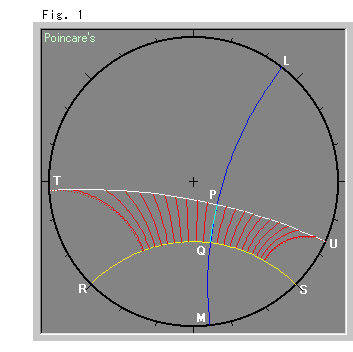
Look at Fig. 1.
The two straight lines RS and TU are separate from each other. They are not parallel lines because they have no common point at infinity (the disk edge). Nevertheless, they are separate from each other. In Euclidean plane, there is not a single pair of lines that neither intersects nor is parallel. On the plane in the Hyperbolic Non-Euclidean World, as you see, such lines exist. We call these lines ultraparallel lines.
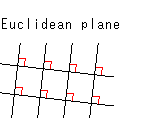
In Euclidean plane, we can not draw a straight line that cuts perpendicularly non-parallel lines. But on the plane in the Hyperbolic Non-Euclidean World we can. It is only one, though. The blue straight line LM is the common perpendicular line. In the Hyperbolic Non-Euclidean World, however, we can not draw just any common perpendicular line as you see below. In other words, we are not able to draw lattices (orthogonal grid pattern).
The red lines are simply for your convenience in observation.
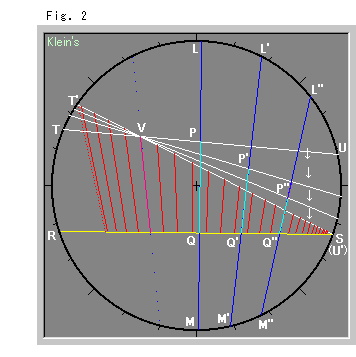
Look at Fig. 2. This time we used Klein's disk model to make these concepts easy to see.
Fix a point V on the straight line TU and rotate it clockwise to straight line T'S. When this is done, the common perpendicular line LM moves toward point S as L'M', L"M", etc. At the same time, the length d of PQ is shortened to zero as P'Q', P"Q", etc. When endpoint U finally meets with point S, and straight line TU becomes straight line T'U', the common perpendicular line becomes a tangential line to the model disk. That is, the ultraparallel lines are now normal (hyperbolic) parallel lines.
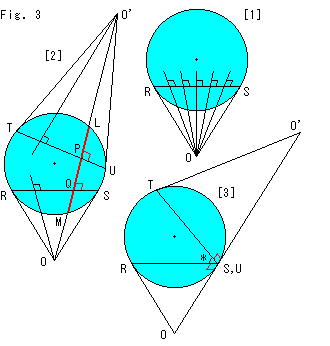
Look at Fig. 3.
This is how you can see the phenomenon in Fig. 2 by construction.
[1]: Klein disk has the chord (straight line) RS. We draw tangents OR and OS that contact the disk. Now all straight lines that cut the chord RS are perpendicular to it.
[2]: We can draw a common perpendicular line cutting ultraparallel lines SR and TU. It is the straight line O'-L-P-Q-M-O.
[3]: Chords RS and TU have a common point at infinity (disk edge) now. That is, they are forming parallel lines. Straight line OO' is perpendicular to both chord RS and TU but it is tangent to the disk and does not pass its inside. Angle RS(U)T marked "*" is zero. (We will occasionally talk about constructions.)