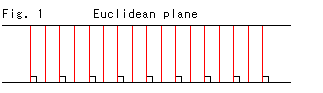
Fig. 1 shows ordinary parallel lines. In the Euclidean World, equidistant lines and parallel lines are the same. But in the Hyperbolic Non-Euclidean World, they are different. Equidistant lines are lines that have equal distance between them at all times, anywhere on the lines.
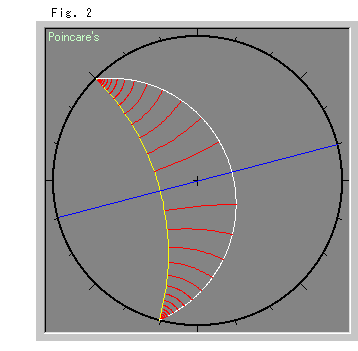
Look at Fig. 2.
These are equidistant lines on Poincare's disk. The equidistant line is a line that is equally spaced from a straight line. The white curved line is an equidistant line equally spaced from the yellow straight line. The red lines are perpendicular to the yellow line, and their lengths are the same. The blue line is just for your observation.
The equidistant line is not straight. On Poincare's disk, an equidistant line is drawn as a circular arc.
The white and yellow lines look as if they meet at infinity. They shouldn't change no matter where they go, should they? No, they never change, even at infinity, because they are not parallel lines, and by definition they are to be equidistant. But how can we see this to be true? Nobody can see the situation at infinity with his own eyes, just as it is impossible to do so with parallel lines.
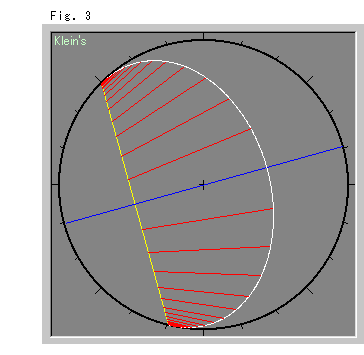
Fig. 3 is of Klein's disk. It is just for your comparison with Fig. 2. The white equidistant line is a part of the ellipse that is inscribed to the edge of disk.
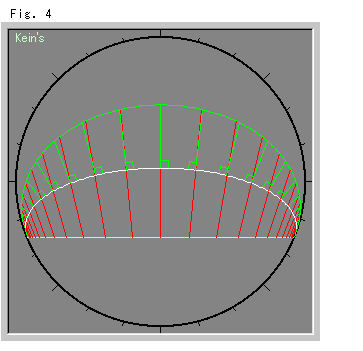
Look at Fig. 4.
On the Euclidean plane two equidistant lines with respect to one straight line are equidistant from each other. How about it in the Hyperbolic Non-Euclidean World? Klein's disk is good to distinguish a curved line and a straight line visually. So we used it. Both white and green lines are equidistant to the yellow straight line. Red lines are hyperbolic normals to the yellow straight line. Since the two equidistant lines are not straight lines, one is not an equidistant line to the other. But every distance between the green and white lines measured along each red segment is constant.
As a trial, we draw the green normals on the white line, and measured hyperbolic lengths of green segments. Naturally they are not constant.
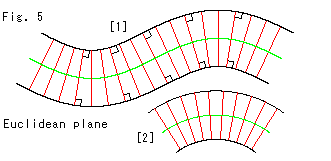
Fig.5 shows parallel curves on Euclidean plane.
Incidentally, let us see what is called parallel curves. They are curved lines that have common normal at every point on them.
[1]: The red segments are common normals but their lengths are not constant.
[2]: It is a part of a concentric circle. In this case, needless to say, lengths of all red segments are equal.
(Scroll and shake your screen up and down. The parallel curve [1] will snake.)
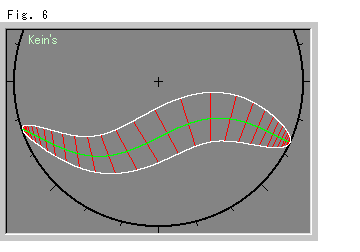
Look at Fig. 6.
What will happen if we draw parallel curves in the Hyperbolic Non-Euclidean World? In case of a concentric circle, the result shall be the same as in the Euclidean. It's not fun. On Klein's disk we draw similar curves to [1] in Fig. 5. First we draw the green line and we put the red hyperbolic normals with constant hyperbolic length. Then we follow the end points of the red segments and get the white curves. Well, it looks like a caterpillar eating infinity, doesn't it? Tangents of each white curve are not hyperbolic perpendicular to
red normals. Therefore white curves are not parallel curves. But in case of the figure they are quite close to parallel curves. Anyway parallel curves in the Hyperbolic Non-Euclidean World become like this figure.