In the Hyperbolic Non-Euclidean World angle and distance depend on each other. Here we see this with the formula of parallel angle.
The formula of a parallel angle, as described in Chapter 7, is
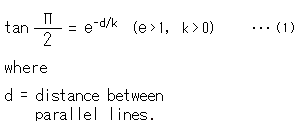
d is hyperbolic distance between parallel lines. k is a constant depending on unit distance. e is indefinite constants. We are going to take a look at them with parallel angle 
now.
In formula (1) it is called standardization that we let k be 1, and e be the base of natural logarithm. Hereafter, we will use standardized one unless otherwise stated.
Suppose k is simply one. Can you imagine what will happen if that means 1 meter in our daily space? If k is 1 trillion light year, we may say the universe including all celestial bodies is Euclidean space.
Look at Fig. 1.
Let us see how length and angle depend each other in the formula (1) of parallel angle. Here we use a word "length" rather than "distance".
[1]: It shows the relation between angle and length d. The point with asterisk "*" on the curve is where angle is 
/4 and legth d is 
(= 0.881).
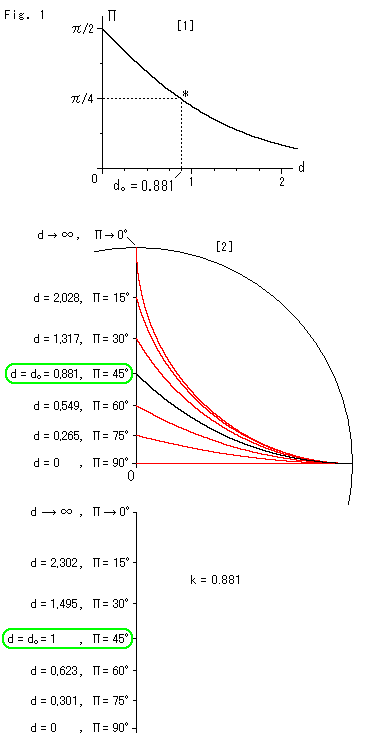
[2]: Angle performs on the vertical line that length d is measured. So we use the first quadrant of Poincare disk. All curves are parallel lines. The black curve is when parallel angle is /4, that is at asterisk "*" in [1]. (The vertical axis is opposite from [1] with respect to .)
Thus, when an angle is settled, distance shall be fixed, and vice versa. Therefore the absolute unit of length, which we talked about a bit, is naturally settled. For intance, we can make the unit length that has geometric meaning.
[3]: We have assumed that k is 1 (standardized). But let us take d/k instead of d, and let k be 0.881. Then, when is 45
becomes exactly
= 1 .
J. Bolyai and Gauss thought that there were numberless geometries depending on the value of k, and that the exact value of k in our actual space was to be defined. And they were troubled because they felt that hyperbolic geometry would not be complete unless an absolute unit length was found.
Also some people judged that geometry having such a thing can't stand because it is inconsistent. It isn't easy for us to think of absolute unit length, is it?
Today, however, mathematicians seem to be completely disinterested in it. They do not care about physical matters. Lobachevsky didn't feel so uneasy about it. We don't either. But, putting aside the concept of physical space, the idea of an absolute unit of length is very attractive, isn't it? Because the unit length in the Hyperbolic non-Euclidean World can be desided as what has geometric meaning. However, nothing new comes out even if it could be done.
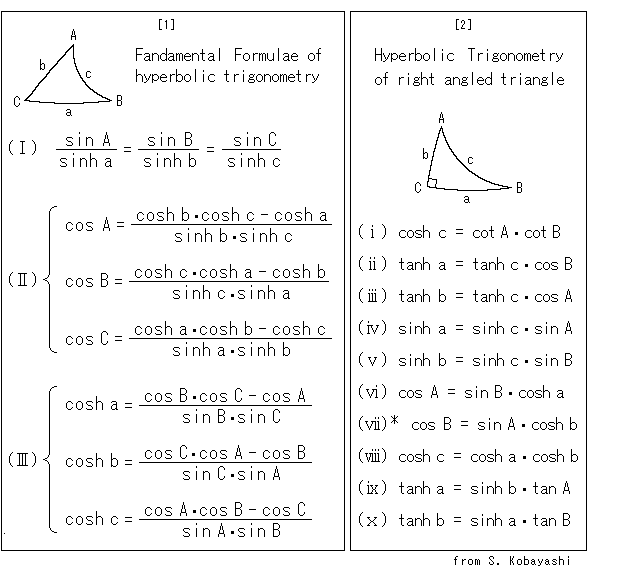
Two boxes at the left are formulae of hyperbolic trigonomrtry. It is usually not applicable, as well as ordinary trigonomrtry, if an angle or a side is zero. It is not applicable either if length of a side is infinity or toward infinity.
[1]: They are fandamental formulae.
(
) is similar to the law of sine in Euclidean trigonometry. It is much more similar to that of spherical trigonometry.
(
) is similar to the law of cosine in Euclidean trigonometry. It is much more similar to that of spherical trigonometry.
(
) is the surprising formulae that define length by angle only. They are not relations of one-angle-one-distance like the formula (1) of parallel angle.
[2]: They are major fomulae of right angled (C = 
/2) triangles in particular.
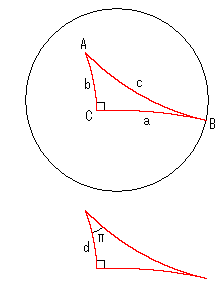
Now we pay attention to the formula 
marked with "*" that has neither a nor c appalently. See the figure right. It is a right angled triangle ABC on Poincare disk. The vertex B is on the disk edge so that two sides a and b are in parallel. And B 
0. So let B be 0 and apply formula to this triangle.
Then we get 1 = sin A
cosh b .
Since angle A is a parallel angle now, we use for A. Accordingly we change b to d. Then, after transposition,
= 1/cosh d . 
(2)
This must agree with standardized formula (1) because the relation between angle and distance d.
Let us confirm it. First we standardize formula (1) with k = 1.
Squre both sides respectively, and fit them to
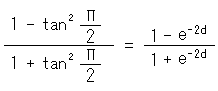
Then, it becomes
e disappeared into hyperbolic function tanh. Transform this expression to
That is, 
.
Since both sin and cosh d are positive, we can extract square root them. Then, we get formula (2). Therefore formula (2) and standadized formula (1) are equivalent.
Thus we can accept the formula of parallel angle with neither following Lobachevsky's way nor calculating on a model.
Formulae of hyperbolic trigonometry was found by Lobachevsky, and of course, it can also be proved with a model.
By the way, what do k and e affect models? Only scale of distance changes when they change. There are relations among k, e and parallel angle but patterns of curved line remains unchanged.
To see the trio of k, e and parallel angle click [k, e and parallel lines].