Lobachevsky assumed that parallel lines meet each other at infinity. How did he make it? Let's investigate to understand in our way.
Let us pick up some items from Euclid's Elements. The items directly related to parallel lines are:
Definition 23.
Parallel straight lines are straight lines which, being in the same plane and being produced
indefinitely in both directions, do not meet one another in either direction.
Postulate 1.
To draw a straight line from any point to any point.
Postulate 2.
To produce a finite straight line continuously in a straight line.
Postulate 5.
That, if a straight line falling on two straight lines makes the interior angles on the same side
less than two right angles, the two straight lines, if produced indefinitely, meet on that side on
which are the angles less than the two right angles.
(The above is quoted from http://aleph0.clarku.edu)
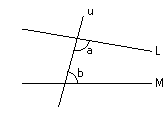
Our understanding of the fifth postulate is that;
In the figure right, u, L and M are finite straight lines (segment). If a + b < 
, then L and M must intersect each other on the side of a, b when u and L are extended enough.
In the particular case when a = b = pi/2, however, Euclid never said whether the two lines meet or do not meet. What a genius Euclid was! He cleverly escaped from infinity.
The Hyperbolic Non-Euclidean Parallel Postulate (or definition) is that;
However, Lobachevsky said nothing at all about either "straight" or "infinity". Moreover, he did not prove the non-contradiction of his geometry based on this postulate. He just discerned the truth and was convinced it was true. (Euclid himself, we guess, was in the same situation.)
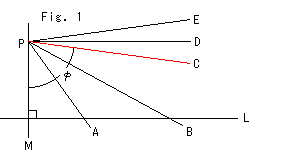
Look at Fig. 1 left.
Now let us see a key point in Lobachevsky's idea. Draw a straight line L and a point P (not on L). The straight line PM is perpendicular to straight line L. Draw radiating straight lines A, B, and C from point P. Lines under the red straight line C (such as straight lines A and B) cut across straight line L. Straight lines above straight line C (such as straight lines D and E) do not cut across straight line L on the right side of line PM.
Straight line C is special. It may or may not cut across straight line L, we do not know. Now assuming the existence of straight line C, we say that straight line C is parallel to straight line L. And angle is that Parallel Angle 
.
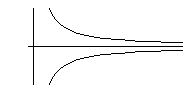
In ancient times, Proclus (A.D. 410-485) wondered about the following:
When a straight line is right angled to two other straight lines, if we exchange the right angle for an acute angle, the two straight lines tilt toward each other. Do the two tilted straight lines definitely cross when expanded? There exists a fact that two certain curved lines that tilt toward each other never meet, no matter how far they are extended. (He thought these curves might be hyperbolae that sandwich an asymptote.) Therefore, two straight lines may never meet, even if they are tilted. What keen insight he had!
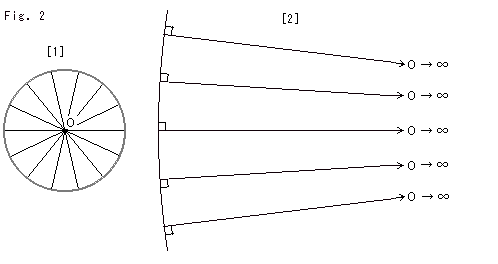
Look at Fig. 2.
Let's go back to Lobachevsky.
[1]: Place a point on the circumference of circle O, and then "kick" the center O to infinity.
[2]: The circumference will then stretch straight and the radii will have infinite length as shown.
Lobachevsky named this circle the limit circle. He assumed that [1] is possible and [2] is the result of [1].
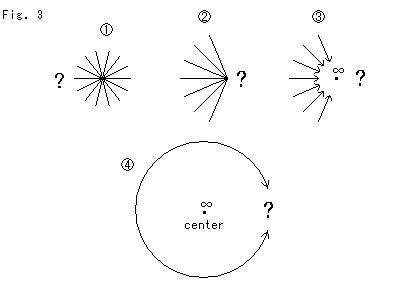
Look at Fig. 3.
Here let's introduce a bit of naive thinking.
: Is the situation at infinity like this?
The answer is "No", because nothing can exist beyond the center if it is at infinity.
: Then, is the situation like this?
No. First we must realize that there is no such thing as a place or location at infinity. If there were any location called infinity, it is not actually at infinity because we can think beyond the location.
That is to say that no one is able to describe the actual situation at infinity. We are free to image that infinity is in such a "direction". However,
We must not image the location of infinity.
We have no freedom of even imagination as far as the location of infinity is concerned. Because we cannot help but indicate beyond the location.
: How about this?
Never! Don't be agaist what is said now. Even if the arrows are at a finite position, it is no good because all the radii must be symmetrically equal around the center. If the figure is supposed to show a location near infinity, it is absolutely nonsense because, as far as infinity is concerned, we cannot say, "near" or "far".
But I have heard that it is thinkable what is called the neighborhood of infinity. Why don't you clear it up?
Well, yes. But no one in the world has not yet done it for hyperbolic geometry.
: In the end we are totally at a loss, aren't we? A circle is a closed loop. If the center is at infinity, the circle will be non-circle unless a territory exist beyond infinity. Is there extra infinity?
That is a hard question. Lobachevsky said "If we push the circle center unlimitedly to infinity, it will be --- at the limit---", we guess. Words "unlimitedly" and "limit" are strictly defined by 
logic. But it is still vague for us to understand intuitively. We can never arrive at infinity whatever far we go unlimitedly. Because it is infinity. Therefore [2] of Fig. 2 is a figure under way to infinity. It never ends. Lobachevsky thought such a limit in progress. In short the limit circle is a circle forever. The value of its radius and diameter can be
It is unlimited finite value. It has neither name nor symbol for some reason. So let us name it "Great Number" and denote it by 
. Great Number can be set as large as you like. But there is no infinity next to it. The end point of finiteness is not infinity.
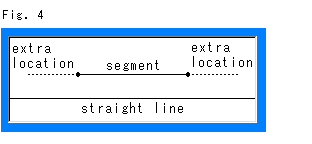
Look at Fig. 4.
A segment has end points. An open segment can also have end points as boundaries. We can extend a segment however much longer we wish, but never to infinity, since we can indicate the extra location both ends of the segment as shown. In general a straight line means a line with infinite length. The straight line has no end point at all. Therefore, a straight line is not an extended segment.
Let's go back to Lobachevsky and listen to him.
The following is our understanding of what he said, though not exact.
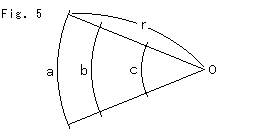
Look at Fig. 5.
Arcs a, b, and c are portions of concentric circles and represent length in Euclidean geometry.
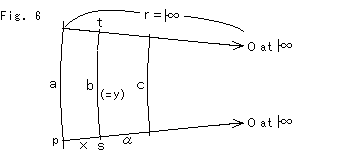
Now we push the center O toward infinity as shown Fig. 6. "toward infinity" means "never arrive at infinity". See symbls . The circumference goes certainly round the center O. Since radius r is Great Number, we can take the double value of r. a, b and c are regarded as strait lines but their length are not equal.
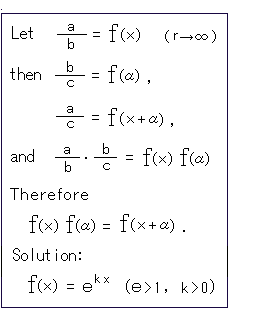
See the box at the left.
To keep things simple, let a = 1, k = 1 and e = base of natural logarithm.
b and c change according to a. k is constant and depends on a unit of length.
Now rewrite b to variable y.
Then
1/y = f(x) .
And we get
y = exp(-x) ---(*)
where
x = distance ps,
y = distance st.
This (*) is the revolutionary Lobachevsky's starting point.
According to the above-mentioned it is no trouble to let x = 
. In that case we can image like Fig. 7 and forget about around the center O without Great Number. In fact, infinity itself is not involved in hyperbolic geometry. Therefore it is not necessary for us to attend the dialogue in Fig. 3. It is presumed that Lobachevsky thought like this and established his axiom. That is, he founded "parallel lines meet each other".
The axiom is just an idea. And we do not say that Lobachevsky's is better than Euclid's. It is well known that we are free to choose either of them.
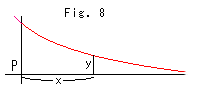
Fig. 8 at the left is of expression (*). It is a popular exponential curve. We do not say a straight line becomes like the red curve. Fig. 7 is drawn with straight lines but it is just a figure for think now.
Lobachevsky ingeniously used a sphere with an infinite radius and found that parallel angle. The sphere is called a limited sphere. And he deduced hyperbolic trigonometry. A geometry with that trigonometry is hyuperbolic geometry.
Thus hyperbolic geometry is completed. However, there is nothing to see concretely. In a talk about high dimentions or electrons we can image as is absolute matters. But in hyperbolic geometry we can draw somethings as above though they are not hyperbolic plane itself. Historically geometry is a visible subject, and seeing is believing. So they did not accept this abosute world as it is. It was a model that saved it.
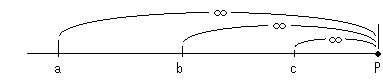
Yes, it is. We can draw infinity if we use a model! What we say "use a model" means to define the way of measurement of length. See the figure right. We can define distance so that from point a, b or c, whichever to point P is infinity. To be exact, it is incorrect what we said "We must not image the location of infinity because we cannot help but indicate beyond the location." There is nothing beyond the location if we make a good agreement on distance.
Therefore,
It is possible to imagine and draw infinity.
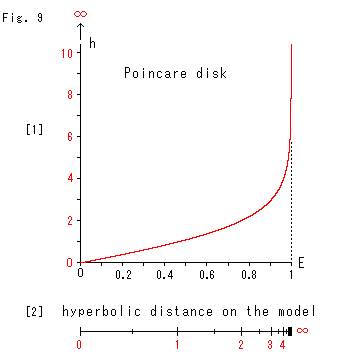
Look at Fig. 9.
Let us see distances from the origin of Poincare disk.
[1]: The red curve shows the difference between the two measurement of length. One is Euclidean distance E and the other is hyperbolic distance h. (The vertical scale is compressed to 1/10.) In hyperbolic measuring we get close to infinity when we start from any point inside to the disk edge (E = 1).
[2]: It is the raius of Poincare disk marked with hyperbolic distances. A mode like this is a compressor, isn't it?