So far in our study, we have seen some illustrations of the Hyperbolic Non-Euclidean World. In this chapter, let's see the most fundamental aspect of the Hyperbolic Non-Euclidean World.
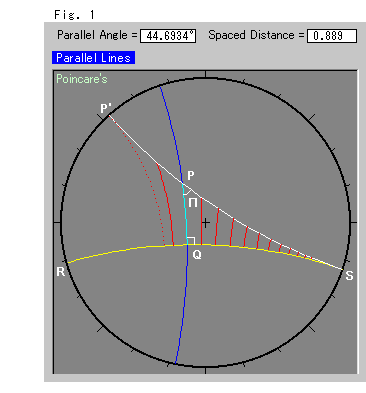
Look at Fig. 1.
The straight line RS and point P (not on RS) are given. The straight line P'S is drawn through point P. In the Hyperbolic Non-Euclidean World, the straight line P'S is a parallel to the straight line RS. They get closer and closer to each other when they go in the parallel direction to point S. They appear to have the common point S at infinity (model disk edge). The blue and red lines are perpendicular to the straight line RS, and the red lines are at regular intervals on RS (except for the dotted line that goes to point P').
Angle SPQ is called
Parallel Angle
which was named by Lobachevsky and is usually denoted by 
(Greek capital letter pi).
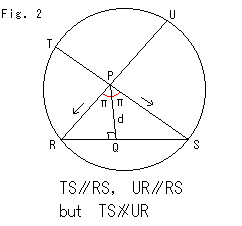
We can draw another parallel line PR. That is, there are two parallel lines with the given straight line RS through the given point P. Isn't it mysterious? Not really. Stay here in the Hyperbolic Non-Euclidean World a little longer.
Look at Fig. 2.
It is Klein's disk that we can see a straight line as a straight line. There are two straight lines TS and UR passing through point P that is not on the line RS. Both of straight lines TS and UR are parallel to the straight line RS. Each arrow shows the parallel direction of lines TS and UR respectively. In Euclidean geometry all parallel lines to one straight line are parallel each other. But lines TS and UR are not parallel each other. Because they have no common point on the disk edge that is infinity.
The formula of Parallel Angle discovered by Lobachevsky is
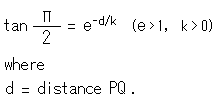
To keep things simple, let e be the base of the natural logarithm and let k be 1. (We'll discuss about e and k later.) The right side 
must be less than 1 because the parallel angle is less than 
/2.
Now, observe this formula carefully. Angle is the function of distance d !
First of all, we must accept that
Do you agree with this?
The angle and the distance are completely different in nature. Yet, they are jointed by equality sign "=". Some pioneers thought it impossible, and renounced it though they were very close to the formula. Lobachevsky, however, thought it quite natural just as universal gravitation that depends on distance.
The formula of parallel angle was found by Lobachevsky, J. Bolyai and Gauss independently around 1826.
Isn't it interesting how they got such a strange formula by only an assumption that parallel lines meet each other? However, let's not ask about it here, and rather let's pay attention to the fact that they established a relationship between length and angle that Euclidean geometry does not.
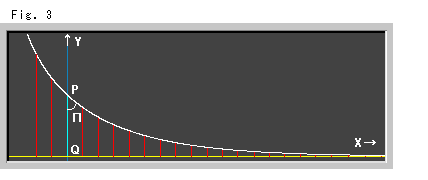
Look at Fig. 3.
This is a pair of hyperbolic parallel lines drawn on an ordinary plane with respect to XY-directions only. The yellow base line RS is set on X-axis, and the hyperbolic gap PQ of hyperbolic parallel lines is taken in Y-direction as it is. The red segments are at regular hyperbolic intervals. We can measure them with an ordinary ruler and find its hyperbolic length though they are only in XY-directions. The white curve looks like an exponential curve but it's not. We can also measure the parallel angle at any point on the curve with an ordinary protractor.
Well, do parallel lines really have a common point at infinity? It seems natural when we see what happens at the lower right portion of Fig. 3. How about you?
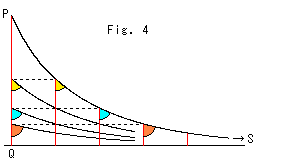
Look at Fig. 4. It is drawn just like Fig. 3. If we go forward to the common point S along the parallel line PS, the parallel angle gets bigger and closer to /2 by and by. And parallel angles in the same color are the same. It indicates, as far as parallel angles are concerned, to go to infinity is equivalent to go down to point Q. Going to infinity is going to zero!