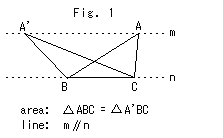
Fig. 1 to the left is the Equivalent deformation of a triangle, which you probably studied in elementary school. It stands in the Euclidean World, doesn't it? How about in the Hyperbolic Non-Euclidean World?
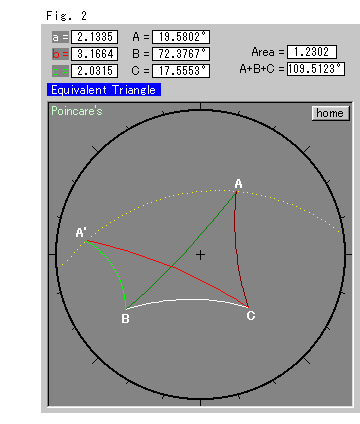
Look at Fig. 2 right. The side BC of a triangle ABC is fixed and the vertex A is movable. This time it is moved to point A' while keeping the hyperbolic area S of the triangle constant. This is an equivalent deformation. All of the numerical values shown at the top change with every movement of vertex A, except the area value, which remains constant. The dotted line is the locus of point A. It is neither parallel with the fixed side BC nor equally spaced from the straight line that passes points B and C. The locus is not even a straight line.
It is because that in the Hyperbolic Non-Euclidean World, the area S of the triangle ABC is calculated in a strange way:
- (A + B + C) . 
(1)
You see,
We cannot believe it right away. Where is this formula taken from? Well, in (Euclidean) spherical geometry, the area S of a triangle on a sphere with radius r is
((A + B + C) - ) . (2)
Lambert pointed out that hyperbolic geometry is an imaginary-spherical geometry, though he himself did not believe in hyperbolic geometry. If we replace radius r with 
(= 
), we will get the above formula (1).
It is not easy for us to imagine a sphere with a radius consisting of an imaginary number, is it? Well, we will see it later.
Look at Fig. 3.
We have seen some models of hyperbolic geometry. Now let us compare them with the model of elliptic geometry. The model of elliptic geometry is a sphere. It is inconvenient for us to compare it with a flat model of hyperbolic geometry. So we try to make a flat model of elliptic geometry.
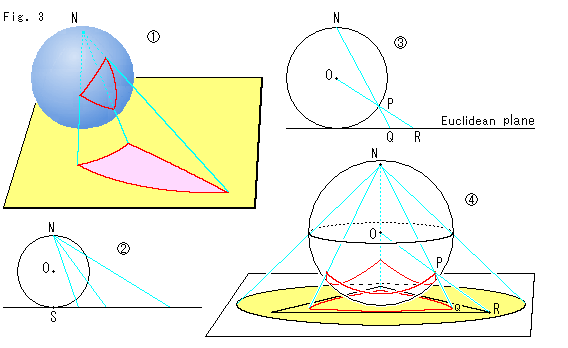
: The blue sphere on the yellow plane is a modele of elliptic geometry. A triangle on the sphere is projected from the north pole N to the plane.
: The plane is set horizontally and we view through the sphere with rays.
: We project point P from north pole N to point Q on Euclidean plane, and we also project the point P from the center O to point R on the plane. Such projection from north pole N is called stereographic projection, and the sphere is called Riemann's sphere. The projection from the center O of sphere has no name. So let us name it ball-core projection.
: We put a spherical regular triangle on the right bottom of sphere and project it to the plane, N-P-Q and O-P-R. We project the equator to the plane, too. The projected equator plane (yellow circle) is our disk model of elliptic geometry. However, it is on condition that we pay attention to the southern hemisphere only. Because antipodal points of Rieman's sphere are identified for elliptic geometry, and so we do not need the northern hemisphere.
Also we do not consider antipodal points on the equator for our disk model. Otherwise, our disk would become a plane in projective geometry. That is to say, our disk is open as well as the disk of hyperbolic gometry.
In conjunction with Euclidean plane, we agree on that ball-core projection is appropriate rather than stereographic projection. See chapter 3. So we project point R on the Euclidean plane to point P on the sphere, and then we core-project it to the original plane that becomes our model of elliptic geometry as point Q. Namely the sphere is a relay land between Euclidean plane and our model. The reason why we use stereographic projection is because it is conformal mapping and good for comparison with Poincare disk.
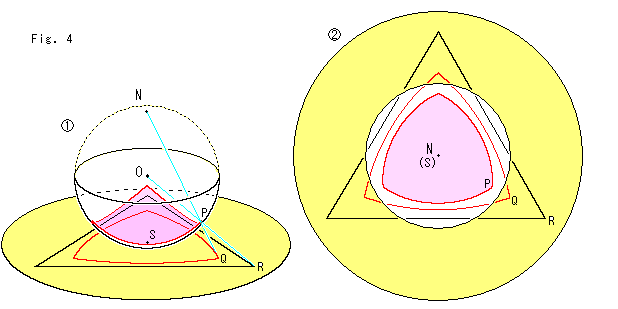
Look at Fig. 4.
: We tilted of Fig. 3 some more so that we can see the situation on the plane easily. We cut the sphere so that the only southern hemisphere remains. The frame of plane is omitted. The spherical triangle is dyed pink. The ball-core projection O - P - R forms the black triangle on the plane. The Stereographic projection N - P - Q forms the red triangle on the plane.
: It is the top view. The red triangle is equiangular to the pink angle. But the black angle is not so. The sides of red triangle is curved, but those of the black triangle are straight.
Thus we can move among three worlds, Euclidean plane, Riemann's sphere and our disk model of elliptic geometry. Stereographic projection is what is called conformal mapping so that an angle on the sphere and a projected angle on the plane are always identical. In core-projection no angle is kept unchanged but a straight line (great circle) on the sphere becomes a straight line on the plane. That is to say, two straight lines on Euclidean plane change into two great circles. And those two great circles are to be transferred to our disk model of elliptic geometry while keepig the angle of intersection.
The radius of our disk in this is double sized of the equator but we will draw it in the same size as Poincare disk. We chose a regular triangle just for easy drawing. Needless to say, the way of measurement (metric) on our disk is different from that of the sphere.
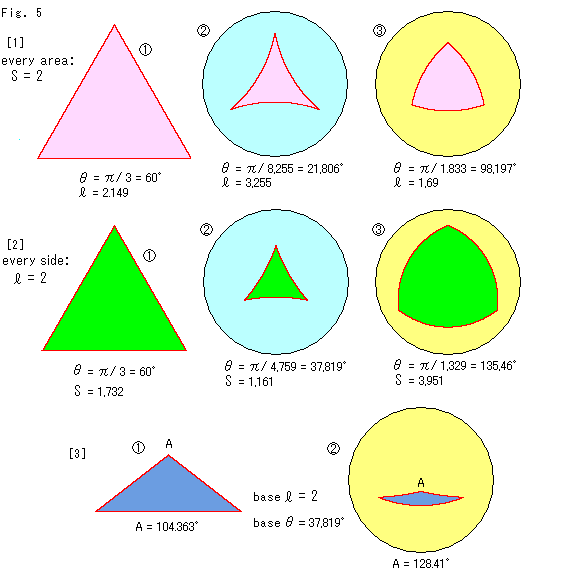
Look at Fig. 5.
[1]: We let the area S of regular triangle be 2.
: The regular triangle is drawn in Euclidean geometry.
: The hyperbolic regular triangle with the same area S is drawn on Poincare disk.
: The elliptic regular triangle with area S is drawn on our disk model of elliptic geometry.
The caluculation of area is done by above fomulae (1) and (2). 
is the internal angle of triangle. The triangle is a regular triangle so that A + B +C = 3. All internal angles are just as we see by our own eyes. That is, each triangle has its typical angles though the area equals to other triangles. 
is the length of side. In elliptic geometry the length of side is Euclidean length on the corresponded great circle on the sphere. Euclidean triangle looks very large but the area S of each triangle is exactly equivalent to others.
[2]: This time, let the length of side be 2.
Then, the appearaces of triangles are shown as , and . Of course, all length of sides are equal though their appearace is very different.
[3]: Let us see isosceles triangles for a reference. Angle-Side-Angle is a rule used in Euclideangeometry to prove triangles are congruent. Let two angles be 37.819
is the same as that of in [2]. Similarly let the length of base between the two angles be 2. is Euclidean triangle, and is the triangle that has the same Angle-Side-Angle on our disk model of elliptic geometry. The internal angle of the upper vertex is not identical each other.
By the way, let think about "the same thing" widely. The area does not change in [1]. If we pay attention only to that, we can say three try angles are the same. In [2] the length of side does not change. Similarly, if we pay attention only to that, we can say three try angles are the same, too. But we can not say that they are congruent.
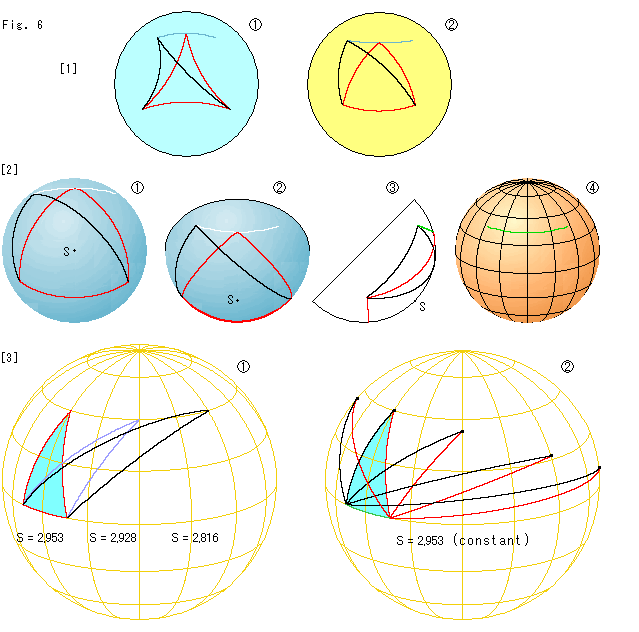
Look at Fig. 6.
Now we make equivalent deformation of the triangle on our disk model of elliptic geometry, and compare it with that of hyperbolic triangle. We fix the base and move the upper vertex in the same way of Fig. 2.
[1]: Poincare disk and our disk model of elliptic geometry are put side by side.
: The green line is the locus of upper vertex when the vertex is moved while keepin the srea constant like the black tip. The shape of locus is curved like 
.
: The area of triangle is the same as that of Poincare disk. This time, the shape of locus is oppositely curved like 
.
When we line the two disk models,
We can easily guess that the character of plane in hyperbolic geometry is quite contrary to that of elliptic geometry.
But we can not judge what kind of curve the locus is only by seeing .
[2]: To see it let us observe the equivalent deformation on the hemisphere that is the origin of our disk of elliptic geometry.
: It is the view from the south pole S (bottom) of the hemisphere. The white line is the locus. It looks like instead of because of the hemisphere. The triangle on the sphere is much bigger than the triangle on the disk because the disk size is made uniform with hypebolic one. Though the triangle on the sphere looks a similar figure to that of the disk, it is not true.
: The south pole is shifted down. Naturally the locus looks like . Though the locus looks like or , it shall be the curve in of [1].
: It is the left side view of the openwork of .
: We took out only the locus and put it on an exatra sphere with longitude and latitude. Its earthfs axis is arranged just for our observation, not the same as or . Seeing this, the locus might be a latitude line.
[3]: Let us confirm it.
Fix the base on the equator as shown in . And we moved the upper vertex along a latitude line. The area S of triangle changes very slightly.
Then, we move the upper vertex while keeping the area S invariably as shown in . The sky blue triangle is set as the standard. The locus, needless to draw, has nothing to do with a latitude line. The entire sphere is not necessary for our disk model, so that we drew triangles on the
hemisphere (our side of the two halves).
Suppose we forget about projection and use the sphere entirely, it is possible to extend the movable vertex going arond the sphere. But when the vertex arrives at the opposite longitude of the sky blue triangle, the vertex falls to the equator and we can not draw any triangle.
Similarly to Fig.2 that is in hyperbolic geometry, the locus is not parallel to the green base. It is natural because there is originally no parallel plines in elliptic geometry. The locus is not an equidistant line like a latitude. Not a straight line (great circle) either. It is not a small circle that can be made by cutting a sphere with a plane, either.
We have tried to image up hyperbolic geometry by comparison with elliptic geometry in equivalent deformation. We want to find something like Riemann's sphere in hyperbolic geometry, don't we? There must be similar idea, we guess.