There are several kinds of models for the Hyperbolic Non-Euclidean World, such as Poincare's disk, Klein's disk, the hemisphere model, the upper half plane, the hyperboloid model, the dual graph, Beltrami's Pseudo-sphere, and so on. But only the two disk models show the entire world. Here we look at the two disk models, Poincare's and Klein's, and the hyperboloid model in connection with the two disk models.
The radius of a disk model depends on what is called curvature or metric, but we choose to make it 1 in Euclidean measurement in order to keep things simple.
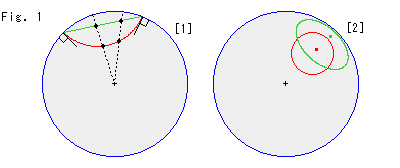
Look at Fig. 1.
Both types of disks, Poincare's and Klein's, are superimposed on each other. On Poincare's disk model, a straight line looks like a circular arc (red) that is perpendicular to the disk edge (circumference at infinity). But on Klein's disk, a straight line is straight (green).
[1]:The red and green curves are the same hyperbolic straight line. The points on these lines correspond to each other as shown.
[2]: Hyperbolic circles have a hyperbolic radius 1. Their centers are located at a hyperbolic distance of 1.5 from the origin. A circle is drawn as a circle (red) on Poincare's disk, but as an ellipse (green) on Klein's disk. As you can see, both centers are not at the visual centers of the circle or the ellipse.
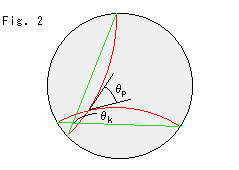
Look at Fig. 2.
Angles 
and 
are hyperbolically the same. On Poincare's disk is just as it looks. But on Klein's disk we have to compute or convert the green lines to red lines (Poincare's).
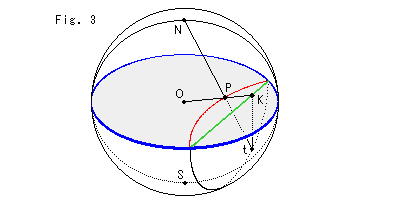
Fig. 3 shows the relation between Poincare's disk and Klein's disk. Point O is the common center of the sphere and the disk with blue edge. The disk is used for both Poincare's and Klein's models. Point P is on Poincare's model and point K is on Klein's, and they correspond each other. Point N is the north pole and point S is the south pole, supposing that the disk is an equatorial plane. Point t is on the southern hemisphere, and the straight line tK is vertical. That is, points N, O, P, K and t are coplanar.
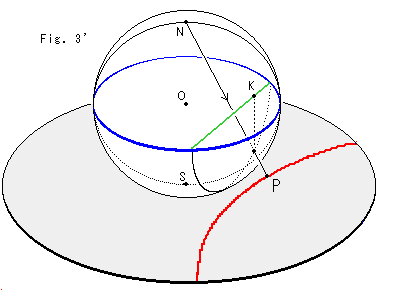
Fig. 3' shows a simple way to get Poincare's model without going up and down. It directly changes a straight line to an arc. But the diameter of disk is twice as big as the above one, so we have to observe it accordingly.
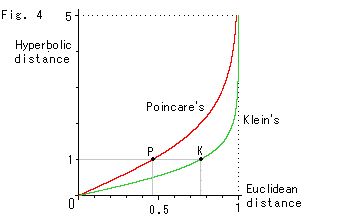
Fig. 4 shows distances from the origin on Poincare's disk and Klein's disk. Points P and K in this figure correspond to those of Fig. 3. Within about 0.5 hyperbolic distance, the ratio of visual distances in the two disks is roughly 1 to 2.
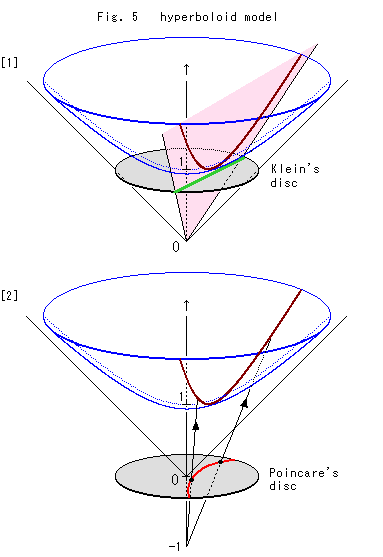
Fig. 5 is a hyperboloid model. It represents the surface of revolution of a rectangular hyperbola. The bottom of the hyperboloid is at distance 1 from the origin O. Though the model is actually stretched up to infinity, it is cut for easy observation.
[1]: A hyperbolic straight line (brown) on the hyperboloid is the line of intersection with a plane (pink) that goes through the origin O. We put a disk on the bottom of the hyperboloid, which allows us to get the corresponding straight line (green) on Klein's disk as the line of intersection with the plane.
[2]: Also we put a disk at the origin O, and make a sweeping ray from the point -1 on the axis of revolution to the brown straight line on the hyperboloid as shown. Then we can get the corresponding straight line (red arc) on Poincare's disk.
We have called this hyperboloid a model, but, needless to say, it is not a model unless we have the agreement or definition (metric) of distance for the model. However, there is a revolution model called Beltrami's pseudosphere, which requires us only to regard the shortest distance (geodesic) as a straight line. Later on, we will look at it.
[Note]
Hereafter, the following terms will refer to those in the Hyperbolic Non-Euclidean World unless specified:
straight line, circle, parallel,
length or distance, area,
angle, right angle, perpendicular, etc.
There are several ways to convert one model to the other. But let's leave them and go to see various matters.