
We live on the earth, and we know it is a sphere. But how do we know it? We cannot confirm it with our own eyes unless we fly up into the universe by spaceship, instead we watch a space trip on TV or we look at a globe or a map and we feel as if it is actually so. Similarly we want to see such views in the Hyperbolic Non-Euclidean World with our own eyes by fair means or foul, even if the actual object is invisible.
A map is useful. Fig. 1 is a Mercator's projection. To draw the giant earth on a sheet of paper, we first consider that the earth is shrunk. Points on the earth are projected to the paper and rolled around. However, scaling the earth down is not so simple. The scale changes when you get further from the equator. To the north and south, a reduced scale gets bigger. So we cannot draw a map at a very high latitude. There, the Mercator map is quite distorted. And yet it is very useful because we know the distortion.
Mercator's true map is based on a so-called conformal mapping. So, Fig. 1 is incorrect. But here we use it for the sake of simplicity. We will see accurate Mercator's map in chapter 21.
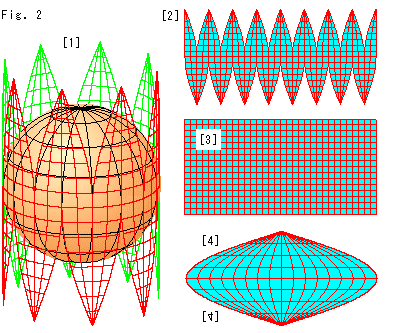
Look at Fig. 2.
This time, we make a sphere to a plane just like peeling an orange. It includes the north and south poles.
[1]: The sphere is cut and cylindrically opened. For easy observation the truncated cylinder is drawn in skeleton with different colors, the front is red and the back green. The cylinder surface gets distorted when the sphere changes into the cylinder but the length of latitude (horizontal line) and the intervals of longitude (meridian) are preserved. (Half amount of longitude and latitude on the sphere is omitted.)
[2]: The cylinder of [1] is unrolled flat. You may have seen a world map of this type.
[3]: Each of upper and lower lobe of [2] is stretched to right and left, and tears are mended. The frame is rectangular but the ratio of length to breadth is exactly 1:2 differing from Mercator's. And latitudes are drawn at regular intervals. The upper end line corresponds to the North Pole and the lower end to the South Pole. That is, both upper and lower edges are lines that were originally points and expanded to straight lines.
[4]: The upper and lower lobes of [2] are, contrarily to [3], gathered and filled the gaps. The number of longitude and latitude is reduced in half to make it easy to see. You may have seen this type of world map, too. The longitudes are sinusoids (sine-curves). And each area surrounded with longitude and latitude equals to that of the sphere. But the length and angle are evidently not equal to those of the sphere.
We can say that a map is 100 percent correct if we measure it based on the defined rule. The rule is called metric. It shows a difference from Pythagorean theorem. There are many kinds of world map in Internet.
What is the map of the Hyperbolic Non-Euclidean World? It is called a model and is visible for us who live in Euclidean world. The model is usually drawn on a plane. It is distorted also, but unluckily there is no hyperbolic terrestrial globe or similar thing can help our understanding. The distortion or metric is described only in numerical formulae, hyperbolic trigonometry, etc. Well, it's funny that an actual object should be found when we have a map and metric. Yes, that's right. However, it is impossible to draw the object visually. Why?
We cannot see the outward appearance of the Hyperbolic Non-Euclidean World or hyperbolic space from its outside just like that we cannot look down our universe from the exterior. But we may guess that the shape of the hyperbolic space is a sphere since the character (geometry) of the hyperbolic space is the same everywhere, which is what is called homogeneous. The hyperbolic space is also isotropic, and it looks the same in all directions. In other words, there is no preferred direction in hyperbolic space. However, a substantial object that we want to see is inside the mechanism of hyperbolic space, not its outward appearance.
At any rate, all discussions of the Hyperbolic Non-Euclidean World continue with models only. Therefore, let us see how models are made.

Look at Fig. 3.
There is a term curvature that is used to describe how an object is curved. The curvature of a sphere is positive, and the curvature of a plane is zero. A hyperbolic plane (space) has a negative curvature, which is the opposite to that of a sphere. Usually we take 1, 0 and -1 for elliptic geometry, Euclidean geometry and hyperbolic geometry respectively.
The hyperbolic plane is, of course. But, as a result, it becomes like a saddle at every point if we measure a length on the plane in the ordinary way. Fig. 3 shows this condition. Remember this does not mean that the hyperbolic plane itself is curved. Then, what kind of rules should we make to treat a plane as
a plane? This is what we are about to investigate.
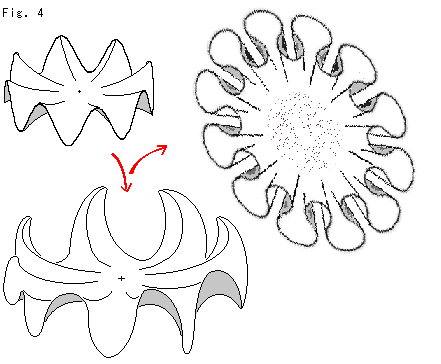
Look at Fig. 4.
The saddle of Fig. 3 is a situation very near around (neighborhood) a point. Now let it occupy the region wider a little. It flares and corrugates. Here please imagine that it freely extends without interference in other parts. But what we have to get is a flat surface that includes the entire hyperbolic plane. (There are photos of some knitting that shows this type of plane on the Internet.)
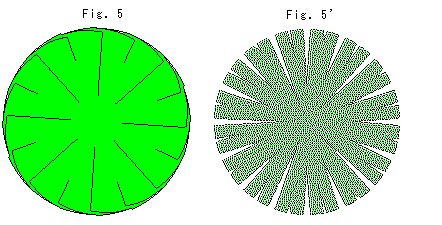
Now, we first press it down and make it flat as shown in Fig. 5. This will cause it to develop many wrinkles. The edge is still finite in area but wrinkles develop more and more.
On the contrary, if we press a globe which is like an egg keeping constant surface area (not rubber made), it will burst open like Fig. 5'. The hyperbolic plane is thoroughly opposite of it.
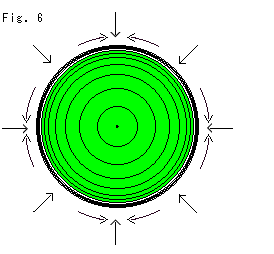
Next, Look at Fig. 6. We compress the plane with gathers in the direction of the circumference, say ironing. And simultaneously we compress the plane in all directions of radiation in order to draw infinity into the model. We can do this by shrinking our ruler (log graduation). Then the wrinkles will
disappear, and we get a perfect flat disk with a finite radius. (Don't ask us if it is possible to pull in the infinity. Please forget it for the time being.)
Thus we get a beautiful disk model that is completely flat in Euclidean finite size. Concentric circles show equal intervals of hyperbolic distance from the origin. They are for a Poincare's disk model. The intervals will be about double if we make a so-called Klein's disk model.
We have to use metric that fits for a model we chose. When we do so, we get true hyperbolic lengths and angles. At the moment every point becomes a saddle in the Euclidean sense.
Now this Poincare's disk model theoretically represents the actual hyperbolic plane.
Let's look at it in a diagram;
Surprisingly there is a Euclidean curved surface in the shape of saddle at every point. It is called Beltrami's pseudo-sphere. We will see it later.
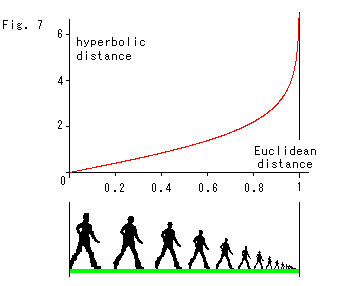
Look at Fig. 7.
The red curve is the relation between hyperbolic distance in Poincare's disk (radius = 1) and Euclidean distance that we, observers can see.
The circular edge of disk is drawn. But residents in the model cannot get to the edge no matter where they go. The edge is infinity for them. We, with the model in hands, observe that they shrink themselves as they walk to the edge. Measures also shrink as they walk. But actually their size never change and they can walk endlessly in the same step. Nothing blocks their way. Such a situation is named open. So is the model is open.
Oppositely when we say closed, we can arrive at a certain point but never beyond it.
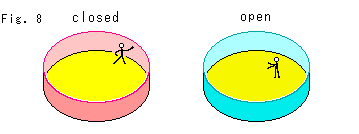
Look at Fig. 8.
Let us illustrate "open" and "closed".
The red domain is closed. A man in this domain is allowed to walk around and touch the boundary (wall). But he cannot go out of the boundary.
The sky blue domain is open. A man in this domain is free to walk around but never to touch the boundary.
In algebraic expression they are
b can be infinity ![]() . In case of open with b =
. In case of open with b =![]() , we can give a any number however large except infinity
, we can give a any number however large except infinity ![]() that is b.
that is b.
Let us pay attention. The hyperbolic space has no boundary for the people in it. To draw the boundary of infinity (circumference) is only for us who are watching a model.
In daily wording "open" means that we are free to go in and out, and "closed" means that we can neither go in nor go out. In mathematics, however, we cannot go out of a domain whether it is closed or open. In either case, it makes sense if the outside world exists.
[Note] The term "model":
There are two kinds of models. One is the identical to the actual object in theory, 100 percent. The other is an illustration that partially represents the actual object in a way of thinking. For example, Fig. 4 is the latter. So we should be careful to distinguish which is the case.