Once you get into the Hyperbolic Non-Euclidean World, you may feel crazy and perplexed by the strangeness of it all. In the Hyperbolic Non-Euclidean World, it is well known that parallel lines meet each other. And rumor has it, among other things that:
"There is an infinitely large triangle with an interior angle of zero.",
"No ordinary regular square can be drawn.",
"There is congruence but no similarity.",
"The area of a triangle is determined by its interior angles only.",
"Distance and angle depend on each other.".
If the Hyperbolic Non-Euclidean World is so strange, we should try hard to take a good, concrete look at it. Let's start by looking at triangles and inscribed angles.
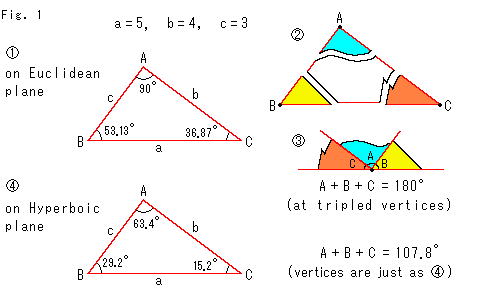
Look at Fig. 1.
Let us see how crazy triangles in the Hyperbolic Non-Euclidean World are.
: It shows a triangle on the Euclidean plane.
: We tear off vertices A, B and C.
: And just like making children consent, we gather them as shown. Three viertices are at the point on a straight line. It proves the sum of interior angles is exactly 180
.
: We bring the triangles into the Hyperbolic Non-Euclidean World. You may go there with a ruler. What is called length depends on the character of world where it belongs. However, both an object and a ruler change togather at a time. Namely length does not change. If it is allowable idea, we can draw the same figure in both worlds.
Suppose a triangle that has the same side in length as is on hyperbolic plane now. We measured the interior angles of the triangle and found that every interior angle is smaller than that of . Accordingly the sum of them is smaller than 180. It is what we have heard.
However, if we do like , the sum of interior angles becomes 180. But we must pay attention to that three vertices are laid down at a single point. It means that there is not a side nor gap between vertices. Angles A, B and C in are not identical with those of due to the fact that length and angle depend on each other. It is natural that we get 180 by doing . Therefore on hyperbolic plane no trangle is tearable and no vertex is movable.
To tell the truth, the interior angles of are calculated by using hyperbolic trigonometry. We can not draw a plane with such a mechanism. So we left the plane as it was, and we changed the way of measurement (calculation formulae). They often say "It is the hyperbolic world if the sum of intrior agles of a triange is less than 180". It is measured with ordinary ruler and protractor. It agrees with what calculated by hyperbolic trigonometry. That is the true hyperbolic plane.
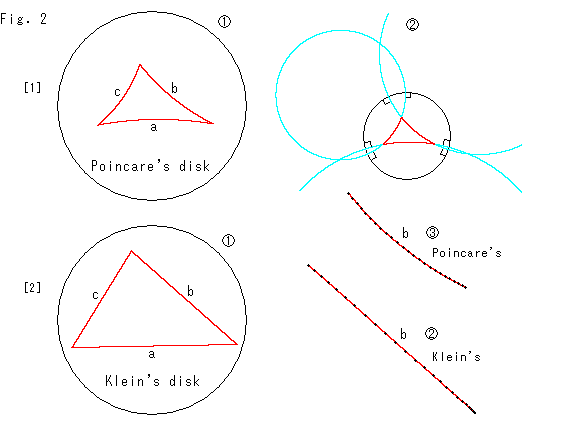
Look at Fig. 2.
There are models that covers the entire plane in the Hyperbolic non-Euclidean World. One is called Poincare's disk and the other one is Klein's disk. They are kind of an accurate map. The disk edge is infinity viewing from the inside. However, it has not fixed grid like longitude nor latitude. Because such an indication changes by location and so we can not draw it in the disk.
[1]: It is Poincare disk. We drew the triangles in Fig. 1. It can be done any place inside the diske. But for easy view, we set the gravity center of the triangles at the disk center.
: Every side of the triangle is a circular arc.
: The side is a part of a circle that crosses the circumference of disk perpendiculally. The angle viewed by our own eyes is the same as an actual hyperbolic angle.
: Side b is spotted at regular interval of hyperbolic length. It is enlarged for easy to see. The gap of spots gets shorter as they go to the end point.
[2]: We drew the same triangle in Klein disk.
: This time, edges of the triangle is straight. In Klein disk a straight line is drawn as a straight line.
: Side b is spotted similarly to that of Poincare's.
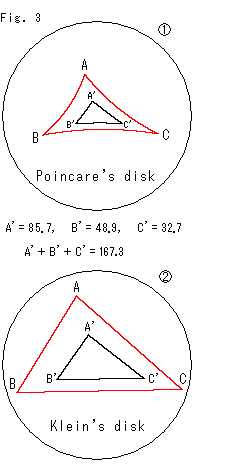
Look at Fig. 3.
We draw a small black triangle A'B'C' in the original red triangle ABC. The former size in sides is 1/3 of the latter. Their garavity center are common.
: It is Poincare disk. The interior angles of small triangle A'B'C' are bigger than those of the big triangle ABC. That is to say, there is no similality in hyperbolic plane. Compare it with in Fig. 1. The smaller a triangle is the closer the sum of interior angles gets to 180.
: Similarly we draw the big and small triangles on Klein disk. These triangles may look similar to our eyes. But it is not true. Angle on Klein disk should be calculated with length of sides.
Suppose a figure is enlaged n times. In Euclidean geometry we can not recognize it if a ruler also is enlarged n times. In hyperbolic geometry, however, we immediately notice the difference between the original figure and enlaged one. See the difference in angles. We feel that something like absolute length exists.
When we come full circle, we get back to the originalpoint. Angle 40 or 50 or whatever has geometrical meanig. On the other hand what is called length has no such basis. The unit length can freely defined. In hyperbolic geometry, however, it seems that there is an abusolute unit length because angle and length depend on each other. We will see it later.
In middle school, you learned that "The inscribed angle is constant." Yes, this has been proven. However, no one has explained to us why this is so. My elementary school teacher told us, "The circle ratio (the ratio of the circumference of a circle to its diameter) is 3.14". But, why do both a big circle and a small circle have the same 3.14 ratio? She did not give us a reason. A proof shows only the rightness of a statement, but not why it is so.
Some people say that it is a natural property. Others say that it is a characteristic of Euclidean geometry itself. We had felt that they were good at making excuses.
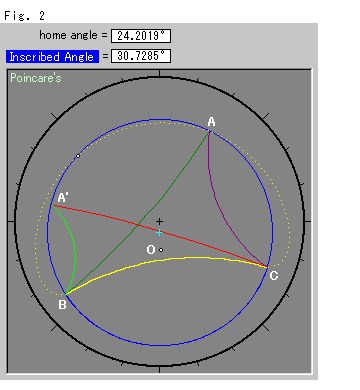
Look at Fig. 2.
It is Poincare's disk model. In this disk:
A hyperbolic straight line is visually a circular
arc which is perpendicular to the model disk edge.
An angle of intersection of two straight lines is
the angle of that of circular arcs.
A hyperbolic circle is drawn as a circle, but its
center becomes lopsided toward the outer edge of
the black circle.
Do you think it is reasonable?
Well, let's examine it and follow what the authorities say even if you are not quite satisfied with their explanation. This is essential. Besides, isn't easier to complain about something after seeing it?
The center (origin) of the model disk is marked black "+". The blue loop is a hyperbolic circle. The white spot O is the hyperbolic center of the blue circle. The sky blue "+" is the visual center of the blue circle. Notice that the center O is somewhat apart from the visual center. A triangle ABC is on the circle as shown in the figure. The yellow side BC is fixed, but the vertex A is movable along the blue circle. For an example of this we can move A to A' in the figure. In the Hyperbolic Non-Euclidean World, the inscribed angle changes from the original (home) angle BAC when vertex A moves, as shown in the upper portion of the picture.
The yellow dotted loop is the locus of vertex A. When we force it to move without changing the home angle at A, the locus is no longer a circle, nor an ellipse. Therefore, in the Hyperbolic Non-Euclidean World:
It is easy to guess this conclusion after reading about it in a book, but have you ever seen it visually? Now you have. Visualization is one of our aims, which is why we drew it.
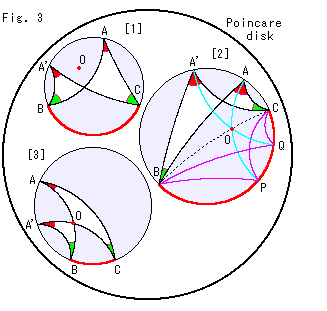
Look at Fig. 3.
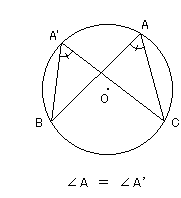
Let's draw circles inside Poincare's disk and observe inscribed angles. The sizes of three circles in the disk look different but all circles are hyperbolically congruent. The red spot O in each circle is its hyperbolic center.
[1]: On the circumference there is a point A' that has the same inscribed angle as that of given point A. In this case, the green angles B and B' are
also equal.
[2]: The red arc BC is a semicircle and the dotted straight line BC is a
diameter. Similarly to [1], point A' has the same inscribed angle as that of given point A. This time, we also find other two points P and Q like point A'.
Points P and Q are located opposite to point A and A' but any inscribed angle of them is not supplement to others in 180 as in Euclidean geometry. Let's draw hyperbolic straight lines among points, A to P and A' to Q as shown with sky blue lines. These straight lines intersect at the center O. Namely lines AP and A'Q are diameters. Points A and P are symmetric to each other with respect to the diameter BC. So are points A' and Q.
[3]: Let's draw a straight line from the one of end points B of red arc BC passing the center O, and get the point A on the circumference. Point A has an inscribed angle A. Similarly, we draw a straight line from point C to point A' through the center O. The inscribed angles A and A' for red arc BC are equal. That is to say, straight line A'C shall pass the center O if straight line AB passes the center O.
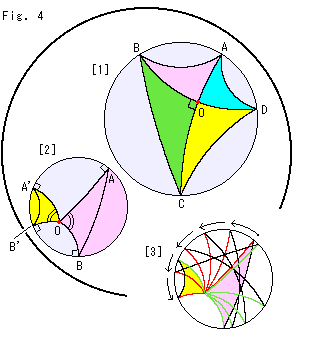
Look at Fig. 4. Let us draw some more. The size of circles are the same as above.
[1]: Let's draw two diameters AC and BD. They intersect orthogonally at the
center O. All interior angles of quadrilateral ABCD are the same. But quadrilateral ABCD is neither a square nor a rectangle. In hyperbolic geometry we can never get a quadrilateral with four right angles. Every interior angle is divided exactly in two by diameter (diagonal) AC or BD. The colored triangles are congruent since all radii are identical. In hyperbolic geometry triangles are identical if their corresponding inteior angles are the same no matter what they look like in the disk model. And similar to Euclidean geometry, the base angles of an isosceles triangle are equal.
[2]: The center O the of circle is a common point to the pink sector and yellow sector. A triangle is drawn in each sector as shown. Every side of the sectors is perpendicular to the circumference. Both the sectors and the triangles are congruent to each other. The length of an arc on the circumference can be decided only by the radius and central angle, just like Euclidean geometry.
[3]: In this circle we see the rotation of the pink sector of [2]. The pink sector will visually be smaller and exactly be superposed to the yellow sector. If we turn the yellow one, it will visually get bigger and exactly be superposed to the pink sector.
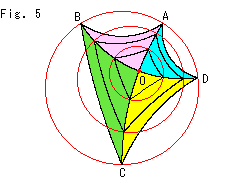
Fig. 5 shows a situation when we shrink the circle of [1] in Fig. 4. The quadrilateral ABCD is getting smaller, and closer to an ordinary square. Therefore, we cannot change the size of a figure while keeping its angles. In the Hyperbolic Non-Euclidean World there exists no similarity. However, a triangle is a triangle and a quadrilateral is a quadrilateral no matter whether we enlarge or shrink it.
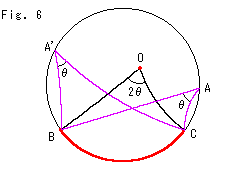
Fig. 6 is a picture we drew to see if an inscribed angle is one half of a central like Euclidean geometry. The answer is what we already learned above. Only specific points A and A' meet it. That is, there is no theorem like that in hyperbolic geometry.
Now we have learned that the inscribed angle is not constant but rather it changes. Then, what is the Hyperbolic Non-Euclidean World as an entire space? In this case it is useful to investigate, individually, the differences between Euclidean geometry and hyperbolic geometry. But first, we want to know the Hyperbolic Non-Euclidean World globally. So let's see how the disk model is made.