In the previous chapter, we saw what straight lines are in the Elliptical Non-Euclidean World. Here we will take a look at triangles.
In the Elliptical Non-Euclidean World, when we move a triangle far towards infinity, what will happen?
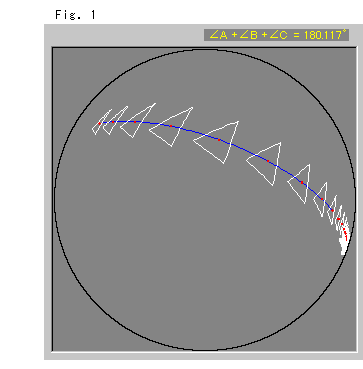
Fig. 1 shows what happens when we move a triangle at regular intervals on a straight line. The blue line is the locus of the center of gravity (the red spot) of the triangle. Visually, the triangle appears to get smaller and smaller as it moves along the line, but actually no change in size. The sum of the interior angles of a triangle is accurately calculated as shown in the yellow equation at the top right of Fig. 1. It is greater than 
. We use ordinary spherical geometry for this calculation.
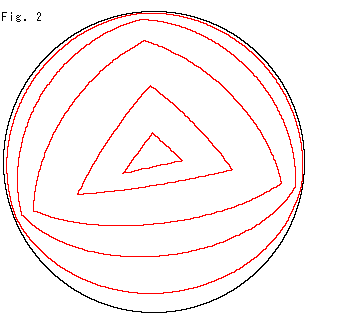
Fig. 2 shows triangles changed in size. We clearly see that the sum of the interior angles is greater than , and it gets bigger as the triangle gets bigger. But the maximum is 3, when the triangle is as large as the edge (circle) of hemisphere model.
When we use the hemisphere model with a radius of 1, the area S of a triangle with interior angles A, B and C is:
The maximum value of the area S is 2. That is the full area of the hemisphere.
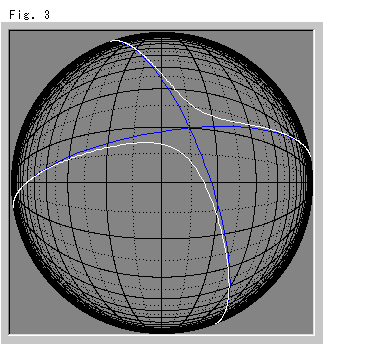
Fig. 3 is a hyperbola we drew incidentally. It looks strange shape, isn't it? The blue line are asymptotes. The both ends of the white hyperbola may possible be connected behind the sphere-like disk.
A true model of elliptic geometry must be on condition that;
The shape of model is a sphere (radius 1).
A great circle on a sphere is regarded as a straight line.
A length is Euclidean distance on the sphere.
The length of a straight line is finite and its maximum value is 
.
A angle is the Euclidean angle of intersection of two great circles.
Antipodal points are identified.
Figures we have drawn do not meet this condition. First, there is no infinity in this condition. In addition, the shape of this model is a overall sphere. Well, it is inconvenient for us, isn't it?
Anyway, let us go to the Hyperbolic Non-Euclidean World, Part 
. We will try to construct a better model when we compare with hyperbolic geometry.