The formula of parallel angle is

The right side can be rewritten by using symbol C, which is a combination of k and e.

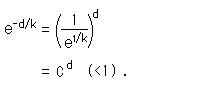
Here we see what will happen if k, e or C are changed. When k is big enough in comparison with distance d, or when e gets close to 1, the right side of the parallel angle formula approaches 1, and the parallel angle will be almost a right angle /2.

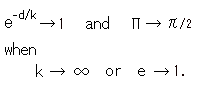
When k is small enough in comparison with distance d, or when e is very big, the right side approaches 0, and the parallel angle will also be almost 0.

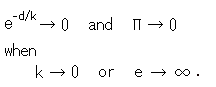
And by using parameter C,

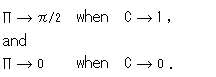
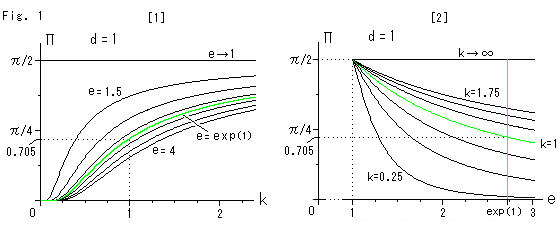
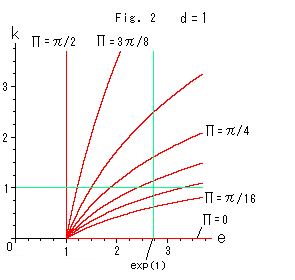
Fig. 1 above shows relations among k, e and parallel angle when d is fixed at 1. [1] is relations between k and parallel angle at every e. [2] is relations between e and parallel angle at every k.
Fig. 2 left shows relations between k and e at everyparallel angle when d is fixed at 1.
Fig. 3 below is 3-D graphs showing the combination of Fig. 1 and 2. The two figures are the same viewed from different direction

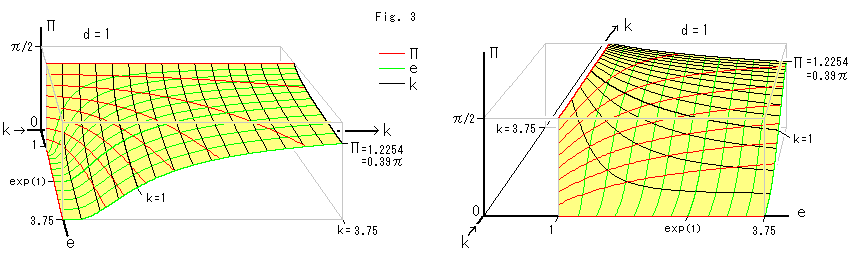
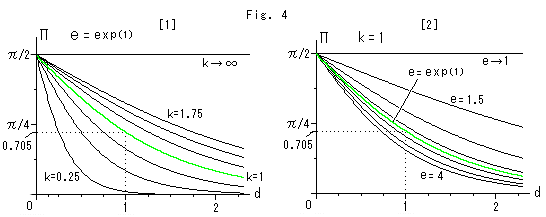
      Fig. 4 below is relations between d and parallel angle . e is fixed in [1] and k is fixed in [2].

      Let us combine k and e into new symbol C. The formula (1) of parallel angle can be rewritten by using C as

What will happen when C changes? The movable area of C is  0 < C < 1 .

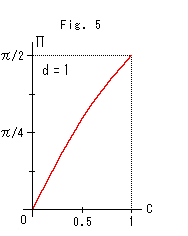
      Fig. 5 shows how parallel angle dpends on C. is almost in proportion to C, isn't it?

      Fig. 6 below shows k and e when C is chosen.

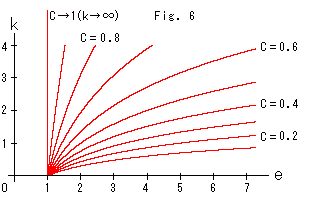
      Thus we have seen relations among k, e and parallel angle . At this moment, we cannot help but say "that's all" though we learned how they work. However, we feel that they may have some connection with what is called curvature or metric. We will se later on.