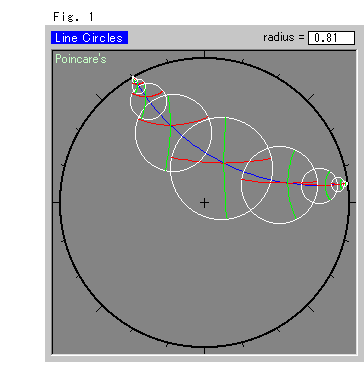
In the Hyperbolic Non-Euclidean world, when we move a circle, what happens? The circle itself never changes simply by moving it, but it changes visually on a model quite a lot.
Look at Fig. 1 carefully.
The blue line is a straight line. The picture is the trace of a moving circle along the blue line. The red and green lines are diameters and are perpendicular to each other. Their intersection is the hyperbolic center of
circle. The red diameter is intentionally drawn horizontally at the center. The circles are drawn at regular intervals.
The further the circle moves from the origin, the more the center slips toward the model's edge, and the circle appears to shrink.
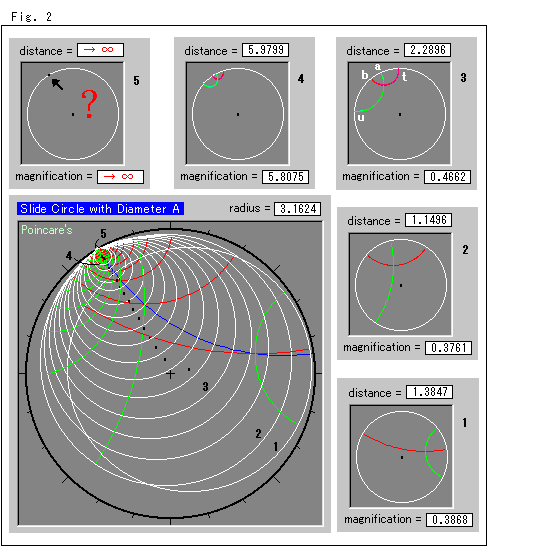
Look at Fig. 2.
This figure makes it easy to see how diameters look. Snapshots of a moving circle are shown in the small picture windows. The distance shown in each picture is a hyperbolic distance from the origin, and the magnification in the small picture windows is for your visual convenience. The magnification is the ratio of the visual size (which is a circle in the small picture window) to a corresponding circle in the big picture window. However, we do not know any situation when the whole circle goes to infinity. So we marked it "?". The interval between the circles on the blue line are not constant but are provided just for our observation. The black spots are the visual centers of each circle.
See upper right picture 3. The length of the white arc ab (the visually shorter side) equals the length of the white arc tu (the visually longer side).
And they have the same central angle of ![]() /2 seeing from the hyperbolic center.
/2 seeing from the hyperbolic center.
In small picture 4, right above, the red and green diameters look very small. But they are still actual diameters.
These visual matters result from the character of the model disk. We will see more about this later.
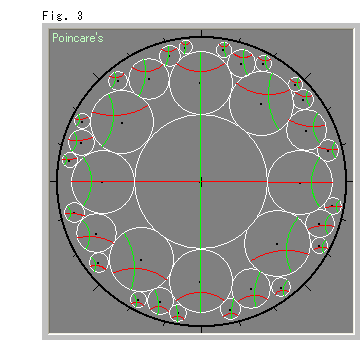
Look at Fig. 3 right.
Mr. A in the hyperbolic plane looks his neighborhood at various locations. The figure shows his own view drawn in our Poincare disk. While circles with radius 1 are his neighborhood. All the circles are congruent, of course. The four points of the compass for him never change wherever he goes.
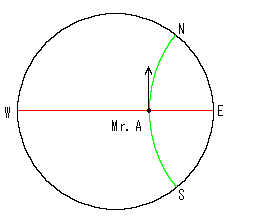
The direction may look different between his foot and neighborhood. But it is not true. N-direction for Mr. A is straight up as shown with the arrow. It is similarly to south, east and west. That is to say, it is the same as our surroundings. You may suppose that a ray of light comes along the green curve from point N to to Mr. A.
As to length, however, it is very different from ours. For instance, the length of a circumference with hyperbolic radius 1 is 1.1752 (= sinh 1) times as long as 2![]() .
.