Ch. 21 Horocircle 3, Pseudo-sphere 2 
By changing the way of expansion of the Upper Half-plane 
, we will see what a horocircle is like, and also we will make Beltrami's pseudosphere.
Look at Fig. 1. The red circle is a horocircle. The top of it is at the intersection O' of the gray base line (Y = 1) and Y-axis, and the bottom is at the origin O. We drag the horocircle along X-axis with a fixed point at point O'. Sky blue circles are dragged horocircles.
Fig. 1' shows the picture that we expanded and contracted Fig. 1 for actual hyperbolic length. In the X-directions area above the gray base line is compressed and area below the gray base line is expanded. In the Y-direction area above the gray base line is compressed down and area below the gray base line is infinitely expanded downward.
And now, the red horocircle is torn up right and left, and sky blue horocircles are drifted to the right.
To see how horocircles look like at infinity below, we re-scaled the area under the base line by using that of the model. That is, we pushed up infinity. Fig. 2 shows it. Arrows indicate the direction to push up. We changed color of the lower part of sky blue horocircles to white because of irregular scale. The black dotted line is X-axis drawn irregularly.
To see right area of Fig. 2, we intentionally compressed the lower part in the X-direction by force as shown in Fig. 2'. See arrows. The black dotted curve is an infinite boundary pulled in from the right under the base line. Though white lines look gathered at point P, we guess that they do not touch the dotted curve even if they touch X-axis that is infinity below.
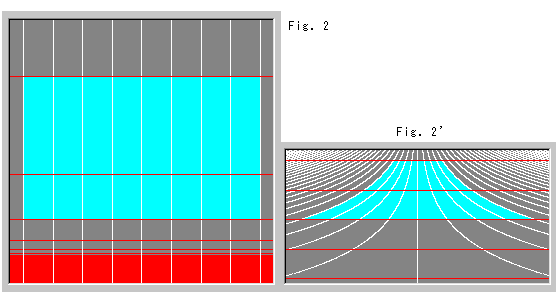
Fig. 3 shows the horocircle with infinite radius and the visual center has gone up to the upper infinity. The circumference of horocircle looks a straight line. White lines are odd-radii and are at regular intervals on the circumference.
Fig. 3' shows a picture that is a figure of Fig. 3 expanded and contracted for actual hyperbolic length. The upper side is cut for correspondence to that of Fig. 3. It looks every odd-radius goes up to a single point at infinity, doesn't it? And their curvature looks like the pseudosphere.
Fig. 4 above is to make Beltrami's pseudosphere by a cut-out of Fig. 3.
(1) is the cut-out in 2
width and infinite height above the base line (Y = 1). It is just for simplification that we sandwich Y-axis in the middle. In the cut-out color is thinner upward. It is intended to show area density on the Upper Half-plane .
(2) is a cylinder made by connecting both sides.
(3) shows that we are compressing the cylinder so that length on its surface becomes real hyperbolic length. As to the circumference all we have to do is to shrink it to actual hyperbolic length. But in the other direction, we have to press it down not only in the axis-direction but also in the sloped direction. Because the surface is not parallel with the axis. The red line indicates that we compressed the cylinder only in the circumference-direction and axis-direction like Fig. 3'. We depress the deformed cylinder some more.
(4) is the pseudosphere we made.
In this procedure we first made a cylinder. It is to make a smooth joint at the skirt by right angle to right angle. However, we may compress the cut-out first without rolling.
Look at Fig. 5.
(1): We compress the cut-out lengthwise and widthwise, and then we slice it like light blue horizontal lines and get numberless segments.
(2): We make them rings. And we pile up the rings with a center-axis.
Then we get the pseudosphere that is the same as (4) in Fig. 4 after the piling is completed.
When we apply either way, it is not necessary for us to rely on the Upper Half-plane . All we have to do is that we shrink the cylinder appropriately or that we make accurate rings and pile up them correctly. But we cut-out the Upper Half-plane in order to see relations between the pseudosphere and the Upper Half-plane . And the cut-out was a part of the horocircle so that we could see relations among three, the horocircle, the pseudosphere, and the Upper Half-plane .
If we cut-out the Upper Half-plane more widely, we will get a layered pseudosphere. (The rings will be coiled.)
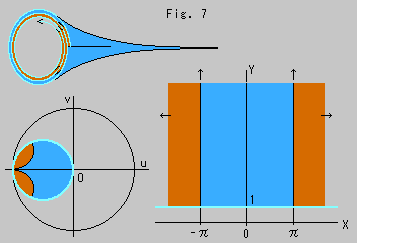
Fig. 6 shows situations in the Upper Half-plane , the horocircle on Poincare's disc model and a layered pseudosphere. Brown areas show the cut-out portion larger than 2 width. The sky blue base line in the Upper Half-plane corresponds to the circumference of horocircle and the edge of pseudosphere. Naturally we understand that the sky blue base line in the Upper Half-plane is not a straight line but extends to the same location of infinity from right and left.
Back: Ch. 20 Horocircle 2
Next: Ch. 22 Curved Space (Riemann, Metric, Curvature)
Table of Contents
Index