Metric is inconvenient to show peculiarity of the Hyperbolic Non-Euclidean World because every model has its own metric. It makes us feel that metric or weight has been intentionally applied.
We can tell right away whether a world is the Hyperbolic Non-Euclidean World or not if we know about curvature. Curvature is quite convenient because it is simply a constant value, while metric is described with an expression. Curvature here is what is called "Gaussian curvature".
By curvature, we are referring to the degree of curve. There are three types of worlds with constant curvature everywhere. The first is the Euclidean World, which has zero curvature. The second is the Elliptic Non-Euclidean World, which has positive curvature. The third is the Hyperbolic Non-Euclidean World, which has negative curvature. We usually adopt +1 as positive curvature and -1 as negative curvature for easy calculation. (Later, we will try to change the value of constant curvature.)
When curvature is constant, the degree of curving or distortion is the same everywhere. It is said to be homogeneous. In a space with constant curvature we can move a figure wherever without changing its length nor angle (isometric transformation).
It was Beltrami who first said, "Whatever has negative curvature has hyperbolic geometry."
In Chapter 18 we saw that the surface of Beltrami's pseudosphere is the Hyperbolic Non-Euclidean World. So the pseudosphere should have a curvature of -1. Here we will see if this is true.
Physically, Poincare's and Klein's disks are disks, and the upper half-plane is a plane. So, in order to get curvature, we have to calculate it via metric or the like. Luckily, we can calculate the curvature of a pseudosphere as an ordinary surface. However, the calculation is rather complicated and requires differential geometry. I, the author, am often at a loss when it comes to knowing how to carry out such calculations. So we will use a easy-to-use tools called an osculating circle and osculating ball. Let's go step by step.
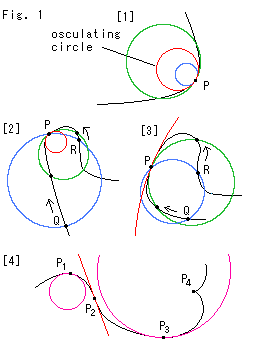
Look at Fig. 1.
[1]: It shows how we get an osculating circle at point P on a plane. Let the curve in the neighbourhood of point P be smooth and not twisted. An osculating circle is the circle that has the largest line-osculation (not point-osculation) with a curved line. That is to say, we regard a curved line as a chain of circular arcs with various radii, and an osculating circle is a circle that lies fully on one of the arcs at point P. It is the red circle in the diagram. The green circle is too large and the blue one is too small.
[2]: It is an accurate way to find an osculating circle at point P. We sandwich point P between two points Q and R on the curve. Three points P, Q and R define a circle. Now we move points Q and R toward point P. If the circle with the three points gets infinitely close to a certain circle, the latter circle is the osculating circle at point P. It is colored in red.
[3]: It is the same procedure as [2] but the circle with the three points P, Q and R gets bigger and bigger while they are moving toward point P.
[4]: Osculating circles at points 
, 
and 
on a curve. Point 
is an inflection point so that we cannot find "a certain circle". But, if we accept an osculating circle with infinite radius, the tangential line becomes an osculating circle. At point 
, the red osculating circle looks like it intersects the black curve. But we can define "a certain circle", and so we certainly get an osculating circle. At point 
, we cannot make an osculating circle because we find neither "a certain circle" nor a tangential line.
The curvature K at a point P where we can set the osculating circle with radius r is
If a line at a given point is straight or a point of inflection, then the radius of the osculating circle is infinity 
, and the curvature K at the point is zero.
We can get the curvature at a point on a curved surface with an osculating ball if the neighborhood around the point is in the shape of what is called spherical segment of one base. Such point is named umbilic. An osculating ball is based on the same idea as that of an osculating circle, and it is the ball that has the largest face-osculation (not line-osculation) with a hollow.
The curvature K at a point where we can set the osculating ball with radius r is
The curvature K of a sphere with a unit radius is, of course, K = 1 all round. If a surface at a point is not curved but flat, then the radius of the osculating ball is infinity , and the curvature K at the point is zero.
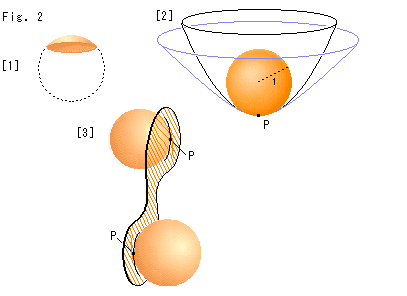
Look at Fig. 2.
[1]: It is a spherical segment. Every point on the spherical segment is umbilic.
[2]: An osculating ball is set in a paraboloid of revolution in a hyperboloid of revolution. In the case of the figure the osculating ball touches both surfaces of revolution at a common contact point P. The radius of the osculating ball is 1, making the curvature K of both surfaces K = 1. You might feel at a glance that the curvature of the hyperboloid is larger than that of the paraboloid. But it is not true because a curvature is what defind at a point. Since both surfaces are of revolution, we can also get their curvature by applying the method of Fig. 1 to one of their generators that passes through point P and squaring its result for a face.
[3]: It shows a concave-convex surface with osculating balls that are set in hollows.
By using two osculating circles let's measure the curvature of a surface excluding a spherical segment. Gaussian curvature K at point P is the product of the maximum and minimum curvatures of a curved line on a smooth plane that cuts the surface. Suppose the maximum curvature is 
and the minimum curvature is 
. Then the curvature K is
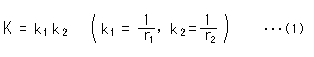
where 
and 
are the radii of osculating circles 
and 
respectively.
This formula is for the case where both of the osculating circles and are located on the same side in relation to point P. When point P is located between the two osculating circles and , we add a minus symbol "-" to the right side. Consequently, K < 0. The two planes on a generator, one is of maximum curvatue and the other is of minimum, always cut each other orthogonally.
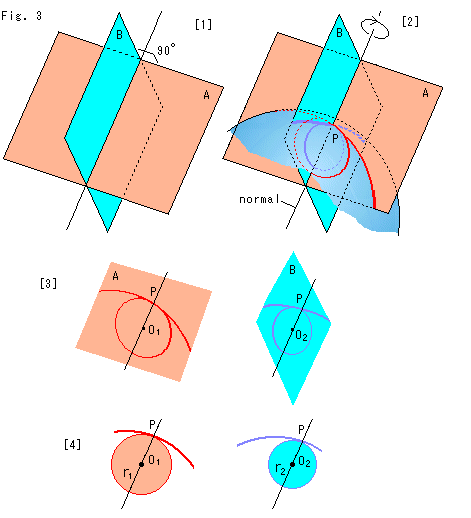
Look at Fig. 3.
We will find the maximum and minimum curvatures and using two osculating circles and .
[1]: First we fix two planes A and B to an axis. The two planes are at right angles to each other.
[2]: We stick the axis into a curved surface at point P as the normal. Plane A cuts the surface and gets the red curve on it, and plane B gets the blue curve on it. We set an osculating circle on the red curve and blue curve respectively. Now we rotate the two planes as shown in the illustration. Then the red and blue curves change, and, consequently, the sizes of their osculating circles also change.
One of the osculating circles may become infinity or the two osculating circles may exchange their position during the rotation, or we may not be able to get an osculating circle due to point-osculation. But that's OK. We will continue the rotation.
[3]: Let's denote the osculating circle on plane A as and the osculating circle on plane B as . The left figure is the maximum osculating circle with red curve. The right is the minimum osculating circle with the blue curve.
[4]: We turned pictures in [3] so that they face us. The radii of the osculating circles are and as shown. Now substitute them into formula (1) above. Then we get the curvature of the curved surface.
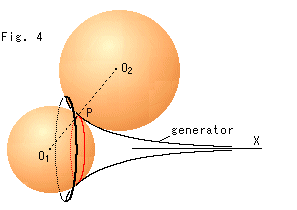
Look at Fig. 4.
Let's find the curvature of Beltrami's pseudosphere. The shape of the surface of pseudosphere is like a saddle. The figure shows when we put two balls, one is inside and the other is outside. However, these balls do not make face osculation. The inside ball touches the pseudosphere along the red circle as shown. The red circle is perpendicular to X-axis. The outer ball touches the pseudosphere along one of generators. Therefore, both balls are not osculating balls. However, in this case, we can get the curverture of pseudosphere. When we can put two balls (radius ) and (radius ) at a point, the curverture follows formula (1) with minus symbol.
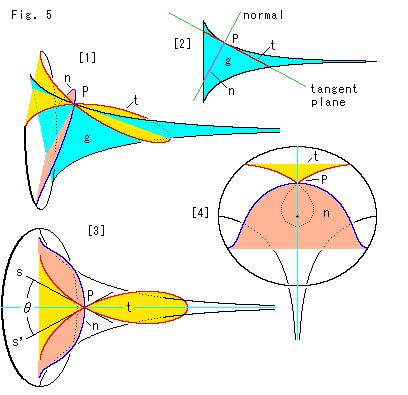
Look at Fig. 5.
Now let us think of a curverture with osculating circles, not balls. But an area for line-contact is limited.
[1]: Three planes g,n and t are cut-outs made with three planes that cut the pseudosphere at point P. These three planes are perpendicular to each other. Let us use the same symbols for cut-out lines and plances. The light blue plane g is surrounded with opposite generators. The yellow plane t is the tangent plane at point P. The line of intersection with plane g and brown plane n is the normal line that passes point P.
[2]: It is the side view of [1]. The red line is the cut-out t and the blue line is the cut-out n.
[3]: It is the view along the normal. Straight lines s and s' are tangent to the cut-out line t at point P. A circle that touches point P with the center on the normal must be located within angle 
, otherwise it can not make line osculation.
[4]: It is the view along the tangent line.
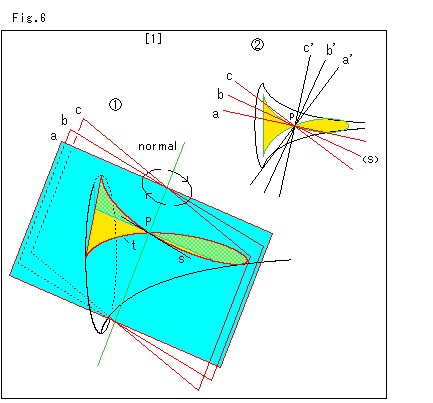
Look at Fig. 6.
Let us see a little more details.
[1]: We cut the pseudosphere with a plane that turns around the normal as shown with the arrow.
shows how we cut the pseudosphere. Only plane a is colored in light blue. The yellow area is the cut-out made by the tangent plane of pseudosphere at point P. The red curve t is its edge. The straight line s is the tangent line of curve t at point P. Planes b which is sandwiched between a and b cuts the pseudosphere along tangent s.
shows the view in the direction of normal. Planes a' , b' and c' are perpendicular to planes a, b and c respectively.
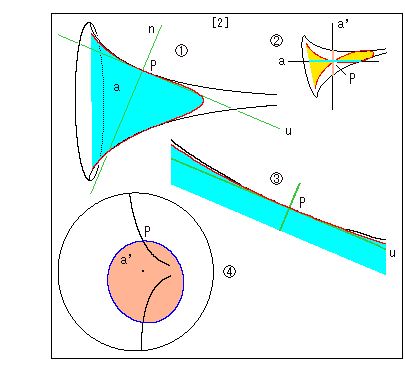
[2]: The relation with plane a and a' to the pseudosphere.
is the front view of the cut-out on plane a. Only the cut-out area is colored in light blue. The green straight lines n andu are the normal and the tangent respectively at point P.
is viewed in the direction of normal n. The light blue line is the cut-out made by plane a , and the brown line is the cut-out made by plane a' .
is an enlargement of near point P in . The red cut-out line is sunk at point P similarly to the generator, and we can see that it is over the green tangent on both right and left. Therefore, we can get an osculating circle at point P outside of the pseudosphere.
is the front view of the cut-out on plane a' . Only the cut-out area is colored in brown. We can get an osculating circle at point P inside of the pseudosphere. The black spot in the cut-out is the point where the axis of pseudosphere passes.
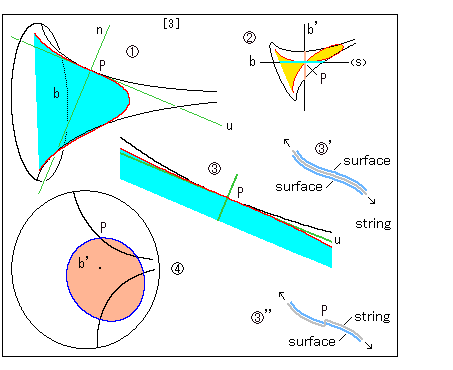
[3]: The relation with plane b and b' to the pseudosphere. It is drawn in the same manner as above.
In plane b passes tangent s.
In the left side of red line goes over tangent u and the right side goes under tangent u. That is, point P is an inflection point on the red line. We cannot get any osculating circle at point P on plane b.
We have drawn a straight line (geodesic) on the pseudosphere by using a computer. Here we want to see it on a physical pseudosphere by using a string rather than a computer. It is to feel what an inflection point is. However, the string must always contact with the surface of pseudosphere. To do so we need a little technique. We make a transparent pseudosphere. Its surface has some thickness though the true surface has no thickness.
' is a stratified pseudosphere that sandwitches a tretched string.
'' is a pseudosphere with an eyelet which a string passes through. If the string does not leave the surface when stretched in a certain direction, the eyelet is an inflection point on the string (straight line).
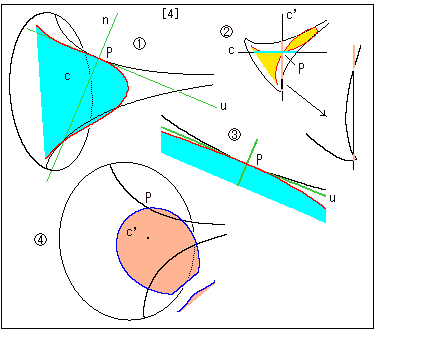
[4]: The relation with plane c and c' to the pseudosphere. This drawing is also made in the same manner as above.
In plane c' gets out of the pseudosphere once and grazes it at the skirt as shown with arrow.
In the red line goes down under tangent u on both sides of point P. So we cannot get any osculating circle at point P outside of the pseudosphere.
In the cut-out made by plane c' is broken near the skirt of pseudosphere.
Now we understand that the minimum osculating circle outside of the pseudosphere is only one that is on the plne that cuts the pseudosphere along the generator. However, we can no more information by drawings only.
Therefore let the outer osculating circle be the minimum one, and the inner be one right angled to the outer. And we go.
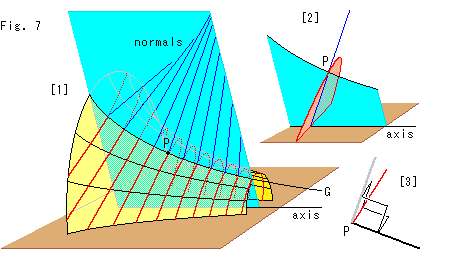
Look at Fig. 7.
[1]: The pseudosphere is laid on the brown plane that passes the axis. The light blue plane passes generator G and the axis. Normals on the genarator G are on the light blue plane. (Normals inside the pseudosphere are omitted.) Red curves are lines of intersection with the pseudosphere and the plane that is perpendicular to both generator G and the light blue plane.
[2]: Two cut-outs at point P are took out of [1].
[3]: The tangent lines of the two cut-outs and the normal line are perpendicular to each other as shown.
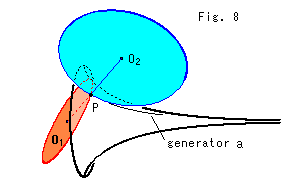
Look at Fig. 8.
Two osculating circles and sandwich the pseudosphere at point P. Straight line -P- is the normal.
We have to know radii of two osculating circles and to get curvature.
It is said that the curvature of pseudosphere is -1 wherever. But it is not easy for us to instantly agree because of its shape. Is it true?
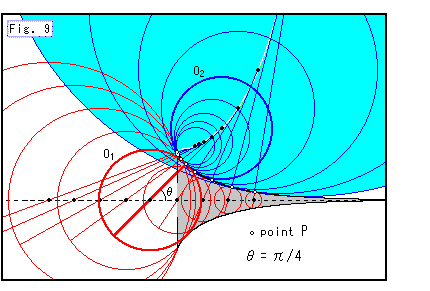
Fig. 9 shows the situation of two osculating circles and when the location of point P chages.
The red inner osculating circles are turned their faces to us for our observation. You may think that they are cross-sections of balls in Fig. 4.
When point P moves toward the tail, the curvature of a gerater gets looser, and the outer osculating circle becomes bigger and the inner osculating circle shrinks.
Radii of the two osculating circles and drawn thickly are exactly 1, and the angle of normal to the axis of pseudosphere is 45
.
When we move point P toward the skirt, outer osculating circle gets smaller and inner osculating circle becomes larger instead. But, at the skirt edge, no osculating circle is defined. If we take a limit value, the radius of osculating circle becomes infinity and the radius of osculating circle becomes zero. To apply formula (1), we make product of their curvature and . Then
Who understads it?
On the contrary, we are safe when we move point P toward the tail side. The radius of inner osculating circle gets smaller and smaller unlimitedly but never be zero. The radius of outer osculating circle gets bigger and bigger, but never be infinity. Because there is no tail end. It is open.
(The white locus of the center of outer osculating circle is called "catenary". We will take it up later.)
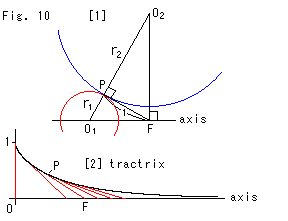
Look at Fig. 10.
Now we get the curvature K of pseudosphere. It is not necessary for us to know each radius of osculating circles and . What we need is the product of them. Since the curvature of pseudosphere is constant wherever, the product must be constant.
[1]: Let the foot of perpendicula from the center of be F as shown. Draw triangle F. And draw line FP. Then we get right angled triangles FP and FP.
Let radii of and be 
and 
respectively. Then
This result stands up wherever on the pseudosphere. The curvature K of pseudosphere is the reciprocal number of product with minus sign. That is, K = -1.
[2]: The black curve is the generator of pseudosphere. It is called a tractrix. Every red segment PF is on the tangent line of tractrix. The length PF is always 1 wherever point P is on the curve. From this drawing we can also understand that the curvature K of pseudosphere. (There is another smart way to find the curvature K. We will see it later.)
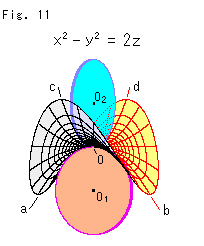
Let us see some examples of measuring curvature with oscalating circles based on our idea above.
Look at Fig. 11.
Osculating circles and are set at the origin of a saddle. Z-axis passes , O and . Curve ab along the valley is on Y-Z plane (x = 0), and curve cd along the ridge is on X-Z plane (y = 0)
Both osculating circles and passes the origin O so that we can easily compute their radii. We use Newtonian method. The radius r of curvature of a curve 
at the origin is
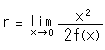
Both radii of and of the saddle are 1. Therefore the curvature K at the origin O of this saddle is K = -1.
Since the saddle is not the pseudosphere, curvature K depends on the point we measure. The surface of saddle is waved wherever and its curvature is negative regardless the distance from the origin O. However, the curvature gets rapidly close to zero when we leave the origin O a little. K = -0.1 at the edge.
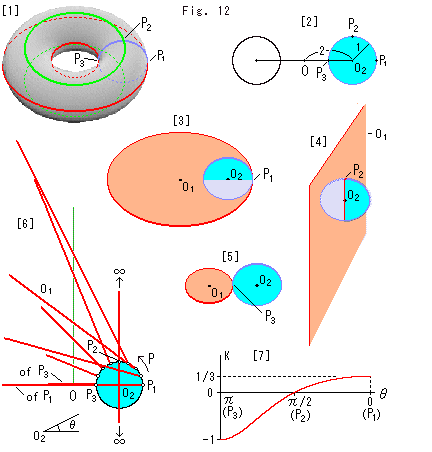
Look at Fig. 12.
[1]: The curved surface in the shape of a doughnut is called "a torus". The blue circle passes three points , and , and cuts the torus tube perpendicularly. The torus is not the earth but the blue line is called the meridian.
The red circle that passes point is the most outward circle on the torus. Let us call it the outermost ring.
The green circle that passes point is laid on the ridge of torus. The dotted green circle right under it is laid on the valley of torus.
Another red circle that passes point is the most inward circle on the torus. Let us call it the inmost ring.
[2]: It is the cross section of the torus cut vertically at the center O. The radius of tube is 1, and the radius of circle that passes the center of tube is 2. The radius of inmost ring is 1, and that of the outermost ring is 3. The light blue circle is osculating circle inside the tube.
[3]: Osculating circles and are set at point inside the tube. They are perpendicular to each other. The red osculating circle is the outermost ring. The curvature K of torus at point is K = 1/3.
[4]: The radius of red osculating circle is infinity so that the curvature K of torus at is K = 0.
[5]: Osculating circles and sandwich the torus at point . The red osculating circle is the inmost ring. The curvature K of torus at point is K = -1.
[6]: We set osculating circle in front of us, and move point P continuously from point to . Red osculating circles is drawn in its cross section (diameter). The green line is the locus of the center of . We haven't imagine the locus is a straight line. It's a surprise.
[7]: It shows how the value of the curvature K of torus changes when point P moves. When we move point P from point ( = 0), the curvature K get gradually smaller from 1/3. And it becomes zero at point . Then, it is -1 at point .
We have gotten curvatures, but how does the shape of curved surface change if its curvature changes? Why is it hyperbolic if curvature is -1? How does curvature concern in what angle and distance depend on each other? And how can we get the curvature of space? Space has usually no shape. We will see them by and by.