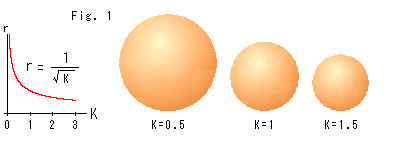
How does the pseudosphere change when its curvature changes? We can guess that an object with constant curvature everywhere changes only in size when the curvature changes, and we can guess that the object keeps its shape all the time. Let us confirm these guesses.
Fig. 1 shows the relationship between radius r and curvature K of a sphere. The sphere rapidly grows as curvature K gets smaller.
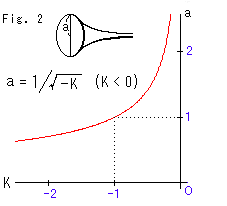
Fig. 2 shows radius a of the skirt of a pseudosphere for a given curvature K. The tractrix (generator of the pseudosphere) is
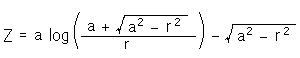
With this expression, it is not easy for us to feel that the pseudosphere changes only in size, is it?
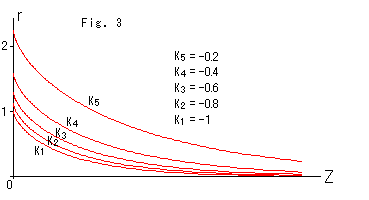
Fig. 3 shows how tractrix changes depending on curvature K. The pseudosphere rapidly gets bigger when we push curvature K to zero. (Accordingly the Euclidean size of a corresponding disk model rapidly gets bigger, too.)
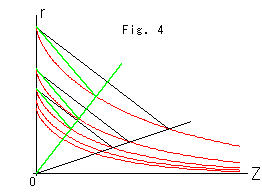
Fig. 4 is to confirm that the tractrix does not change in shape. Arbitrarily draw rays through origin O, and get similar triangles as shown. We understand that the shape of every curve is the same and so is that of the pseudosphere, regardless of curvature.
Curvature K in the Euclidean World is zero. What will happen if we let the curvature of a pseudosphere be zero? Does theurvature K infinitely get bigger without its shape changing? Yes, it does. And its surface is planar, too. The surface is now a Euclidean plane!
The radius of the corresponding disc model gets bigger infinitely, and the disc becomes a Euclidean plane.
Unless curvature K is exactly zero, the Hyperbolic Non-Euclidean World is purely as it is, namely hyperbolic, and the shape of a pseudosphere remains unchanged. Or let us say tghat the curvature K is always -1 if we use the radius r of skirt edge as a unit length. Therefore, it is quite all right to return to the normalization and fix curvature K as -1.