There is a clever technique for finding the curvature of a pseudosphere without using either differential geometry or osculating circles.
That is to apply what is called the Gauss-Bonnet Theorem:
Then we can immediately get curvature K from area A and Eular number 
(pronounced kai). The produt KA of curvature K and area A is called a total curvature. (Eular number is also called Eular's characteristic)
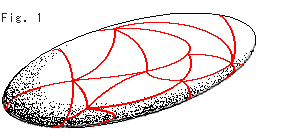
This formula is to be applied to a closed surface like a sphere or a torus. To obtain Euler number, we first cover the surface with triangles or squares. Fig. 1 is an exaple. Such covering is called cell-division or triangulation. And we count the number of vertices, edges and faces. A "vertex" is an intersection point of segments. An "edge" is a segment that conects between two vertices. A "face" is a surface surrounded with edges. "division" in cell-division does not mean to divide a surface but it is the result of the covering.
To get Euler number, it is not necessary to actually draw triangles or squares on a surface. All you have to do is to count numbers of vertices, edges and faces. Then
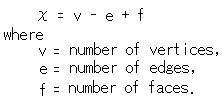
This formula is easy to memorize since 0-dimension (vertex), 1-dimension (edge) and 2-dimension (face) are in order.
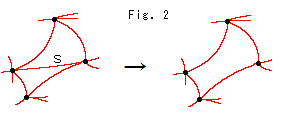
Look at Fig. 2.
We can eliminate edge s in this figure. Because the number of faces gets reduced by 1 when we take off one of edges, and Euler number remains unchanged. (Do not take off only a face. It makes a hole.) Triangles in Fig. 1 are too many.
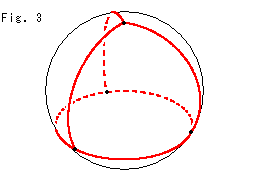
Look at Fig. 3.
Four triangles are enough for a surface that we can topologically regard as a sphere or a tetrahedron. Eular number is
= 4 - 6 + 4 = 2 .
Let the radius of sphere be r. Then curvature K is 1/
and area A is 4
. Therefore the total curvature KA of sphere is 4 regardless sphere size. Euler number that we get by substituting this KA to formula (1) is 2, which agrees the above.
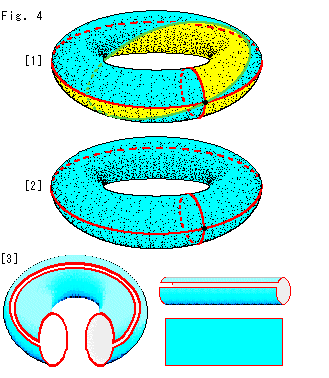
Look at Fig. 4.
How about a torus?
[1]: We can cover the torus with two triangles. Euler number is zero for
1 - 3 + 2 = 0.
[2]: We omitted an edge from [1] and cover the torus with a single face. We took off the green edge but you may eliminate the small red edge instead of the green edge because both go through the hole. Euler number in this case is also zers for
1 - 2 + 1 = 0.
[3]: We cut the torus of [2] along red edges, and open it as shown. Now we understand that the face is squre, and Euler number can be calculated as
0 - 1 + 1 = 0.
We will see the total curvature of torus shortly. As for cut-and-glue, we will see more in later chapers.
We know that the curvature K of the pseudosphere is -1. Now, let's find it by using the Gauss-Bonnet Formula... Wait a minute! We cannot make cell-division because the pseudosphere is not a closed surface and it has an infinitely long, sharpened tail called a cusp.
Luckily, however, there is a smart technique.
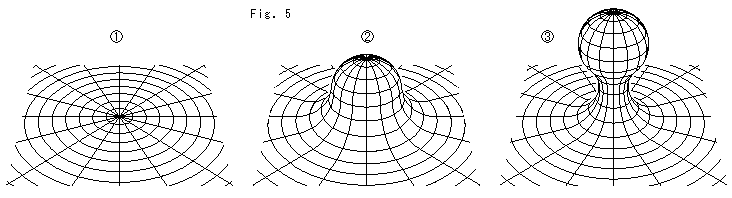
Look at Fig. 5.
We put a soft surface over an infinite large table. The surface is a plane 
if you do not touch it. We pushed up the plane from its bottom as shown 
. We can push it up more like 
. If we push down , it gets flatter to , and to plane again.
The curvature of plane surface is zero wherever. But the curvature on the deformed surface such as or varies point to point. And the total curvature is expressed with integration, and Gauss-Bonnet formula shall be
But don't worry about it. There is a fact that the total curvature of surface without boundary never change from the beginning no matter how the surface is deformed. We are free from hard integration when we apply this fact. If we blow up some area, the other area automatically grows narrower. But the deformation must be smooth. Iron out the wrinkles is out of quetion, though. Now new positive and negative curvature cancel totally. Therefore, the total curvatures of and are zero though they are not planes.
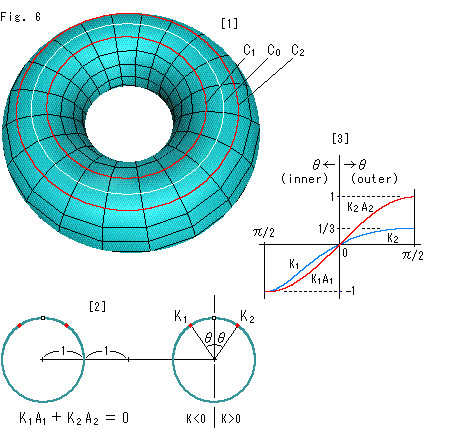
Look at Fig. 6.
A torus is a good example to see the cancelation of positive and negative curvature. We use a torus in good appearance for easy caluculation though the shape does not matter theoretically.
[1]: The white circle 
is on the top of tube. Two red circles 
and 
are located at the same distance from white circle . The pile of these circles forms the torus.
[2]: It is the cross section of torus. 
and 
are curvature at a point on circle and respectively. The product 
of curvature and the length (1-dimensional area) is the total curvature on circle . Similarly 
is the total curvature on on circle . And
stands up. This relation does not depend on the angle 
.
[3]: The blue curve shows the relatition amang angle , curvatures and at a point on the torus. It is -1 at the inner end and 1/3 at the outer end. The red curve shows the relatition amang angle , total curvatures , . (The red curve is vertically shrunk by 1/2 for drawing.) The red curve is symmetry in absolute value, which is different from the blue curve.
As can be seen from the above, the total curvature of (the entire) torus is zero due to the cancelation of positive curvature on the outer portion and negative curvature on the inner portion. The torus is not a deformed plane but curved from the beginning. Nevertheless, its curvature is zero. And we can get Euler number of zero from formula (1'). We did not use neither integration nor cell-division.
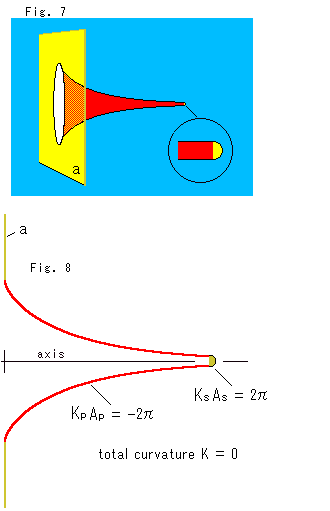
Look at Fig. 7.
Now let us get the curvature of pseudosphere. We imitate Fig. 5 but we do not deform the pseudosphere itself, of course.
First, cut off the tail at far away from the skirt of pseudosphere, where the radius is very small and almost constant. Cap the cut end with the yellow hemisphere as shown. Its enlargement is in the black circle. Next, we put the yellow plane a with a hole that fits the skirt.
The curvature 
of the yellow hemisphere with radius 
is 1/
, and its area 
is 2
. Therefore, the total curvature of the yellow hemisphere is 2, regardless its size. The area of the tail we cut off is very small though the length is infinitely long. So we regard the area 
of capped pseudosphere as 2 of the actual pseudosphere. Now we denote the curvature of pseudosphere by 
. Then we can spell 2 for the total curvature .
Look at Fig. 8.
It is a cross section of Fig.7, which is cut throgh the axis of the pseudosphere. The total curvature of the entire figure is zero based on the idea of Fig. 5. Therefore,
]] = 0 .
That is,
+ 2 = 0
Consequently we find that the total curvature of pseudosphere is = -1 . And also we get Euler number as = -1 .
Here please be noted.
This story is based on the previous information that the curvature of pseudosphere is constant wherever. We did not use formula (1) directly but we relied on only the idea that positive and negative curvature cancel. Also we got Euler number without using cell-division.
One more point. The end point of tail of the actual pseudosphere is open. The capped pseudosphere is not genuine. Nevertheless we got the exact curvature of the real pseudosphere.
By the way, do not plan to cover the skirt edge of pseudosphere with something like a hemisphere. If you do so, the capped pseudosphere becames a topological sphere.
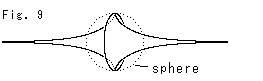
Fig. 9 shows a superimposition of a sphere and two identical pseudospheres. The area and volume (inside included) of the two pseudospheres is exactly equal to those of the dotted sphere. The area is 4
and the volume is 
, and they are in precise agreement. There might be some mechanism.