
Ch. 38 Projective Geometry (2) 
Let us continue to see projective geometry. We are going to see quadratic curves.
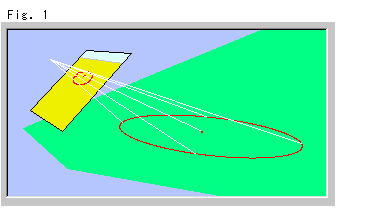
Fig. 1. is the projection of a circle on the ground.
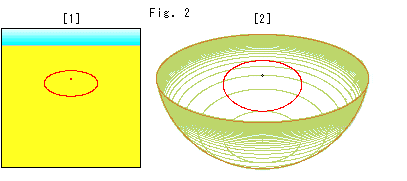
Look at Fig. 2.
[1] is the projected circle on Panel-screen. The circle on the ground is now an ellipse.
[2] is the projected circle on the hemisphere set on the ground.
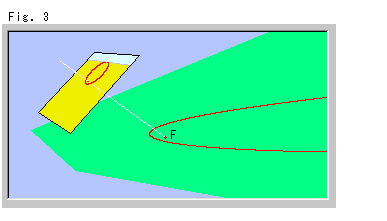
Fig. 3. is the projection of a parabola on the ground. The white ray is for the focus F only. (Others are omitted.)
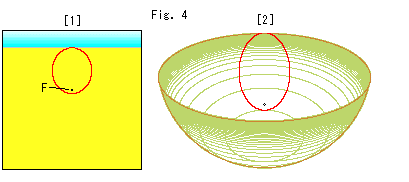
Look at Fig. 4.
[1] is the projected parabola on Panel-screen. It looks like an ellipse, too.
[2] shows the projected parabola on the hemisphere set on the ground.
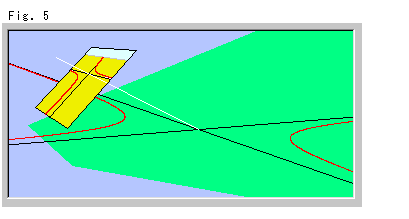
Fig. 5 is the projection of a hyperbola on the ground. Black straight lines are asymptotic lines.
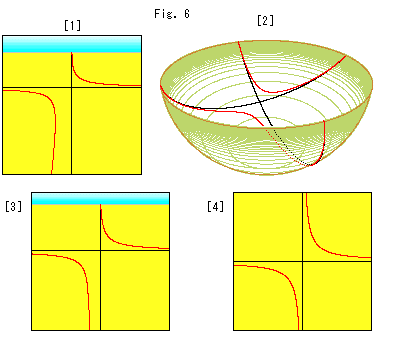
Look at Fig. 6.
[1] is the projected hyperbola on Panel-screen. One of branches of the hyperbola looks to meet with asymptote on the line at infinity. The bottom branch looks to leave the vertical asymptote. In a case of parallel lines, their gap looked getting wider as they went down, didn't they?
[2] is the projected hyperbola on the hemisphere set on the ground.
[3] is a picture on Panel-screen when the projection center (camera) gets to the right a bit in Fig. 4 aiming the center of hyperbola on the ground. The bottom branch does not leave but close to the vertical asymptote.
[4] is a picture when the projection center is placed right above the center of hyperbola on the ground. Naturally it shows an ordinary hyperbola.
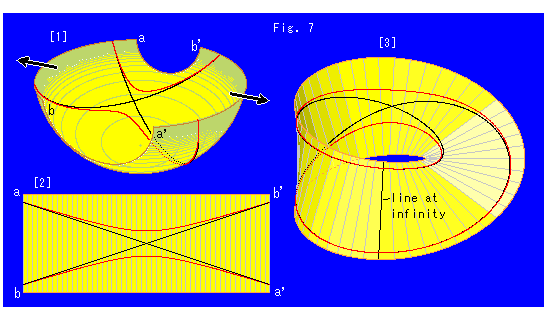
Fig. 7 above is to see a full range of a hyperbola placed on Mobius strip. A part of projective plane is Mobius strip.
[1]: Cut the hemisphere in Fig. 6 straightly down as shown.
[2]: Stretch it in the arrow direction by force, and make a belt.
[3]: Twist one end (right or left) of it half, and glue it to the other, a to a' and b to b'. Then we get a Mobius strip with the hyperbola that was in [1]. The jointed line is the straight line at infinity. The red hyperbola is a double-turnd loop now. Each asymptote forms a loop and meets with the hyperbola on the line at infinity.
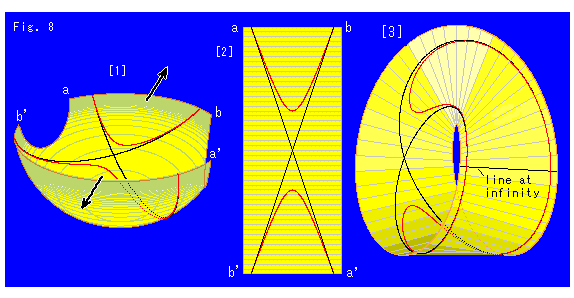
Fig. 8 is also to see full range of the hyperbola on Mobius strip. The hyperbola is the same as that of Fig. 7 but we cut the hemisphere in another way.
[1]: This time, we cut the hemisphere in another direction as shown.
[2]: Stretch it in the arrow direction by force, and make a belt.
[3]: Twist one end (top or bottom) of it half, just as we did before, and we get a Mobius strip. This time the red hyperbola is not a double-turnd loop but a single loop. It is because that Mobius strip is not the entire projective plane.
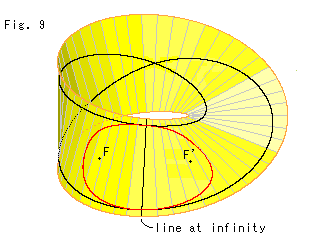
Fig. 9 shows a hyperbola with focal points F and F'. The focal distance from the center of hyperbola is made larger for easy to see the hyperbola entirely.
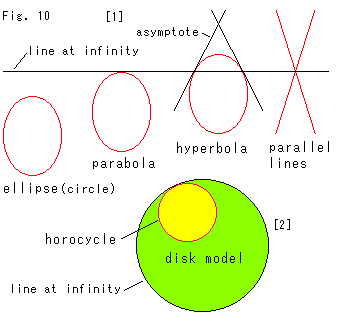
Look at Fig. 10.
[1] is a conceptional drawing to show the situation around the line at infinity. All kinds of quadratic curves on the projective plane is the same with exception that an ellipse (including a circle) never touches the line at infinity, that the parabola touches the line at infinity and that hyperbola intersects the line at infinity. The parallel lines get cross on the line at infinity.
Remember both areas (upper and lower region in the figure) of the line at infinity are finite area. We can go across the line at infinity but never beyond infinity. And the line at infinity is straight line though it is also the edge of hemisphere.
[2] is our guess on the way. The edge of disk model is nothing but the (man-made) line at infinity, isn't it? If so, it results that the situation of parabola drawn in [1] is the same as that of a horocycle. And we feel that the horocycle is a closed loop. However, we do not know whether the face of disk model is projective plane or not. Suppose the disk edge in Fig. 4 corresponds to the disk edge, we should identify antipodal points (end points of a diameter) of the disk. But it is unreasonable, isn'it? Also, in [1] we can go across the line at infinity but on the disk model we can't.
 Let us change our way of thinking a little.
Let us change our way of thinking a little.
Let parallel lines intersect themselves at given point P. And then the line at infinity passes point P. In other words we can freely draw the line at infinity anywhere, provided that parallel lines must intersect on the line at infinity. From this point of view, Fig. 10 looks regulations that quadratic curves and parallel lines must follow.
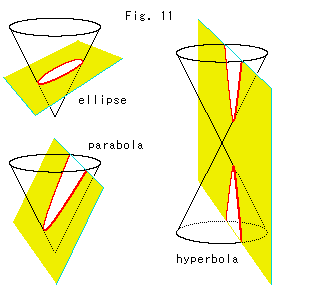
Fig. 11 is a popular drawing. We get all kinds of quadratic curves by cutting a conic with a plane. This suggests us that they are something to be unified. We may say [1] in Fig. 10 is the result. Well, honestly we have never imagined that the cutting-plane can be a one-sided surface. Wait. We have no evidence of such idea yet.
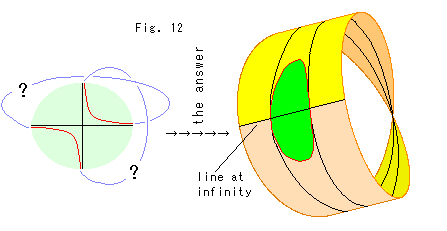
Fig. 12 is an illustration for the possible answer to the question what the head of branch of hyperbola is like. It is drawn by force. Of course, we do not insist the situation is like that. We may say that the twisted area beyond our view is mysterious zone. If we agree the identification of antipodal points of the hemisphere, we do not need Mobius strip. That is to say we should see the projective plane in mind.
[Back] [Next] [Contents]









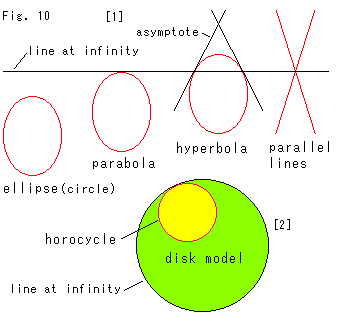
 Let us change our way of thinking a little.
Let us change our way of thinking a little.