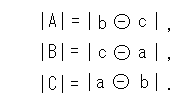Hyperbolic Non-Euclidean World
Ch.28 Pythagorean Theorem 
You know that the Pythagorean Theorem does not stand up in the Hyperbolic NonEuclidean World. This chapter is quite peculiar. It is based on Ungar's idea (the reference is at the bottom). It says that the Pythagorean Theorem is valid in the Hyperbolic NonEuclidean World if you appropriately change the definition of length and addition. Well, changing the definition will have secondary effect to, for instance, Parallel Angle. His theory does not say anything about such secondary effect. Nevertheless, he says that his idea is to be applicable to Einstein's relativity theory. Let us see what it is.
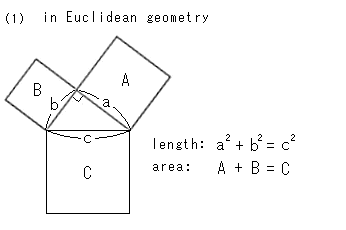
Figure (1) is the Pythagorean Theorem in the Euclidean World, which you learned at middle school. It consists of two formulae. One is relation of sides. The other one is relation of areas. However, in Euclidean geometry we do not distinguish one from the other bcause they are identical.
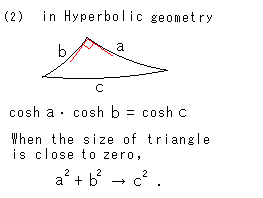
Figure (2) is so called Hyperbolic Pythagorean Theorem in the Hyperbolic NonEuclidean World.
It will be the same as ordinary Pythagorean Theorem when the size of hyperbolic right triangle is close to zero. It has no function of ordinary Pythagorean Theorem. First of all, there is no regular square in the Hyperbolic NonEuclidean World. Because the sum of interior angles is less than 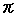 .
.
Now let us see the peculiar theorem. Hyperbolic distance d(a,b) between two points a and b on Gaussian plane (complex plane) of Poincare's disc model is normally
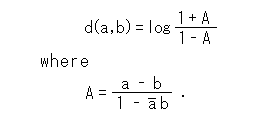
He changes this.
Use symbols  (Mobius addition) and
(Mobius addition) and  (Mobius subtraction). And define them as
(Mobius subtraction). And define them as

And distance d(a,b)

Similarly
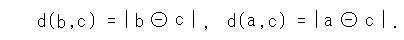
These satisfy trigonometric inequality

 This means that these distances meet with distance function inquiry.
This means that these distances meet with distance function inquiry.
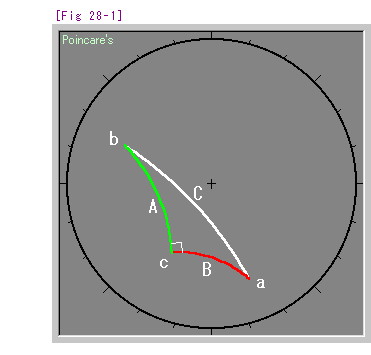
Look at [Fig 28-1]. Length of sides A,B,C of thiangle abc are
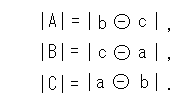
And relation among three sides is

This is Unger's Pythagorean Theorem in the Non-Euclidean World.
For proof, see Reference at the bottom of this chapter.
Also he says
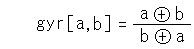
Gyro is the key word. brief introduction
We understand his technique. However, We feel it unfair to say "Pythagorean Theorem" because  do not mean area. Yet it is very interesting, isn't it?
do not mean area. Yet it is very interesting, isn't it?
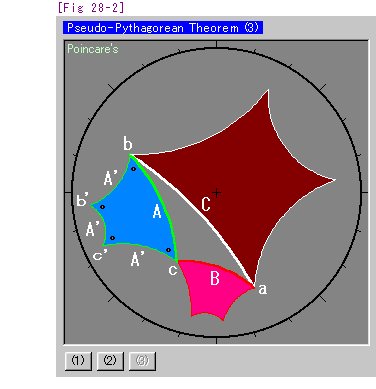
Out of habit, we drew a picture. That is [Fig 28-2]. Put Blue quadrilateral bb'c'c on side A, Red one on side B, and Brown one on side C. Four sides of every quadrilateral are equal. And four interior anales of every quadrilateral are equal. But any quadrilateral is not a regular square. So we name them pseudo-regular square for the time being.
On Blue pseudo-regular square,
|A'| = |A|, b = b'= c'= c .
Red and Brown pseudo-regular squares are similar to above.
Shape of these three pseudo-regular squares are different from each other. Because there is no similar figure in the Non-Euclidean World except congruent. We can not find any areal relation if we leave it just as it is. We feel that there might be some idea.
Reference:
Abraham A. Ungar;
(book) Beyond the Einstein Addition Law and its Gyroscopic Thomas Precession,
Kluwer Academic
(paper) Hyperbolic Pythagorean Theorem; Amer. Math. Monthly, Vol. 106 (1999), pp. 759-763
Next: Ch.29 Pseudo-sphere 4 (Gauss-Bonnet Formula)
Prev: Ch.27 Infinity 6 (Projective plane, Torus)
Table of Contents Index


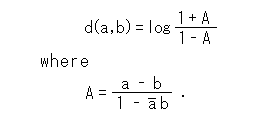

 This means that these distances meet with distance function inquiry.
This means that these distances meet with distance function inquiry.