In regard to the Elliptic Non-Euclidean World, we have a good tool at our disposal (cf. Chapter 1). However, we have never seen such a tool in the Hyperbolic Non-Euclidean World. Naturally, there is no way to make a correspondence between them. But let's try to compare one to the other visually. We are going to do it with a triangle.
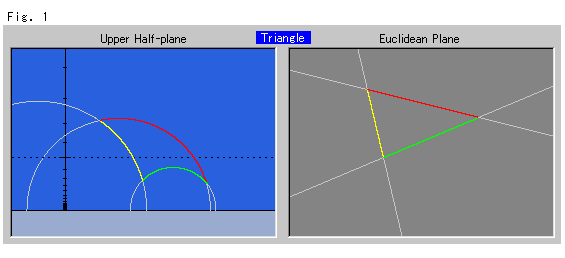
Look at Fig. 1.
The left blue plane is Poincare's upper half-plane 
. The right dull black plane is a Euclidean plane. Corresponding sides of the left triangle and the right are in the same color. The hyperbolic length in the upper half-plane and the length in the Euclidean plane are the identical.
The gray lines are for observation only. The black dotted line in the upper half-plane indicates the standard level of the Y-axis. The Y-axis is only for graduation, and its locations does not matter.
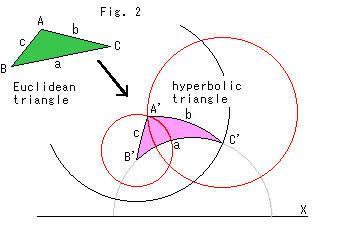
Fig. 2 shows an example of our construction for transforming a triangle in the Euclidean plane into a triangle in the upper half-plane.
Let us call a triangle in the upper half-plane a hyperbolic triangle and a triangle in the Euclidean plane a Euclidean triangle for short.
Green triangle ABC is a Euclidean triangle, and pink triangle A'B'C' is a hyperbolic triangle. Our rule of the reproduction is that we keep length unchanged in both worlds and we entrust angles to the regulation of each world. Because all angles are automatically settled in both world if we give lengths of three sides of a triangle.
The way of transforming a triangle is the same as we usually do with a pair of compasses in the Euclidean plane,
except that the center of a circle in the upper half-plane shits up.
First, we optionally draw a semicircle on X-axis for laying side B'C'. And we choose point B' on the semicircle. Then we draw two circles with the hyperbolic center B'. One is the red hyperbolic circle with hyperbolic radius A'B' and the other is the black hyperbolic circle with hyperbolic radius B'C'. Next, we draw another red hyperbolic circle centered at C' with hyperbolic radius A'C'. And we choose one of crosses of the two red circles as point A'. Then we get the pink hyperbolic triangle A'B'C' with hyperbolic segments as shown.
For the reverse transformation from the upper half-plane to the Euclidean plane, we just keep the length unchanged regardless angles.
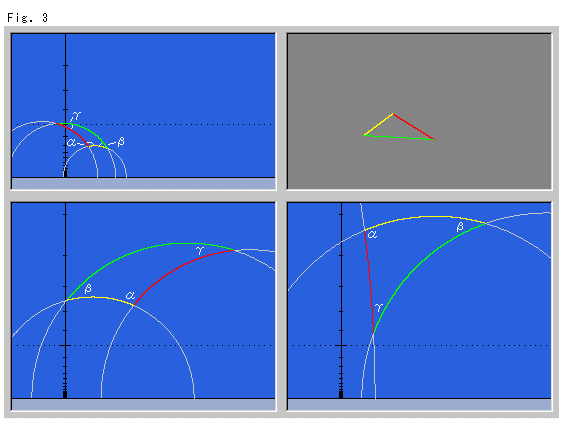
Look at Fig. 3 below. We choose points differently in the upper half-plane for one Euclidean triangle. All triangles are congruent though they visually look different. The interior angles of a hyperbolic triangle are smaller than those of a Euclidean triangle, but visually it is not so clear. This is because the Euclidean triangle is not big enough for observation.
Look at Fig. 4. We drew the Euclidean triangle slightly larger. We can clearly see the differences in the angles between Euclidean and hyperbolic triangles. Each interior angle of the hyperbolic triangle is obviously smaller than the corresponding angles of the Euclidean triangle.
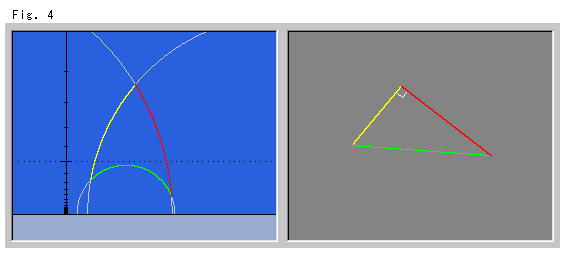
Fig. 5 shows a case in which one of the vertices is at infinity. The red and green half-lines in the Euclidean plane are parallel. It cannot be called a triangle. But in a hyperbolic plane, it is certainly a triangle. One of vertices reaches the X-axis.
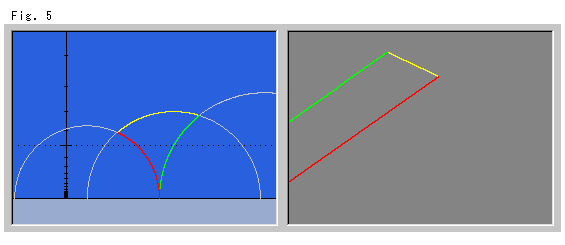
Now, we will look at parallel lines.
In the Hyperbolic Non-Euclidean World, there two parallel lines that pass a point (not on the base line). Parallel lines and equidistant lines are a completely different matter. So we will establish the following rules for our drawing. Let us call parallel lines in the upper half-plane "hyperbolic parallel lines", and parallel lines in Euclidean plane "Euclidean parallel lines" to keep things simple.
From hyperbolic parallel lines to Euclidean parallel lines:
The distance between Euclidean parallel lines is the distance from the base
line to the intersection of two hyperbolic parallel lines.
In a Euclidean plane, we draw parallel lines on either side of the base line.
From Euclidean parallel lines to hyperbolic parallel lines:
First, we take the distance between Euclidean parallel lines, and we draw
an equidistant line of the same length in the hyperbolic plane.
We optionally choose a point on the equidistant line and draw two
hyperbolic parallel lines that pass the point. (The two parallel lines and
the equidistant line intersect at this point.)
In any case we can set any inclination of Euclidean parallel lines. It has nothing to do with hyperbolic parallel lines.
Fig. 6 below shows the case where we drew hyperbolic parallel lines first. The yellow line is the base line. The white line is a bridge for observation only. In the hyperbolic plane, one end of the plane is at the intersection of the red and green hyperbolic parallel lines and the other end is perpendicular to the yellow base line. The length of this white line became the interval (distance) between the Euclidean parallel lines. The red and green dappled Euclidean parallel line is a double reproduction of both the red and green hyperbolic parallel lines.
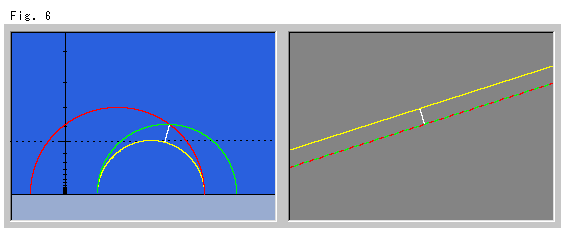
Fig. 7 shows the case where we drew Euclidean parallel lines first. The red and green dappled Euclidean parallel line is reproduced separately as red and green hyperbolic parallel lines. The black circular arcs are equidistant lines. They will form a full circle if either one of them is turned up or down. Naturally, we can select the lower equidistant line and any common point that hyperbolic parallel lines pass through.
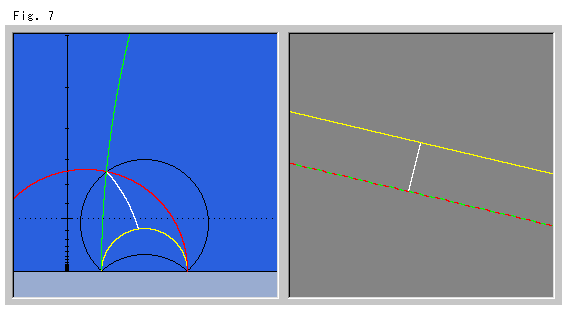
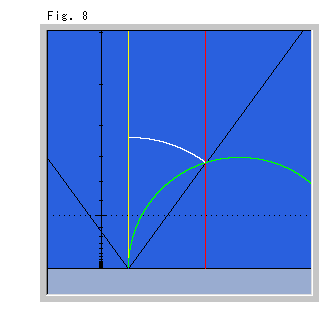
Fig. 8 right is also a case in which we drew the Euclidean parallel lines first, but the yellow base line is chosen as a line which goes straight up. (The Euclidean picture is omitted.) Equidistant lines are not circular but black V-style because they are stretched infinitely.
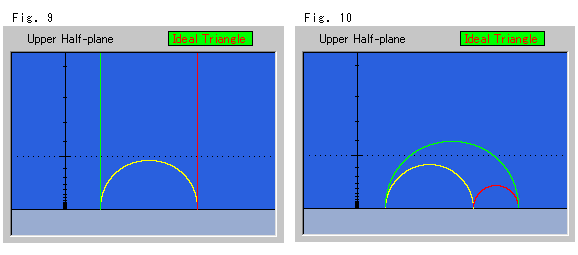
Look at Fig. 9 and Fig. 10 below. The red and green hyperbolic parallel lines intersect at infinity, and they form an ideal triangle with the yellow base line included. That is, the three of hyperbolic parallel lines are parallel and form a triangle at the same time. We cannot get a white line (a finite line) as we did in Fig. 6 through Fig. 8. Consequently, there is no visual connection between an ideal triangle and a Euclidean plane.
Thus, in this way, we are able to compare the Euclidean World and the Hyperbolic Non-Euclidean World with our own eyes, although there are some exceptions and optional matters.