Hyperbolic Non-Euclidean World
Ch.33 Revolution Eve (Topology) 
We have seen what the Hyperbolic NonEuclidean World is. That is a universally acknowledged truth if we accept the assumption of parallelism. We do not doubt it. However, there is a revolutionary idea.
They say that
hyperbolic geometry stands on things around us.
It is not necessary to regard the universe.
Needless to say, it is on topology. Let us see it.
To see it, however, we have to change our mind, and use a new approach.
Do you know the Euclidean geometry completely? We have been familiar with Euclidean postulates and their activities. As to the Hyperbolic geometry, we learned its postulates and trigonometry. But we have gained only a little experience in their activities. To know the Hyperbolic NonEuclidean World we should explore it more.
(This chapter is a preparation for the next chapter Figure-8 knot.)
* * * * * * * * * *
First we see what Euclidean geometry comes out.
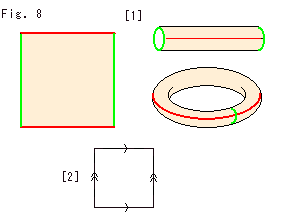
Here is a square. Suppose it is made of rubber. Make a cylinder and join the both ends without twisting as shown Fig. (1). Then we get a donut surface.
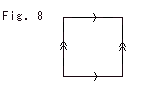
We mark arrows on edges of the square to indicate this gluing (identifying) method as shown Fig. (2). This square looks different from the donut surface, but they are topologically the same. In topology any surface is two-dimensional whatever it is deformed.
Here we call the square with arrow marks Square for short.
======================
We fictitiously imagine what abstractly glued without distorting Square. It is absolutely abstract so that we can not make any image. But we can think of or feel the abstract object.
It can be said that Square not only has the abstract gluing rule but also represents the abstract object in a sense. The representation is done by force though visualization is actually impossible.
The donut surface is what physically glued by force. "by force" means that Square is distorted.
The abstract object is essence. (This essence has no name.)
We will apply a way of thinking like these to subjects hereafter.
======================
A generic name for Square, the donut and the abstract glued object is 2-torus. "2" specifies two-dimensional. It is often called torus for short.
Since Euclidean geometry stands inside Square, it is said that
2-torus has Euclidean geometry.
You might feel strange but they also say that
the donut surface has Euclidean geometry.
You may deform this donut or replace with a coffee cup.
Let us count Euler number 
(cf. Ch.29). Torus has 1 vertex, 2 edges, and 1 face. Therefore,
= v - e + f
= 1 - 2 + 1 = 0 .
It is Euclidean if is zero.
Four corners of Square gather at a point (intersection of Green and Red lines) on the donut surface. Sum of four interior angles is exactly 2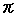
at the point without any gap or wrinkle.
On the donut surface we can make a circuit tour through or around the hole and get back to the start area. In Square, due to the identity of edges, you can never kick the right edge but your legs reappear from the left edge. When you hit a ball up, you can catch it at your feet. The square is finite domain without boundary.
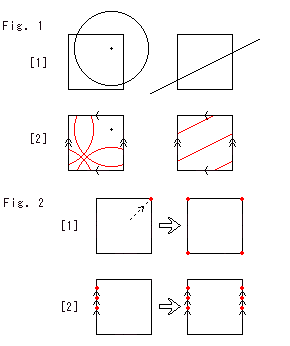
Fig. (3) shows a circle and a straight line on an ordinary square.
Fig. (3') shows the same movement as Fig. (3) but on Square.
Fig. (3') is a special case.
[a]: Four points (actually one point) simultaneously appear at four corners when a point touches a corner.
[b]: When a point moves on an edge as orbit, another point (actually the same point) moves on the opposite edge.
Fig. (4) is four-frame comic strip of a running knight on Square. He never disappear though he looks as if cut into pieces. Wherever he runs, he stays in Square.
Fig. (5) is a lattice with an agreement that any location is measured in each box. That is, infinite Squares are tiled. Then what we ordinarily draw a circle or a line expresses what drawn in a Square.
Fig. (6) is the same lattice as in Fig. (5) but based on different idea. A resident on the donut surface can not leave it because it is his whole world. In whichever direction he travels, he comes back where he left. That means, on the donut, he sees his own back. On the lattice identical men and matters are exist in ever box. Fig. (6) shows what he observes in his world. Now all 
moved simultaneously.
A box of the lattice is called fundamental domain.
* * * * * * * * * *
This time we think of a cube.
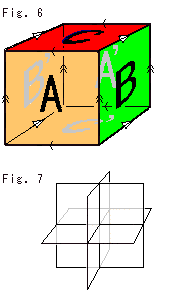This Cube is three-dimensional. "three-dimensional" means Cube has non-empty interior.
Look at Fig. (7). Direction of each face of this cube is indicated with four arrows on edges. A face is identified with that of opposite side. We call the cube with this gluing agreement Cube for short.
It is impossible to glue faces of Cube physically with the agreement. We have to do it abstractly. But do not guess it done in the four-dimensional world like SF novels. We must do it in three-dimensional space.
Do not guess that Cube becomes a visible solid donut though Square becomes the surface of a donut.
The abstract gluing is to imagine what glued without distorting Cube. All of 8 vertices gather at a point where 8 corners fit each other perfectly without any gap or wrinkle as shown Fig. (8).
Both Cube and this abstract glued object are commonly called 3-torus.
The abstract glued object is three-dimensional but we can not draw it because of abstract. And it is nameless. If we were in the four-dimensional, we could see it. But it is impossible. 2-torus has its representation as a donut but 3-torus has none.
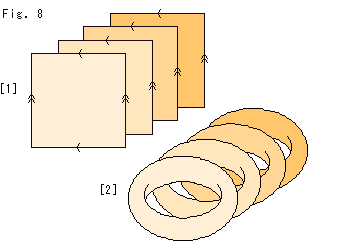
Nevertheless, let us try to visualize as much as possible. If we slice an object, we can get reduce dimensions. But we do not know how to slice the abstract glued object. So we slice Cube, and think of gluing sliced ones.
Fig. (9) shows infinite Square that are sliced sheets of Cube. They are cut in parallel with a face and have no thickness.
Fig. (10) shows donut surfaces made of Square. Now all we have to do is to pile them (surfaces) up. But it can not be done physically. Yet, isn't it easier for your imagination?
The abstract glued object is a strange solid with 1 vertex, 3 edges, 3 faces.
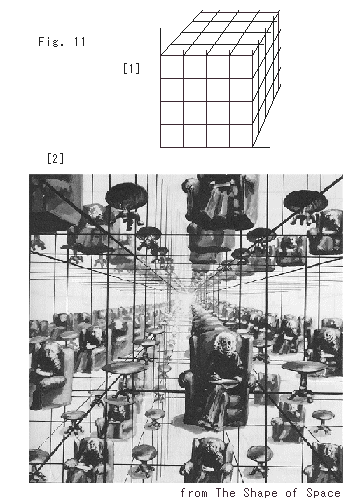
Fig. (11) shows it. It is drawn by force. Well, it is of no use whatever we compromise with it.
Euclidean geometry stands up in Cube. So we can say that
3-torus has Euclidean geometry.
It may better not to look at Fig. (11), which would confuse you.
There is no Euler number to see a topological character of three-dimensional object. (cf. "Euler number on 3-D" in next chapter)
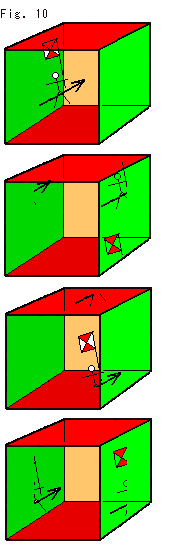
How does a moving object look like in Cube?
Fig. (12) is an imagined four-frame comic strip using Cube, which is semi-transparent. When a knight is touches the right wall, he reappears at the left wall. Look at his flag. When it touches the ceiling, it comes out from the floor.
Thus, though we are unable to see the outside of the abstract glued object, we can see its inside!
Fig. (13) below is 3-D tiles.
Fig. (14) shows Einstein sitting in the 3-D tiles. It looks as if there are infinite Einstein. But truly he is one.
The shape of universe might be 3-torus if the same matters or something are repeatedly observed like Fig. (14). Actually astronomers are trying to confirm it, and they say that some evidences have already been found.
* * * * * * * * * *
Now a regular octagon. hyperbolic geometry comes out.
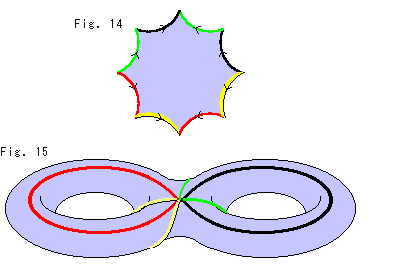
Get ready with a regular octagon that is marked as shown in Fig. (15). Suppose it is made of rubber as usual. We are going to glue edges and get a curved smooth surface. But we can not do it well. Because the sum of interior angles will be over 2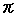 and they make wrinkles. We have to reduce every interior angle.
There is a smart procedure to do it. We embed the octagon in Poincare disk and adjust size as shown in Fig. (16). Then we get a suitable octagon that is a regular hyperbolic octagon colored in red. The sum of interior angles is now exactly 2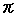. (Each interior angle is 45
.)
We call this regular hyperbolic octagon with interior angles of 45 and marks on edges for gluing Hyperbolic Octagon for short.
Using this Hyperbolic Octagon (Fig. (17)), we make a surface of double-float as shown Fig. (18).
You can creep on the double-float wherever you like without crossing any of red, green, black and yellow lines. It is natural because the double-float is made of Hyperbolic Octagon in Fig. (17).
By watching only Hyperbolic Octagon, it is not easy to foresee that Hyperbolic Octagon becomes a surface of double-float, isn't it?
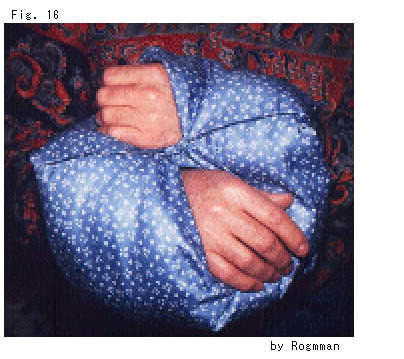
Fig. (20) shows that Sascha Rogmann passes his hands through holes of a double-float made of cloth. You may see How to make. It is fun.
Abstract gluing of Hyperbolic Octagon does not deform its shape. Naturally we can not see what glued. The double-float surface is a representation of it. The double-float has two holes. There are floats for three and more men in mathematics. Number of holes is called genus and denoted by g. Hyperbolic Octagon, the double-float surface and the abstract glued object are commonly called 2-torus of genus 2. Genus 1 is for one holed torus (donut surface, single-float surface).
Hyperbolic Octagon is not only edges but also inside is hyperbolic. That is, transformation from the regular octagon to Hyperbolic Octagon is not simple deformation. It is a qualitative change to hyperbolic. Since the regular octagon has not been defined as Euclidean or any geometric, it may be better to use word "given" instead of "change". Say, "Hyperbolic geometry is given." Anyhow, hyperbolic geometry stands in Hyperbolic Octagon. So it is said that
2-torus of genus 2 has hyperbolic geometry.
Also they often say that the double-float has hyperbolic geometry.
It does not matter if we use glasses frames instead of the double-float.
And it is called geometrization that the regular octagon is changed into Hyperbolic Octagon that has interior angles of 45. It is also said that hyperbolic structure is given.
Let us see Euler number. Since 2-torus of genus 2 has 1 vertex, 4 edges and 1 face,
= v - e + f
= 1 - 4 + 1 = -2 .
They say that it is hyperbolic if is negative.
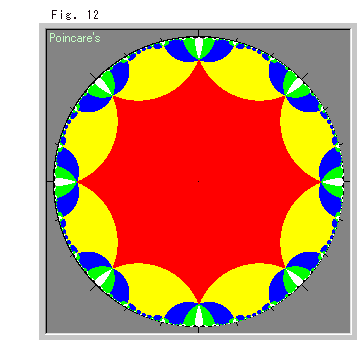
Fig. (21) shows tiling of colored Hyperbolic Octagon in Poincare disk. This time, we can spread tiles far to infinity. Every vertex is surrounded by eight of Hyperbolic Octagon. It is not similar case of a hyperbolic triangle.
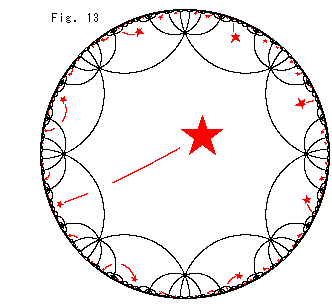
Fig. (22) shows moving in Hyperbolic Octagon. All of them move simultaneously.
The movement of a point in Fig. (17) is that if it is going out of one of red edges, it reappears another red edge (not opposite side). When it reaches at a vertex it appears at all of eight vertices.
(We have some more things to describe, but let us go ahead. A picture like Fig. (3') is one in mind though.)
* * * * * * * * * *
What will happen if genus g is more than 2?
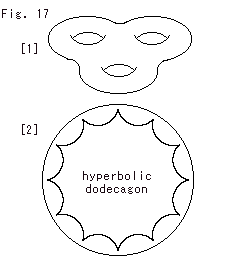
Fig. (23) is in case of genus 3. Euler number is easily counted by using genus g. That is,
= 2 - 2g
When g > 1, < 0.
Therefore, we can say that
2-torus (g > 1) has hyperbolic geometry.
* * * * * * * * * *
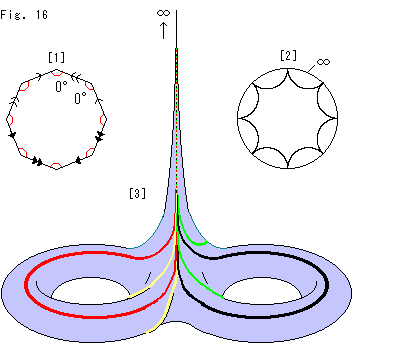
Fig. (24) shows a glued product of the largest regular hyperbolic octagon in Fig. (16). Every vertex of this hyperbolic octagon extends to infinity with zero interior angle. All vertices, we guess, gather at a point of infinity when glued.
Next: Ch.34 Conclusion
Prev: Ch.32 H(+) Space (Ideal Tetrahedron)
Table of Contents Index