True Character of Vertices
Poor knot K! It was transformed into vertex V, which was cut off. Let us fumble around the vertex V of that strange solid.
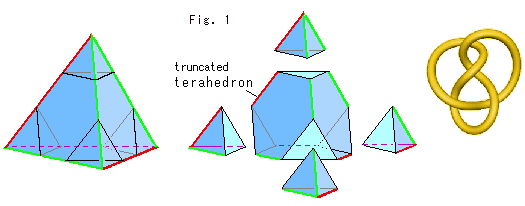
We take tetrahedron T with vertices, and cut around them as shown Fig. (1). It corresponds to a fat knot K like Fig. (1'). Do the same on terahedron T'. Then we get 8 small tetrahedra. Let us call them "mini-tetrahedra" for the time being. And let sections of mini-tetrahedra be bases. Denote vertices that are not on bases by a small letter v. Mini-tetrahedra have non-empty interior just as tetrahedra T. A tetrahedron of which corners are cut off is called a truncated tetrahedron.
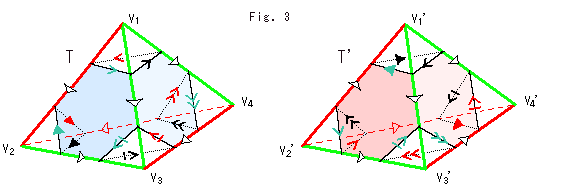
 Mark an arrow at every base edge of mini-triangle as shown Fig. (2). Any arrow is different from others. Fig. (2') shows arrows of tetrahedron T' following the gluing rule previously described.
Mark an arrow at every base edge of mini-triangle as shown Fig. (2). Any arrow is different from others. Fig. (2') shows arrows of tetrahedron T' following the gluing rule previously described.
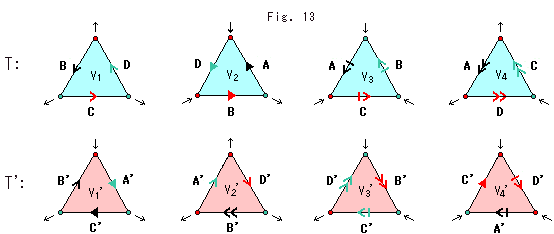
It is easy to confuse yourself if you try to make Fig. (2') at a stroke from Fig. (2), isn't it? Fig. (2') is constructed taking an arrow on every face of tetrahedron T. For example, arrows on face B and face B' are as shown in Fig. (3). See what relations of an arrow on face B with directions of red and green sides, and mark the same arrow where it has the same relations on face B'.
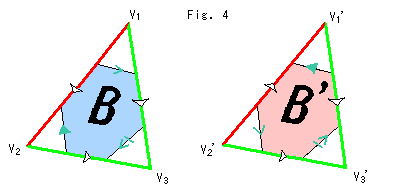
Fig. (4) below shows bases (triangles) of Mini-tetrahedra with these arrows. They are views from vertices of tetrahedra T and T'. Sky blue ones are of tetrahedron T and pink ones are of tetrahedron T'. Edges of tetrahedra T and T' are shown by small circles at vertices and black thin arrows around triangles. If a thin black arrow is directed inner, the edge directs to the vertex. And if the arrow is directed outer, the edge directs to the opposite.
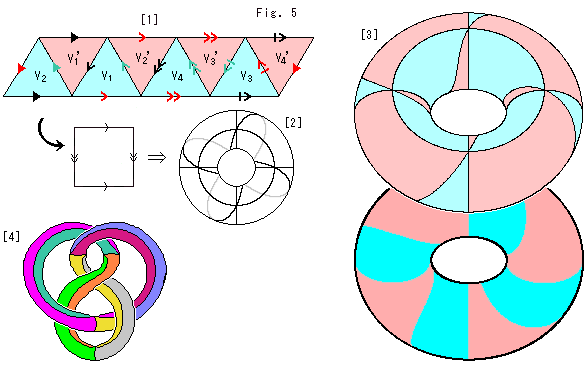 Chain these 8 bases of Mini-tetrahedra to meet their sides as the left picture of Fig. (5).
Chain these 8 bases of Mini-tetrahedra to meet their sides as the left picture of Fig. (5).
Now look around the chain. It forms that square with arrow marks (cf. Ch.33). It is a torus. This is the boundary surface between a fat knot K and the strange solid.
To get a torus in the shape of donut, you first make a cylinder by rolling up the square forward (reader's side) or backward (beyond the screen) (cf. Ch.33). If you consider that the front surface is different from the back, you must choose either forward rolling or backward. Suppose mini-tetrahedra in Fig. (5) are transparent except bases. Then vertices v (not on bases) are in reader's side. If you roll up the square forward, all mini-tetrahedra are packed inside of the donut gathering all vertices v at a point. The left picture in Fig. (5') shows this situation drawn by force. It looks 8 mini-tetrahedra are sitting
in a small area, but actually they occupy whole inside of the donut. You should imagine so.
To the contrary if you roll up the square backward, all mini-tetrahedra stand on outside of the donut gathering all vertices v at a point. The right picture in Fig. (5') shows this situation drawn by force. It looks 8 mini-tetrahedra are floating in midair, but actually they are sitting on entire surface of the donut. So imagine, please.
Actually both imagination are correct. Anyhow the boundary surface between the fat knot K and the strange solid is a torus. The left picture in Fig. (5'') shows 8 triangles in Fig. (5) tiled on the torus. These triangles are very deformed as if rubber films. They form triangulation (cf. Ch.29).
Also these triangles tile the fat knot K as the right picture in Fig. (5''). It is clarified that the torus and the fat knot K are homeomorphic.
In topology we have no interest in size. Therefore the torus and fat knot K do not change their appearance when we get smaller mini-tetrahedra. It can be interpreted that the torus is a transformed knot K. What we untwisted films F and F' was actually straightening out a tangled the knot K. This situation seems not to change even if the knot K has no thickness.
If we cut off real vertices (points) of tetrahedra T and T', suddenly we can not make triangles (bases) in Fig. (4).
 What will happen if we choose a point at infinity
What will happen if we choose a point at infinity  or
or  k?
k?
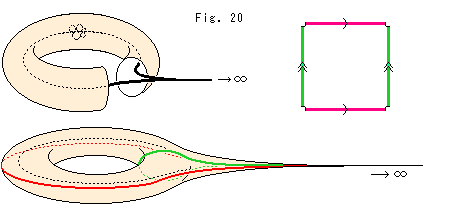
The donut surface of Fig. (5'') will have a cusp as shown Fig. (6). The cusp extends to infinity. Four corners of a square with arrows for the donut are lack because the cusp has an open end point.
Fig. (6') shows the fat knot K that passes through a point at infinity. In this case, bases of mini-tetrahedra has no vertices (Fig. (6'')).
If the point at infinity is  k rather than
k rather than  , we imagine that the original knot K is changed to have such shape.
, we imagine that the original knot K is changed to have such shape.
 Look at Fig. (7). We may guess that the cusp has an unlimitedly small hole at the tip. If we can get it push back to main body and enlarge the hole, we get a torus with a hole. Enlarge the hole more, then we get a picture at the right in Fig. (7).
Look at Fig. (7). We may guess that the cusp has an unlimitedly small hole at the tip. If we can get it push back to main body and enlarge the hole, we get a torus with a hole. Enlarge the hole more, then we get a picture at the right in Fig. (7).
However, it followed a condition that the cusp has an end point with a clear hole, that is, a boundary. You see, the cusp is forwarding to a point at infinity  and it is not closed. Therefore, Fig. (7) is nonsense. Though it is right, isn't it worth thinking, is it?
and it is not closed. Therefore, Fig. (7) is nonsense. Though it is right, isn't it worth thinking, is it?
Back



 Mark an arrow at every base edge of mini-triangle as shown Fig. (2). Any arrow is different from others. Fig. (2') shows arrows of tetrahedron T' following the gluing rule previously described.
Mark an arrow at every base edge of mini-triangle as shown Fig. (2). Any arrow is different from others. Fig. (2') shows arrows of tetrahedron T' following the gluing rule previously described.
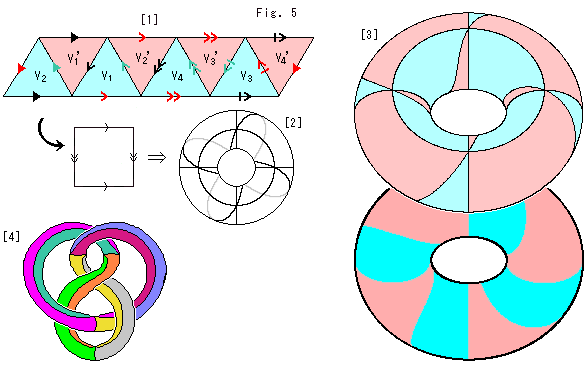 Chain these 8 bases of Mini-tetrahedra to meet their sides as the left picture of Fig. (5).
Chain these 8 bases of Mini-tetrahedra to meet their sides as the left picture of Fig. (5). What will happen if we choose a point at infinity
What will happen if we choose a point at infinity  Look at Fig. (7). We may guess that the cusp has an unlimitedly small hole at the tip. If we can get it push back to main body and enlarge the hole, we get a torus with a hole. Enlarge the hole more, then we get a picture at the right in Fig. (7).
Look at Fig. (7). We may guess that the cusp has an unlimitedly small hole at the tip. If we can get it push back to main body and enlarge the hole, we get a torus with a hole. Enlarge the hole more, then we get a picture at the right in Fig. (7).