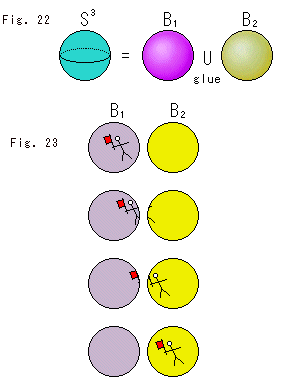[Back] [Next] [Contents]
Hyperbolic Non-Euclidean World
Ch. 49 Figure-8 Knot (1) 
There is a knot called the figure-8 knot. It is a knot shown at left top of Fig. 3 below. (You may glance the top of the next chapter Ch. 34, and back here.) We are going to enjoy the figure-8 knot. However, prior to it, we have to change our way of thinking. We need a quite new approach. Here we learn several items. As you guess, they are of topology.
Our key words here are homeomorphism, isotopy, identification, abstract gluing, a torus, embedding, geometrization, the hypersphere, and so on. Not only new words but also familiar words such as dimension, space and so on should be reconsidered. Let us see them.
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[Topology]
------Topology
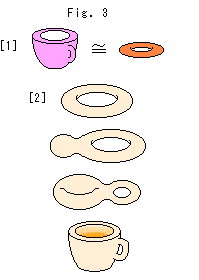 Topology is a way of thinking. It is difficult to define but easy to get familiar with. In topology we say that a coffee cup and a donut are topologically the same (homeomorphic) because both have a hole as shown Fig. 1. Symbol "
Topology is a way of thinking. It is difficult to define but easy to get familiar with. In topology we say that a coffee cup and a donut are topologically the same (homeomorphic) because both have a hole as shown Fig. 1. Symbol " " means homeomorphic to each other. We often use ordinary symbol "=" instead. Under a homeomorphism you may deform any object as long as you do not break, tear, or glue it. First of all, we do not care about definite shape or size or location. We regard an object as a set of points. Therefore, to keep homeomorphism you must not disconnect what was connected, nor connect what was not. It is just like a map drawn on a rubber sheet.
" means homeomorphic to each other. We often use ordinary symbol "=" instead. Under a homeomorphism you may deform any object as long as you do not break, tear, or glue it. First of all, we do not care about definite shape or size or location. We regard an object as a set of points. Therefore, to keep homeomorphism you must not disconnect what was connected, nor connect what was not. It is just like a map drawn on a rubber sheet.
Suppose the donut is made of clay. Then you can deform and change it to a coffee cup without tear or rejoin as shown in Fig. 2. Homeomorphism is kept all the way of deformation.
That is to say, in homeomorphism
"adjoining points are adjoining, and separate points are separating"
must be kept.
Let us call it the rule of homeomorphism.
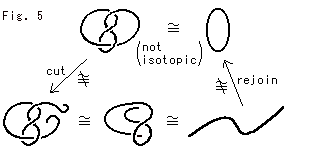 Look at Fig. 3. The loop and knot are homeomorphic but not isotopic. They can not be congruent however deformed unless we cut and rejoin either of them. But they are still homeomorphic. Whether homeomorphic or not depends on a period when we judge. It is not necessary for homeomorphism to be homeomorphic all the way or real-time. For example, you cut the string of an entangled knot, and then make it an ordinary loop by rejoining after disentanglement. Even if the knot has thickness, it is OK by fitting cut-outs as they were. In Fig. 2 the coffee cup and donut are homeomorphic even if we make the coffee cup by breaking the donut in pices and reassemble.
Look at Fig. 3. The loop and knot are homeomorphic but not isotopic. They can not be congruent however deformed unless we cut and rejoin either of them. But they are still homeomorphic. Whether homeomorphic or not depends on a period when we judge. It is not necessary for homeomorphism to be homeomorphic all the way or real-time. For example, you cut the string of an entangled knot, and then make it an ordinary loop by rejoining after disentanglement. Even if the knot has thickness, it is OK by fitting cut-outs as they were. In Fig. 2 the coffee cup and donut are homeomorphic even if we make the coffee cup by breaking the donut in pices and reassemble.
Isotopy is a concept for objects in a common space. In Fig. 3 the knot and loop are to be judged on condition that they are in the same space. Homeomorphism is a concept that does not require a common space. Homeomorphism can also be in abstract.
------Geometry
Geometry is an oppositional term to topology. It has two meanings. One is to measure an object and the other is to keep distances or metric. That is, it is a field where no distortion is allowed.
------Dimensions
In topology a curved line is 1-dimensional, a curved surface is 2-dimensional and a solid body is 3-dimensional. And however they are deformed their dimensions do not change. In other words, we pay attention to the object itself rather than a space where it is embedded. If an object has only a length, it is 1-dimensional. If an object has only an area, it is 2-dimensional. And if an object has only a volume (non-empty interior), it is 3-dimensional. Say a balloon in the sky is 2-dimensional because it is only a skin.
As to space, dimensions are given or we define.
------Space
Space is not necessary to be three or more dimensional. It does not always require expanse of length, breadth and height. A curved surface is 2-dimensional space. A line is 1-dimensional space. And we say that a point is zero-dimensional space. What is called manifold is a space. The hypersphere that we discuss later is also a space.
------Mapping
This reminds us  in the morning. There is the whole universe in our coffee cup now! We drink the universe every morning, don't we? We guess that points in coffee and points in the universe correspond to each other by one to one mapping. Because both have infinite number of points. And we can guess there is one to one mapping between them. To be homeomorphic, it is not enough. We do not know whether they are homeomorphic or not.
in the morning. There is the whole universe in our coffee cup now! We drink the universe every morning, don't we? We guess that points in coffee and points in the universe correspond to each other by one to one mapping. Because both have infinite number of points. And we can guess there is one to one mapping between them. To be homeomorphic, it is not enough. We do not know whether they are homeomorphic or not.
We do not need to think about the outside of coffee when we pay attention only to the inside coffee cup. You may regard coffee as the whole universe. But the outside of the coffee cup still exists.
------Identification
Look at Fig. 4.
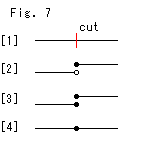 [a]: Suppose a line is cut.
[a]: Suppose a line is cut.
[b]: If one end is an open end point (black dot), the other end is a closed end point (white dot). It is usual, isn't it?
[c]: However, in topology we identify one end point with the other endpoint. As to open or closed, we think separately.
[d]: Now both ends are rejoined by identifing.
[e]: The identification is applied to faces of solids. The idea of identification can also be applied to any dimentional objects.
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[Torus]
------Donut
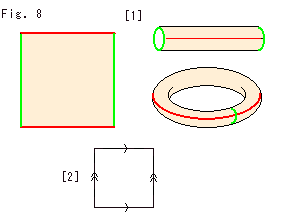
Here is a square. Suppose it is made of rubber. Make a cylinder and join the both ends without twisting as shown Fig. 5. Then we get a donut surface.
Four corners of the square gather at a point (intersection of Green and Red lines) on the donut. Sum of four interior angles is exactly 2 (45
(45 each) at a point without any gap or wrinkle.
each) at a point without any gap or wrinkle.
We mark arrows on edges of the square to indicate this gluing (identifying) method as shown Fig. 6. The donut surface and the sure with arrows are homeomorphic though they look different.
Hereafter we call this square with this gluing agreement the Square for short.
------Abstract gluing
We fictitiously imagine what abstractly glued without distorting the Square. It is absolutely abstract so that we can not make any image. But we can think of or feel the abstract object.
It can be said that the Square not only has the abstract gluing agreement but also represents the abstract object. The donut surface is what physically glued by force. That means the Square is distorted.
The abstract object is essence. It is not only invisible but also nameless.
Our abstract gluing never make deformation. In other words, if a shape is defined, we keep it.
We will apply this way of thinking to other objects, too.
By the way, have you ever seen Euclidean space from the outside? No. Who has? We have seen only the inside.
------Generic name
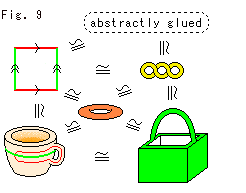 A generic name for the Square, the donut surface and the abstract glued object is torus, or 2-torus when we specify it two-dimensional.
A generic name for the Square, the donut surface and the abstract glued object is torus, or 2-torus when we specify it two-dimensional.
Topologists often use a common word without distinguishment. For example, Fig. 7 shows some different objects, coffee cup, a donut, the Square and so on. The red and gree curves on the coffee cup correspond to edges of the Square. Topologists call all of them in one word, torus. Because they are homeomorphic. But we are not used to such wording, so we should be careful.
The author sometimes feel that everything is a torus when a topologist talks. Of course, it is not true.
The abstract glued object is invisible but homeomorphic because it is not distorted at all.
------Euclidean geometry
We define that Euclidean geometry stands inside the Square. In other words, it is not self-evident that Euclidean geometry stands, and we set (embed) the Square in Euclidean world. Then we say that
2-torus has Euclidean geometry.
Though you might feel strange but we sometimes say that the donut surface has Euclidean geometry.
We can make it sure by using Euler number  (cf. Ch.29). Since the torus has 1 vertex, 2 edges, and 1 face,
(cf. Ch.29). Since the torus has 1 vertex, 2 edges, and 1 face,
 = v - e + f
= v - e + f
= 1 - 2 + 1 = 0 .
It is Euclidean for  is zero.
is zero.
------On 2-torus
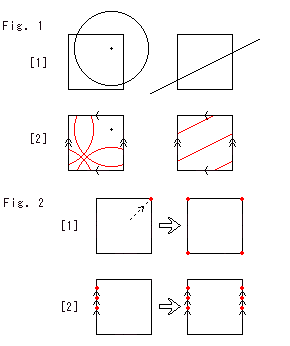
On the donut surface we can make a circuit tour through or around the hole and get back to the start area. In the Square, due to the identity of edges, you can never kick the right edge but your legs reappear from the left edge. When you hit a ball up, you can catch it at your feet. The square is finite domain without boundary.
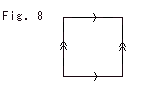
Fig. 8 shows a circle and a straight line on an ordinary square.
Fig. 8' shows the same movement as Fig. 7 but on the Square. Remember the Square is not deformed. It is not rubber.
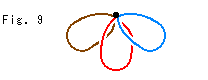
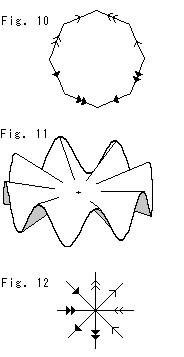
Fig. 9 is a special case.
[a]: Four points (actually one point) simultaneously appear at four corners when a point touches a corner.
[b]: When a point moves on an edge as an orbit, another point (actually the same point) moves on the opposite edge.
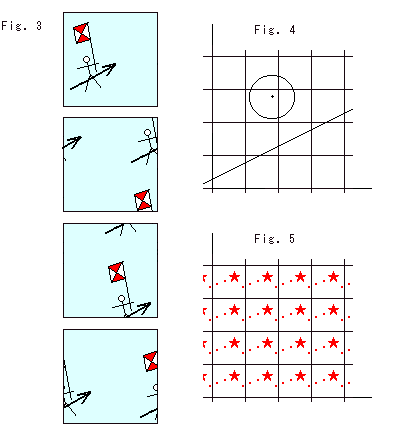
Fig. 10 is four-frame comic strip of a running knight on the Square. He never disappear though he looks as if cut into pieces. Wherever he runs, he stays in the Square.
Fig. 11 is a lattice with an agreement that any location is measured in each box. That is, infinite Squares are tiled. Then what we ordinarily draw a circle or a line expresses the same thing that we draw in the Square.
Fig. 12 is the same lattice as in Fig. 11 but based on different idea. A resident on the donut surface can not leave it because it is his whole world. In whichever direction he travels, he comes back where he left. That means, on the donut, he sees his own back. On the lattice identical men and matters are exist in every box. Fig. 12 shows what he observes in his world. Now all  moved simultaneously.
moved simultaneously.
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[3-Torus]
------Cube
This time we think of a cube. The cube is solid and three-dimensional.
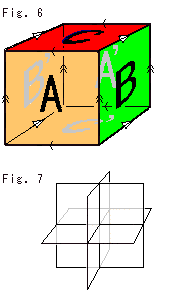 Look at Fig. 13. Direction of each face of this cube is indicated with arrows on edges. A face is identified with that of opposite side, and to be glued outside to outside. We call the cube with this gluing agreement the Cube for short.
Look at Fig. 13. Direction of each face of this cube is indicated with arrows on edges. A face is identified with that of opposite side, and to be glued outside to outside. We call the cube with this gluing agreement the Cube for short.
It is impossible to glue faces of the Cube physically with the gluing agreement. We have to do it abstractly. But do not guess it done in the four-dimensional world like SF novels. We must do it in three-dimensional space.
Do not guess that the Cube becomes a visible solid donut though the Square became the surface of a donut.
All of 8 vertices gather at a point by the abstract gluing. 8 corners perfectly fit each other without any gap or wrinkle as shown Fig. 14.
Both the Cube and this abstract glued object are commonly called 3-torus.
------Slicing
The abstract glued object is three-dimensional but we can not draw it because of abstract. And it is nameless. If we were in the four-dimensional world, we could see it. But it is impossible. 2-torus has its representation as a donut but 3-torus has none.
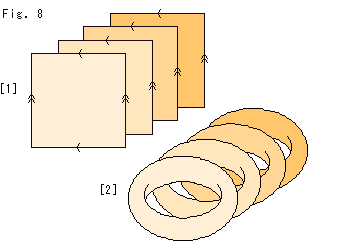 Nevertheless, let us try to visualize as much as possible. If we slice an object, we can get reduce dimensions. But we do not know how to slice the abstract glued object. So we slice the Cube, and think of gluing slices.
Nevertheless, let us try to visualize as much as possible. If we slice an object, we can get reduce dimensions. But we do not know how to slice the abstract glued object. So we slice the Cube, and think of gluing slices.
Fig. 15 shows infinite number of squares that are slices of the Cube. Each of them is the same as the Square described first. They are cut in parallel with a face and have no thickness.
Fig. 16 shows donut surfaces made of these squares. Now all we have to do is to pile them (surfaces) up. But it can not be done physically.
------Types of drawings
 The abstract glued object is a strange solid with 1 vertex, 3 edges, 3 faces.
The abstract glued object is a strange solid with 1 vertex, 3 edges, 3 faces.
There are several types of drawings besides ordinary drawings. For instance, a forced drawing, a symbolic diagram, a slice drwing, and a comical drawing. We, of course, have no abstract drawing. We are not abstract painters.
Fig. 17 shows a forced drawing of the strange solid. A slice drawing is like Fig. 16. A symbolic drawing is, for example, Fig. 5 or 6 for the Cube. In this case the imension of Cube is reduced by 1. A symbolic drawing is also called a schematic diagram.
------Euclidean geometry
We embed the Cube in Euclidean space similarly to the Square. So we say that
3-torus has Euclidean geometry.
Fig. 17 may confuse us. We had better to see the Qube with imagination.
There is no Euler number to see a topological character of three-dimensional object. (cf. "Euler number on 3-D" in the next chapter)
------In 3-torus
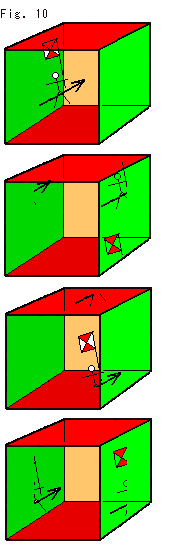
 How does a moving object look like in the Cube?
How does a moving object look like in the Cube?
Fig. 18 is an imagined four-frame comic strip using the Cube, which is semi-transparent. When a knight is touches the right wall, he reappears at the left wall. Look at his flag. When it touches the ceiling, it comes out from the floor.
Thus, though we are unable to see the outside of the abstract glued object, we can see its the inside!
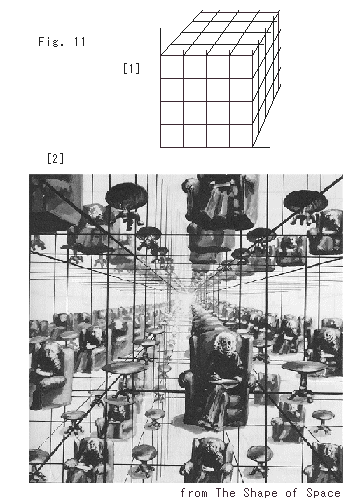
Fig. 19 is 3-D tiles of the Cube.
Fig. 20 shows Einstein sitting in the 3-D tiles. It looks as if there are infinite Einstein. But truly he is one. He is seeing his own back.
The shape of universe might be 3-torus if the same matter or something is repeatedly observed like Fig. 20. Actually astronomers are trying to confirm it, and they say that some evidences have already been found.
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[2-holed Torus]
------Regular Octagon
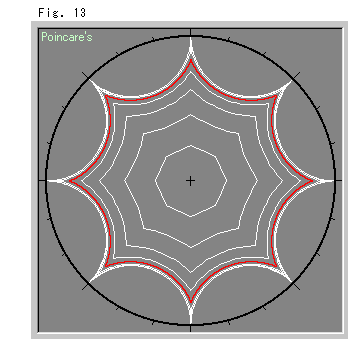
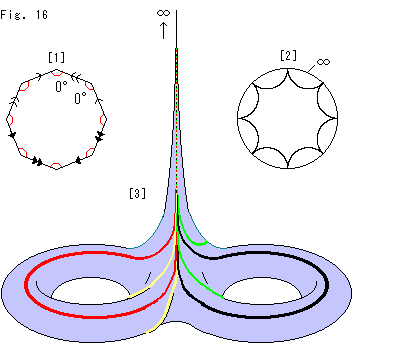
Now a regular octagon. The hyperbolic geometry comes out!
Get ready with a regular octagon that is marked as shown in Fig. 21. Suppose it is made of rubber as usual. We are going to glue edges and get a curved smooth surface. But we can not do it well. Because when 8 vertices gather at a point, the sum of interior angles will be over 2 and they make wrinkles as shown Fig. 22. 8 corners must be gathered as shown Fig. 23. We have to reduce every interior angle.
and they make wrinkles as shown Fig. 22. 8 corners must be gathered as shown Fig. 23. We have to reduce every interior angle.
There is a smart procedure to do it. We embed the octagon in Poincare disk and adjust size as shown in Fig. 24. Then we get a suitable octagon that is a regular hyperbolic octagon colored in red. The sum of interior angles is now exactly 2 . (The hyperbolic radius of the circumcircle is approximately 2.45, which is 0.841 in the model (unit disk).)
. (The hyperbolic radius of the circumcircle is approximately 2.45, which is 0.841 in the model (unit disk).)
This regular hyperbolic octagon has interior angles of 45 and marks on edges for the gluing. We call it Hyperbolic Octagon for short.
and marks on edges for the gluing. We call it Hyperbolic Octagon for short.
------Double-float
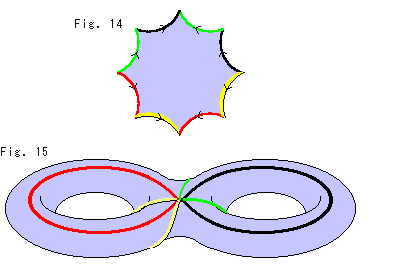
Fig. 25 is the Hyperbolic Octagon with colored edges.
Fig. 26 shows a surface of double-float made of the Hyperbolic Octagon in Fig. 25.
You can creep on the double-float wherever you like without crossing any of red, green, black or yellow lines. It is natural because the double-float is made of Hyperbolic Octagon in Fig. 25.
By watching only the Hyperbolic Octagon, it is not easy to foresee that Hyperbolic Octagon becomes a surface of double-float, isn't it?
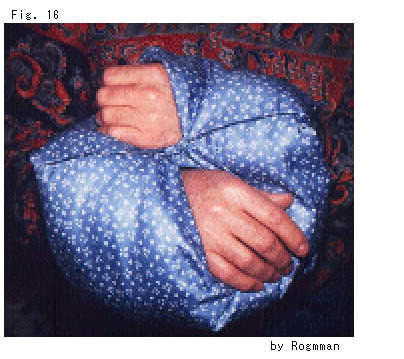
Fig. 27 shows that Sascha Rogmann passes his hands through holes of a double-float made of cloth. You may see How to make. Have fun.
Abstract gluing of the Hyperbolic Octagon does not deform its shape as usual. Naturally we can not see what abstractly glued. The double-float surface is a representation of it.
The double-float has two holes. Therefore, the Hyperbolic Octagon, the double-float surface and the abstract glued object are commonly called 2-holed torus.
------Hyperbolic geometry
The Hyperbolic Octagon is hyperbolic not only on edges but also the inside. That is, transformation from the regular octagon to the Hyperbolic Octagon is not simple deformation. It is a qualitative change to hyperbolic. Since the regular octagon has not been defined as Euclidean or any geometric, it may be better to use a word "given" instead of "change". Say, "Hyperbolic geometry is given."
Anyhow, hyperbolic geometry stands in Hyperbolic Octagon. So it is said that
2-holed torus has hyperbolic geometry.
Or,
2-holed torus has hyperbolic geometry.
Also they often say that the double-float has hyperbolic geometry.
It does not matter if we use glasses frames instead of the double-float because they are homeomorphic.
And it is called geometrization that the regular octagon is changed into the Hyperbolic Octagon that has interior angles of 45 . It is also said that hyperbolic structure is given.
. It is also said that hyperbolic structure is given.
Let us see Euler number. Since 2-holed torus has 1 vertex, 4 edges and 1 face,
 = v - e + f
= v - e + f
= 1 - 4 + 1 = -2 .
We say that it is hyperbolic because  is negative.
is negative.
------Tiling
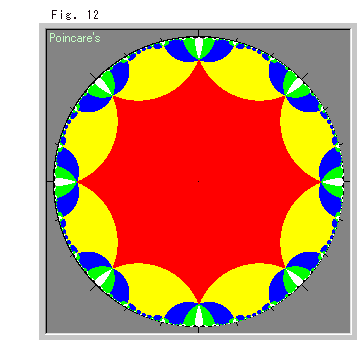 Fig. 28 shows the tiling of colored Hyperbolic Octagon in Poincare disk. This time, we can spread tiles far to infinity. Every vertex is surrounded by eight of the Hyperbolic Octagon. It is not similar case of a hyperbolic triangle.
Fig. 28 shows the tiling of colored Hyperbolic Octagon in Poincare disk. This time, we can spread tiles far to infinity. Every vertex is surrounded by eight of the Hyperbolic Octagon. It is not similar case of a hyperbolic triangle.
------On the Hyperbolic Octagon
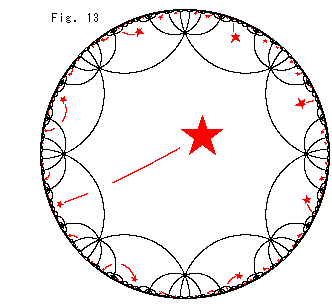 Fig. 29 shows infinite number of moving
Fig. 29 shows infinite number of moving  in the Hyperbolic Octagon. All of them move simultaneously.
in the Hyperbolic Octagon. All of them move simultaneously.
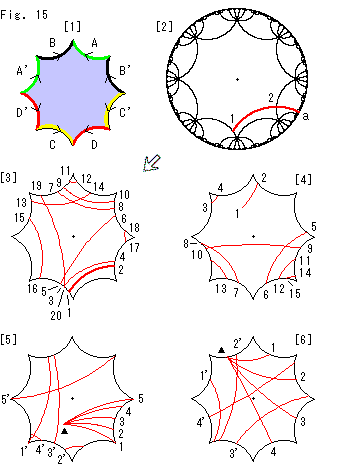
Fig. 30 is (hyperbolic) straight line on the Hyperbolic Octagon. A similar picture of Fig. 25 is put in the center left for easy observation. Vertically opposite angles at the intersection of an edge and the line is kept on the identified edges.
[a]: A half-line that is the red part of straight line in the Poincare disk (left top) is drawn in the Hyperbolic Octagon. The line starts at 1 on edge C and goes to 2 on edge C', and reappears at 3 on the identified edge C and goes to 4 on edge C'. Then it reappears at 5 on edge C. There the line goes right-up-ward to 6 on edge B' due to keeping vertically opposite angles. Now it reapper at 7 on edge B that is identified with edge B'. And so on.BR>
[b]: A start point and the slope of straight line is changed from [a]
[c]: Linens with various slopes at a fixed start point  . Line step such that 1 to 1', 2 to 2', 3 to 3'. The point 1 is on edge C' but not at vertex. The point 5 is exactly at the vertex between edges B' and C'.
. Line step such that 1 to 1', 2 to 2', 3 to 3'. The point 1 is on edge C' but not at vertex. The point 5 is exactly at the vertex between edges B' and C'.
The area around the point where 8 edges gather by gluing is shown in Fig. 30'. When a line reaches at a vertex, it will reappear at the opposite vertex. If the line makes its way exactly in middle of agacent edges (22.5 each), it will goes from the opposite vertex to the vertex where the line previously disappeared. And it will continuously repeat the samething. In this case the line goes through the origin and looks an ordinary straight line.
each), it will goes from the opposite vertex to the vertex where the line previously disappeared. And it will continuously repeat the samething. In this case the line goes through the origin and looks an ordinary straight line.
[d]: A start point  and the slope of straight line is changed from [c]
and the slope of straight line is changed from [c]
These pictures are quite different from Fig. 8'.
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[Genus]
There are floats for three and more men in mathematics. Number of holes is called genus and denoted by g. The 2-holed torus is also called 2-torus of genus 2. Genus 1 is for one holed torus (donut surface, single-float surface), and genus 0 is for a spherical surface.
What will happen if genus g is more than 2?
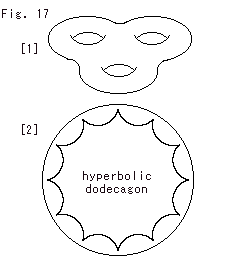
Fig. 31 is in case of genus 3. A hyperbolic dodecagon is obtained. Euler number  is easily counted by using genus g. That is,
is easily counted by using genus g. That is,
 = 2 - 2g
= 2 - 2g
When g > 1,  < 0.
< 0.
Therefore, we can say that
All of 2-tori which genus g is greater than 1 has hyperbolic geometry.
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[Ideal Octagon]
 The largest regular hyperbolic octagon in Fig. 24 is called an ideal octagon.
The largest regular hyperbolic octagon in Fig. 24 is called an ideal octagon.
Fig. 32 shows a glued product of it. Every vertex of the ideal octagon extends to infinity with zero interior angle. All vertices, we guess, gather at a point at infinity when glued.
Here we no more go into this subject.
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[Hypersphere]
What is the hypersphere  ? It is also called the three-sphere.
? It is also called the three-sphere.
We are usually not so conscious of space where we put a thing. There must be space when an object exists. However, in topology we do not define space in a case. We have known Euclidean space 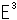 and the hyperbolic space
and the hyperbolic space 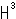 . The hypersphere
. The hypersphere  is a modified Euclidean space.
is a modified Euclidean space.
First, does 3-dimensional Euclidean space 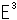 include a point at infinity
include a point at infinity  ? We are not sure. So we use so-called
? We are not sure. So we use so-called  and one of points at infinity
and one of points at infinity  .
.
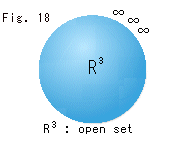 Look at Fig. 33.
Look at Fig. 33.  is in the 3-dimansional Euclidean space
is in the 3-dimansional Euclidean space 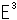 . We can set a point in
. We can set a point in  far from the origin as much as we want except the point at infinity
far from the origin as much as we want except the point at infinity  . We usually regard it as a sphere without boundary. It is just like a peeled apple and what is called an open set.
. We usually regard it as a sphere without boundary. It is just like a peeled apple and what is called an open set.
In the outside of  there are countless points at infinity
there are countless points at infinity  . But, in a case, we regard them as a single point. (cf. Ch. 23)
. But, in a case, we regard them as a single point. (cf. Ch. 23)
Of course, we can see its inside. But we can not observe  itself from the outside unless we stay in infinity
itself from the outside unless we stay in infinity  .
.
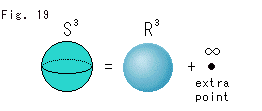 Fig. 34 shows how the hypersphere
Fig. 34 shows how the hypersphere  is made. It consists of
is made. It consists of  and an extra point that is not in
and an extra point that is not in  . We usually denote the extra point by
. We usually denote the extra point by  because it lives outside of
because it lives outside of  . The extra point can be any point as long as it is not included in
. The extra point can be any point as long as it is not included in  . But we usually denote it by
. But we usually denote it by  . And we take it as one of points at infinity for easiness.
. And we take it as one of points at infinity for easiness.
We can not see the hypersphere  because of abstract object though it is 3-dimensional. If we were in the four dimensional world, we could see the hypersphere
because of abstract object though it is 3-dimensional. If we were in the four dimensional world, we could see the hypersphere  .
.
------Another idea.
This time, we use two solid balls 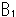 and
and 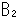 . It is okay to get the hypersphere
. It is okay to get the hypersphere  by the above procedure. But the following idea is usefull in general.
by the above procedure. But the following idea is usefull in general.
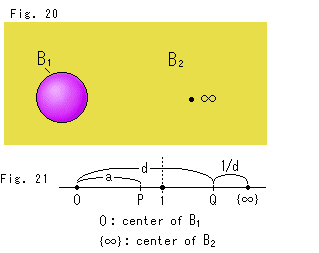 Look at Fig. 35. We divide
Look at Fig. 35. We divide  in two.
in two.
The ball  is the inside sphere with radius 1.
is the inside sphere with radius 1.
Another ball  contains all other points in
contains all other points in  together with the extra point
together with the extra point  .
.
The center of the ball  is the extra point
is the extra point  . That means two balls
. That means two balls 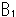 and
and 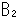 are image by inversion of each other.
are image by inversion of each other.
Now we glue the two balls 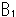 and
and 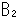 by face to face as shown in Fig. 35'. Then we get the hypersphere
by face to face as shown in Fig. 35'. Then we get the hypersphere  . Naturally the gluing can not be done physically but abstractly. Symbol U for gluing is the same as sum of sets because we consider the Balls as sets.
. Naturally the gluing can not be done physically but abstractly. Symbol U for gluing is the same as sum of sets because we consider the Balls as sets.
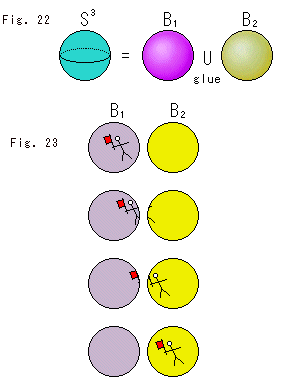
Fig. 36 shows a movement inside the hypersphere  . We regard the two solid balls
. We regard the two solid balls  and
and  as glued ones. When a man with a flag reaches at the surface of
as glued ones. When a man with a flag reaches at the surface of 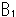 , he reappears at the surface of
, he reappears at the surface of 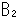 . And he freely walks in both Balls that is the hypersphere
. And he freely walks in both Balls that is the hypersphere  . He can also touch the extra point.
. He can also touch the extra point.
We guess that the hypersphere  would be visible if we were in the four dimensional world. In the web there are
would be visible if we were in the four dimensional world. In the web there are
Web1,
Web2,
Web3,
Web4,
Optiverse,
Outside In (Click "MPEG movie of everting sphere". It is a video.)
[Back] [Next] [Contents]
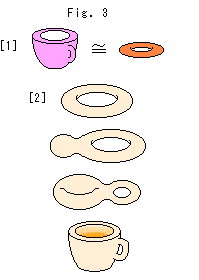 Topology is a way of thinking. It is difficult to define but easy to get familiar with. In topology we say that a coffee cup and a donut are topologically the same (homeomorphic) because both have a hole as shown Fig. 1. Symbol "
Topology is a way of thinking. It is difficult to define but easy to get familiar with. In topology we say that a coffee cup and a donut are topologically the same (homeomorphic) because both have a hole as shown Fig. 1. Symbol "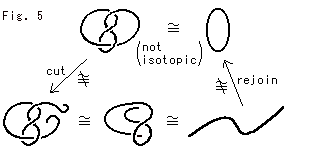 Look at Fig. 3. The loop and knot are homeomorphic but not isotopic. They can not be congruent however deformed unless we cut and rejoin either of them. But they are still homeomorphic. Whether homeomorphic or not depends on a period when we judge. It is not necessary for homeomorphism to be homeomorphic all the way or real-time. For example, you cut the string of an entangled knot, and then make it an ordinary loop by rejoining after disentanglement. Even if the knot has thickness, it is OK by fitting cut-outs as they were. In Fig. 2 the coffee cup and donut are homeomorphic even if we make the coffee cup by breaking the donut in pices and reassemble.
Look at Fig. 3. The loop and knot are homeomorphic but not isotopic. They can not be congruent however deformed unless we cut and rejoin either of them. But they are still homeomorphic. Whether homeomorphic or not depends on a period when we judge. It is not necessary for homeomorphism to be homeomorphic all the way or real-time. For example, you cut the string of an entangled knot, and then make it an ordinary loop by rejoining after disentanglement. Even if the knot has thickness, it is OK by fitting cut-outs as they were. In Fig. 2 the coffee cup and donut are homeomorphic even if we make the coffee cup by breaking the donut in pices and reassemble. [a]: Suppose a line is cut.
[a]: Suppose a line is cut.

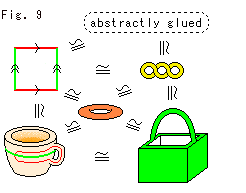 A generic name for the Square, the donut surface and the abstract glued object is torus, or 2-torus when we specify it two-dimensional.
A generic name for the Square, the donut surface and the abstract glued object is torus, or 2-torus when we specify it two-dimensional.

 Look at Fig. 13. Direction of each face of this cube is indicated with arrows on edges. A face is identified with that of opposite side, and to be glued outside to outside. We call the cube with this gluing agreement the Cube for short.
Look at Fig. 13. Direction of each face of this cube is indicated with arrows on edges. A face is identified with that of opposite side, and to be glued outside to outside. We call the cube with this gluing agreement the Cube for short. Nevertheless, let us try to visualize as much as possible. If we slice an object, we can get reduce dimensions. But we do not know how to slice the abstract glued object. So we slice the Cube, and think of gluing slices.
Nevertheless, let us try to visualize as much as possible. If we slice an object, we can get reduce dimensions. But we do not know how to slice the abstract glued object. So we slice the Cube, and think of gluing slices. The abstract glued object is a strange solid with 1 vertex, 3 edges, 3 faces.
The abstract glued object is a strange solid with 1 vertex, 3 edges, 3 faces.
 How does a moving object look like in the Cube?
How does a moving object look like in the Cube?



 Fig. 28 shows the tiling of colored Hyperbolic Octagon in Poincare disk. This time, we can spread tiles far to infinity. Every vertex is surrounded by eight of the Hyperbolic Octagon. It is not similar case of a hyperbolic triangle.
Fig. 28 shows the tiling of colored Hyperbolic Octagon in Poincare disk. This time, we can spread tiles far to infinity. Every vertex is surrounded by eight of the Hyperbolic Octagon. It is not similar case of a hyperbolic triangle. Fig. 29 shows infinite number of moving
Fig. 29 shows infinite number of moving 

 The largest regular hyperbolic octagon in Fig. 24 is called an ideal octagon.
The largest regular hyperbolic octagon in Fig. 24 is called an ideal octagon. Look at Fig. 33.
Look at Fig. 33. 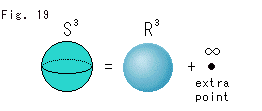 Fig. 34 shows how the hypersphere
Fig. 34 shows how the hypersphere  Look at Fig. 35. We divide
Look at Fig. 35. We divide