Hyperbolic Non-Euclidean World
Ch. 50 Figure-8 Knot (2) 
This chater is so large that you can jump to:
[Step1] [Step2] [Step3] [Addenda]
(Better to read the previous chapter Ch.33 if you haven't.)
They say that hyperbolic space comes out of what is called figure-8 knot.
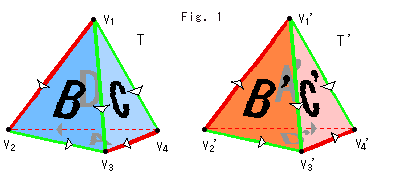
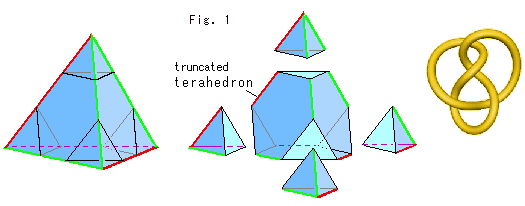
The figure-8 knot is a knot of string tied like Fig. 1 and jointed both ends shown in Fig. 1'. The string is a curved mathematical line, and never touches to itself though it goes over or under itself. That is, the figure-8 knot is a 3-D two-level self-crossing loop. We do not ask the size or shape of it. The diameter of the string is that of a point because a curved line consists of chained points. You may stretch both ends of the string in Fig. 1 up to infinity. It is still called figure-8 knot because the string makes a loop when attaching the point at infinity.
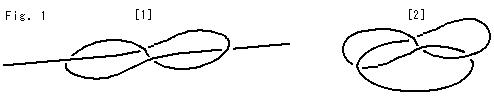

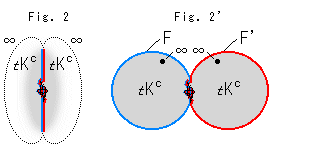
The figure-8 knot is often drawn as shown Fig. 2. Fig. 2' is an arranged copy from The KnotPlot Site. The side and back views of the figure-8 knot are the same as you see it now. Viewed from above is central symmetry. There are movable pictures on the Web, Elementary Topology. Fig. 2'' is a curtained picture of figure-8 knot to see which part is forward or backward. (Other drawings of the figure-8 knot are shown in Fig. 7 and Other pictures of figure-8 knot in [Addenda].)
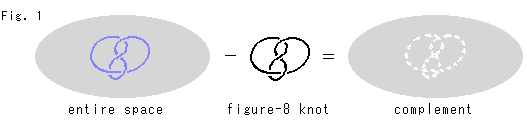
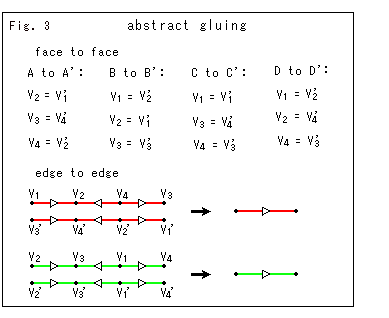
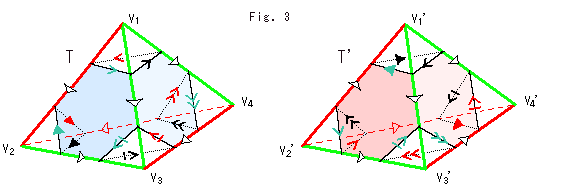
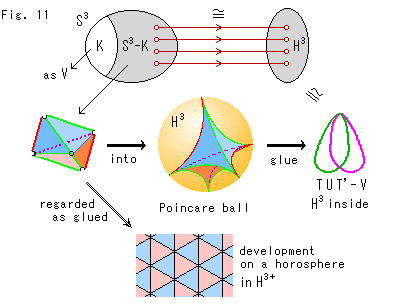
The complementary space of figure-8 knot is our subject. We say that the figure-8 knot has the simplest complement to treat. Complement is a space excluding the figure-8 knot that has lived in the space, namely all of space minus figure-8 knot. Mathematically, it is expressed that whole set (space) minus subset (figure-8 knot) equals to complementary set (complement. Fig. 3 shows this situation. And we say, "Complement is a hyperbolic space." Is that true?
In 1978 William P. Thurston discovered that the majority of knot complements are hyperbolic. (The only knots that are not hyperbolic are so-called torus knots and satellite knots.) And he received the Fields medal (the mathematics version of a Nobel prize) in 1982. In the reason for the prize, it is said that he did revolutionary work! (Before 1974, Robert Riley first discovered that the figure-8 is hyperbolic.)
What is it? Let us take the figure-8 knot and see Thurston's geometrization. Most of mathematicians I met said, "The figure-8 knot is hard to understand." But I begin to write about it without hesitation. You know, I am Don Quixote. (The world first popular book on the figure-8 knot!)
Thurston says that
the complement of the figure-8 knot can also be expressed
as the union of two tetrahedra in a particular way.
Mathematical expression of what he says is
| (1) |  - K = T U T' - V - K = T U T' - V |
| where | |
|
|  = the hypersphere = the hypersphere |
| | K = the figure-8 knot |
| | T, T' = tetrahedra |
| | U = glue (particular union) |
| | V = vertices of T U T'. |
* * * * * * *
First let us define our terms and symbols.
Original Comp  |
--- the complement expressed in the left side, |
|
 - K . - K . |
Topological Comp  |
--- the complement expressed in the right side, |
|
T U T' - V . |
Geometric Comp  |
--- the geometrilized complement (final object). |
All of these complements are homeomorphic,  =
=  =
=  .
.
Other symbols in our story will be defined when we use them.
Topological Comp  is a complement prior to the geometrization. It is what we are going to get first.
is a complement prior to the geometrization. It is what we are going to get first.
We often call the complement of the figure-8 knot "Complement" for short.
Also we often write "the knot K" instead of writing the figure-8 knot.
As to terms not explained in this chapter, see the previous chapter Ch.33.
You might think that we should have a loop instead of figure-8 knot from the beginning so that our story would be much easier. But it is no good because we have to get Topological Comp  of the knot K as a knot. The loop and knot K are homeomorphic but not isotopic. As to the knot K itself, we will not worry about keeping homeomorphism after we get its information (a shrink-wrapping or like of the knot K in our story) for Topological Comp
of the knot K as a knot. The loop and knot K are homeomorphic but not isotopic. As to the knot K itself, we will not worry about keeping homeomorphism after we get its information (a shrink-wrapping or like of the knot K in our story) for Topological Comp  . We must keep homeomorphism of the complement as a result.
. We must keep homeomorphism of the complement as a result.
* * * * * * *
Now, we interpret what Thurston says.
"the union ... in a particular way" means gluing with high technique and full imagination in our story. I would say, " It is a trick!" The gluing will be the key point.
"the complement ... be expressed ..." means that it is possible to change Original Comp  for Topological Comp
for Topological Comp  that is different from but homeomorphic to Original Comp
that is different from but homeomorphic to Original Comp  . What expressed is not Original Comp
. What expressed is not Original Comp  but Topological Comp
but Topological Comp  . They sometimes say, "A complement is taken apart in two tetrahedra." It has the same meaning.
. They sometimes say, "A complement is taken apart in two tetrahedra." It has the same meaning.
* * * * * * *
Let us go back to Formula (1).
The equal sign indicates that the left side and the right side are homeomorphic. We should use "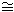 " but often use ordinary "=" instead.
" but often use ordinary "=" instead.
Formula (1), as well as oral expressions, does not mention what kind of space Topological Comp  is. It is our aim to see that Topological Comp
is. It is our aim to see that Topological Comp  is geometrilized and changed into Geometric Comp
is geometrilized and changed into Geometric Comp  that is hyperbolic.
that is hyperbolic.
About the left side of Formula (1).
The left side is the definition of Original Comp  . It is not numerical. We can not make the subtraction concretely.
. It is not numerical. We can not make the subtraction concretely.
The hypersphere  is a whole space in mind at the left side. And in the right side, T U T' is one to one mapping space to
is a whole space in mind at the left side. And in the right side, T U T' is one to one mapping space to  . Do not mistake mapping physical motion.
. Do not mistake mapping physical motion.
About the right side of Formula (1).
The right side of Formula (1) can not be gotten by calculating the left side or changing the right side itself. That is to say, the right side is to meet the left side only by telling a story. How fun it is!
We can not understand what tetrahedra T and T' only by observing Formula (1). We do not care about the size or distortion of tetrahedra. But they have non-empty interior. "non-empty interior" is a region where you can put or set up something. But do not think that some physical matters are packed.
Vertex V is a point that is an incarnation of the figure-8 knot.
* * * * * * *
Now, how do they get complement  out of the entire space
out of the entire space  ? How do they judge it hyperbolic?
? How do they judge it hyperbolic?
It is interesting that some mathematicians say this way for a subject and others say that way for the same subject. Anyway, let me begin the story.
S〜 say one thing and others another.
To begin with, we define symbols for tetrahedra T and T'. We will divide Original Comp  in two parts by films. Each part ia a complement that consists of a half of Original Comp
in two parts by films. Each part ia a complement that consists of a half of Original Comp  . Tetrahedra T and T' each will contain the complement.
. Tetrahedra T and T' each will contain the complement.
Half Comp  |
--- the complement in the tetrahedron T. |
Half Comp 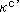 |
--- the complement in the tetrahedron T'. |
Films F and F' are to get Half Comp 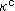 and
and 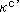 respectively.
respectively.
Our story takes three steps.
1. Assembling tetrahedra T and T', we get Half Comp 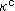 and
and 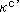 .
.
2. Gluing tetrahedra T and T' with vertex V deleted, we get Topological
Comp  .
.
3. Geometrization by replacing tetrahedra T and T' with regular ideal
tetrahedra. And Geometric Comp  that is hyperbolic space
that is hyperbolic space 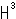 .
.
Needless to say, we should think all in topology until geometrization.
A space called hypersphere  is written in the left side of formula (1). But in the right side, a space to be pasted on films is not specified. Because it is not necessary to set a definite space for topological treatment.
is written in the left side of formula (1). But in the right side, a space to be pasted on films is not specified. Because it is not necessary to set a definite space for topological treatment.
We may cut off vertices of tetrahedra at any stage. But the Formula (1) looks to do it after gluing tetrahedra. So we do here.
Back to Top
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[Step 1]
Let the figure-8 knot be finite unless specified. Put it in  (
(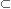
 ), and here we get tetrahedra T and T' with Half Comp
), and here we get tetrahedra T and T' with Half Comp 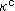 and
and  each.
each.
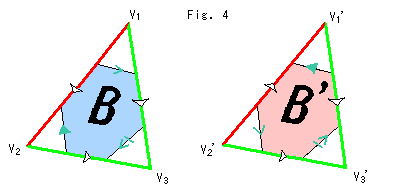
Look at Fig. 4. We use two films F (sky blue) and F' (pink). They are imaginary and unsubstantial. Sandwich the knot K between films F and F', and make it just like a shrink-wrapping. Films F and F' together divide Original Comp  in two parts that are Half Comp
in two parts that are Half Comp 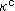 and
and  . Imagine that films F and F' are adhesive tapes, and paste Half Comp
. Imagine that films F and F' are adhesive tapes, and paste Half Comp 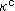 and
and 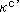 on them.
on them.
The picture at right bottom in Fig. 4 shows a cross section of the string of knot K with films F and F'. The picture at left bottom shows an image that Original Comp  is divided in two.
is divided in two.
 We consider films F and F' as spheres because they expand to infinity
We consider films F and F' as spheres because they expand to infinity  and get back to finite as shown in Fig. 5. Fig. 5' is an imaginary picture of their cross sections. But remember films F and F' are fully stuck (not at a point but covered the whole) each other though they are drawn separately in right and left. We can not say which side has a point of infinity but they actually have it commonly.
and get back to finite as shown in Fig. 5. Fig. 5' is an imaginary picture of their cross sections. But remember films F and F' are fully stuck (not at a point but covered the whole) each other though they are drawn separately in right and left. We can not say which side has a point of infinity but they actually have it commonly.
 Fig. 6 is a photo of the knot K with a film. It is made of a metal wire dipped in shampoo. Well, it is hard to see, isn't it? We are able to see a certain part of the film but not the whole. It is such that the wire with the film goes through another part of the film (the wire crosses in two-level and the film intersects itself). The film is transparent but it is not easy to see a construction beyond the film surface.
Fig. 6 is a photo of the knot K with a film. It is made of a metal wire dipped in shampoo. Well, it is hard to see, isn't it? We are able to see a certain part of the film but not the whole. It is such that the wire with the film goes through another part of the film (the wire crosses in two-level and the film intersects itself). The film is transparent but it is not easy to see a construction beyond the film surface.
You might think that the shape of the shampoo film is something like Moebius strip that has only one surface. But do not worry about it.
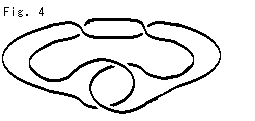 Fig. 7 shows another view of the knot K. It may melt your doubt. A film crosses itself and twists, but it has the front and back. It is also obvious if you recall that the knot K is a 3-D loop.
Fig. 7 shows another view of the knot K. It may melt your doubt. A film crosses itself and twists, but it has the front and back. It is also obvious if you recall that the knot K is a 3-D loop.
Therefore, it is no problem to divide Original Comp  in two.
in two.
However, there is no way to see the whole shape of the film on the knot K in the shape of Fig. 2 or like. So we try to cut the film in some pieces along intersection lines of the film. But, seeing Fig. 2'', there are so many color change points where the film intersects itself. We can not find proper cut-lines. So we refer to A Topological Picturebook by George K. Francis.
We will get the whole shape seeing Fig. 8 to 10 below.
See Shape of Film. Also you may visit Knot Spanning Surfaces in Web.
* * * * * * *
Let the film F make the tetrahedron T.
Fig. 8 shows its process. One side of the knot K is colored dark brown for easy to see. Gray area is the backside. The knot K is on the film F (sky blue) with Half Comp  .
.
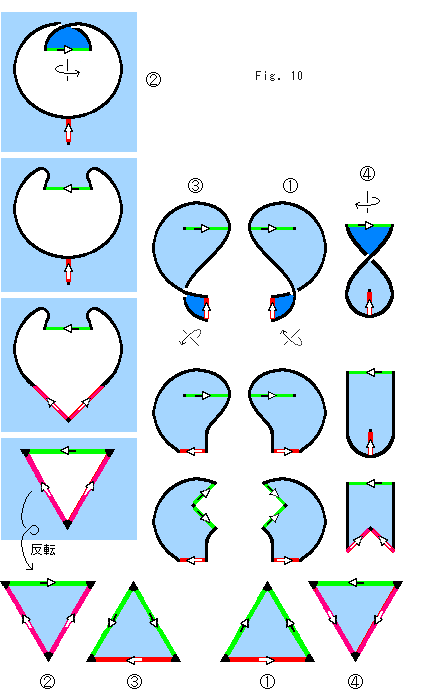 Figure (*) upper right shows the entire kno K with red and green partitions that will divide the film F together with the knot K in four. Small white delta on each partition indicates its direction.
Figure (*) upper right shows the entire kno K with red and green partitions that will divide the film F together with the knot K in four. Small white delta on each partition indicates its direction.
Each part of the film F has a half-twist (not turning over but roughly 90 ) at the beginning.
) at the beginning.
We proceed as shown in Fig. 8,
1. Locate two partitions.
2. Divide the film F in four.
3. Untwist the film F.
4. Cut partitions in Vee shape.
5. Make triangles by shortening strings to a point.
What we say, "shortening strings to a point" is mathematically a mapping of many to one.
The part of the film F for triangle A was the outside at the beginning. So we inverted it to the inside of triangle A (cf. Ch.23 for inversion).
Since the knot K is placed in  , the view of it is just as shown in figures. But, when you observe it together with the film F, do not forget that the film F is on the hyperspher
, the view of it is just as shown in figures. But, when you observe it together with the film F, do not forget that the film F is on the hyperspher  . Triangles at the bottom of Fig. 8 are rearranged in order. (To tell the truth, it is because I drew Fig. 12 first.)
. Triangles at the bottom of Fig. 8 are rearranged in order. (To tell the truth, it is because I drew Fig. 12 first.)
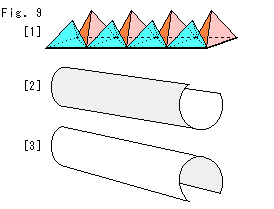
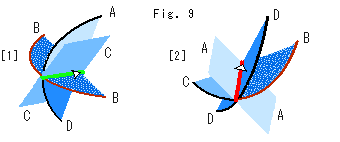 Fig. 9 shows the view around the left end of the green partition observed from the left side.
Fig. 9 shows the view around the left end of the green partition observed from the left side.
Fig. 10 shows the view around the bottom end of the red partition observed from the bottom.
We untwisted and inverted parts of the film F. However, each part of Half Comp  is homeomorphic to the corresponding part of Original Comp
is homeomorphic to the corresponding part of Original Comp  except edges. This exception is due to that triangles A, B, C and D have common points. It will be repaired when we glue tetrahedra T and T' in [Step 2].
except edges. This exception is due to that triangles A, B, C and D have common points. It will be repaired when we glue tetrahedra T and T' in [Step 2].
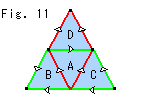 As to the inversion, look at Fig. 11. The triangle A is jointed with triangles B, C and D. Inverted points in the triangle A are smoothly connected to those of triangles B, C and D. So we need not worry about the inversion.
As to the inversion, look at Fig. 11. The triangle A is jointed with triangles B, C and D. Inverted points in the triangle A are smoothly connected to those of triangles B, C and D. So we need not worry about the inversion.
Here we do not pay much attention to topology of the knot K. We will see it later.
We now got four triangles A, B, C and D, each of which has a quarter of Half Comp  (beyond triangles in Fig. 8 excluding vertices).
(beyond triangles in Fig. 8 excluding vertices).
* * * * * * *
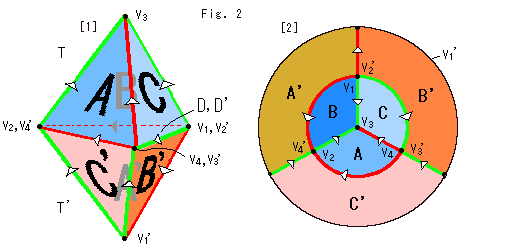
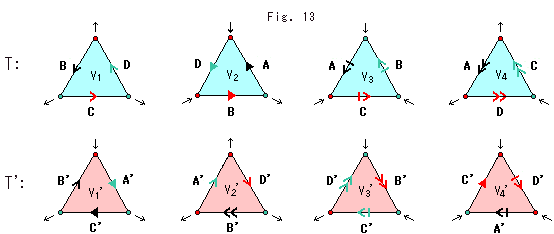
Now we make the tetrahedron T with triangles A, B, C and D as shown in Fig. 12.
Color and direction of edges must meet each other for joining four triangles. This construction is to get a single sheet of the film F again without twisting. Black spots on vertices are points shortened strings. Separated pieces of the knot K get pushed to vertices.
Four parts of Half Comp  are gathered in one again and packed in triangle T (excluding vertices but faces). But this Half Comp
are gathered in one again and packed in triangle T (excluding vertices but faces). But this Half Comp  is not homeomorphic to that of original.
is not homeomorphic to that of original.
Seeing Fig. 12, the rule of homeomorphism is not kept. Number of edges that were former two partitions is now six. "adjoining points are adjoining, and separate points are separate" is not kept. It will be repaired when the tetrahedron T is glued to the tetrahedron T'.
It is not necessary to locate partitions as shown in (*) of Fig. 8 as long as we can get appropriate triangles.
If we could make a cube with some partitions, our story might be different. But it is impossible. Therefore, it is inevitable to get a tetrahedron from the knot K.
* * * * * * *
Now we make another tetrahedron T'.
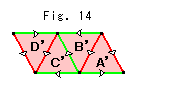 The procedure to get the tetrahedron T' is the same as that of the film F. But it is not necessary to follow the procedure. We make a copy of labels A, B, C and D, and turn over them. And we replace labeles A, B, C and D with A', B', C'and D' respectively as shown Fig. 14. Then we assemble the tetrahedron T' as shown Fig. 13. (You may use a copy of tetrahedron T, and turn over four faces.) The tetrahedron T' (excluding vertices but faces) contains Half Comp
The procedure to get the tetrahedron T' is the same as that of the film F. But it is not necessary to follow the procedure. We make a copy of labels A, B, C and D, and turn over them. And we replace labeles A, B, C and D with A', B', C'and D' respectively as shown Fig. 14. Then we assemble the tetrahedron T' as shown Fig. 13. (You may use a copy of tetrahedron T, and turn over four faces.) The tetrahedron T' (excluding vertices but faces) contains Half Comp  .
.
Back to Top of [Step 1]
this chapter
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[Step 2]
We glue tetrahedra T and T'.
 We have pushed the knot K to vertices of tetrahedra T and T'. We now stick films F and F' each other again without inserting the knot K. And we will get only Topological Comp
We have pushed the knot K to vertices of tetrahedra T and T'. We now stick films F and F' each other again without inserting the knot K. And we will get only Topological Comp  that is a joined space of two Half Comps
that is a joined space of two Half Comps 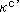 and homeomorphic to the Original Comp
and homeomorphic to the Original Comp  .
.
Imagine that a shrink-wrapping is squeezed and flat excluding contents. Of course, faces must meet as they were at the beginning.
Glue faces A to A', B to B', C to C' and D to D'. Colors and directions of edges must meet each other. It must result to restore edges, one green and one red.
No need to say, glue tetrahedra T and T' by outside to outside. Directions of labels (not faces) are free from identification.
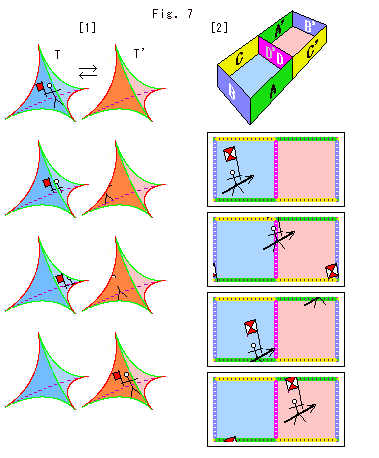
Fig. 15 shows the gluing rule. The gluing is to make edges the same direction at each color, and to identify vertices on each face. But the latter will do.
What we can physically do is only one of gluings in the beginning, A to A' or B to B' or C to C' or D to D'.
Fig. 16 shows a hexahedron with faces D and D' glued. We can do no more gluing by ordinary way. But we do abstractly.
Since this gluing is abstract, we do not think about space where we do. (Do not imagine gluing in the four-dimensional world like SF novels. First of all, any knot gets untied in the four-dimensional world, and we can not make any story.)
As to the abstract gluing, we described some key points in the previous chapter, but we will more inquire into it later. (Do not mis-call the hexahedron in Fig. 16 a regular hexahedron, which is a cube.)
* * * * * * *
When we carry out this abstract gluing,
all vertices of tetrahedra T and T' gather and become a single point, the vertex V. Six red edges are identified and become a single red edge. Similarly six green edges become a single green edge. Each pair of faces is identified and the number of them is totally four. Hence the glued tetrahedra T and T' is now a three-dimensional strange solid with 1 vertex, 2 edges and 4 faces.
 Fig. 17 is what we are forced to draw a picture of this strange solid.
Fig. 17 is what we are forced to draw a picture of this strange solid.
This picture is something like a magic bag. It is transparent but hides the contents except its frame (edges). If it cracked, two visible tetrahedra T and T' come out.
We can catch a glimpse of the strange solid but never full picture. But people in the four-dimensional world can see the entire shape of the strange solid. However, the strange solid itself is absolutely three-dimensional. The reason why it is invisible is because we are unable to draw it.
* * * * * * *
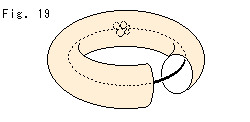
Now, cut off the vertex V of the strange solid as shown in Fig. 19.
 The remainder including faces is Topological Comp
The remainder including faces is Topological Comp  that we have wanted, that is T U T' - V.
that we have wanted, that is T U T' - V.
Topological Comp  has no vertex, 2 edges and 4 faces.
has no vertex, 2 edges and 4 faces.
It is impossible for us with Fig. 19 to judge if Topological Comp  is homeomorphic to Original Comp
is homeomorphic to Original Comp  . We wish to have a model that we could draw in, but none.
. We wish to have a model that we could draw in, but none.
However, though we can not see Topological Comp  by our eyes, we are able to say that it is homeomorphic to Original Comp
by our eyes, we are able to say that it is homeomorphic to Original Comp  because the gluing rule assures to maintain homeomorphism.
because the gluing rule assures to maintain homeomorphism.
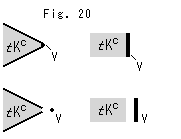 Look at Fig. 20. The cut end of Topological Comp
Look at Fig. 20. The cut end of Topological Comp  has no end point for outward, or an open end point. That is, the boundary belongs to the vertex V. We make it so because the vertex V is an absolute point. Topological Comp
has no end point for outward, or an open end point. That is, the boundary belongs to the vertex V. We make it so because the vertex V is an absolute point. Topological Comp  is an open set.
is an open set.
=======================
Thus as Thurston says,
The complement of figure-8 knot is obtained from (abstractly)
glued two tetrahedra which vertices are eliminated.
And formula (1) is proved (explained), too. Some mathematicians say that it is the demonstration if one convinces oneself. How about you?
=======================
It is possible to get Topological Comp  without making tetrahedra T, T'. All we have to do is that we directly glue triangles of Fig. 8 and 14 following the gluing rule in Fig. 15 and cut vertex V off. However, if we do so, we will miss relations between Topological Comp
without making tetrahedra T, T'. All we have to do is that we directly glue triangles of Fig. 8 and 14 following the gluing rule in Fig. 15 and cut vertex V off. However, if we do so, we will miss relations between Topological Comp  and tetrahedra T, T'. You know,
and tetrahedra T, T'. You know,  is invisible at any rate.
is invisible at any rate.
Remember Original Comp  is vast and boundless complement. But Topological Comp
is vast and boundless complement. But Topological Comp  is a packed object.
is a packed object.
* * * * * * *
Let us review what we have done.
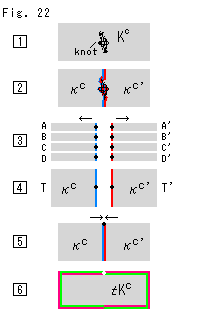 Fig. 22 shows how films F and F' have met and parted.
Fig. 22 shows how films F and F' have met and parted.
 : The first stage (
: The first stage ( - K) that has the knot K and Original Comp
- K) that has the knot K and Original Comp  .
.
 : Films F and F' sandwich the knot K and divide Original Comp
: Films F and F' sandwich the knot K and divide Original Comp  in two, Half Comp
in two, Half Comp 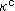 and
and 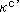 .
.
 : Films F and F' are separated in four triangles each. Every triangle on film F has 1/4 of Half Comp
: Films F and F' are separated in four triangles each. Every triangle on film F has 1/4 of Half Comp 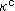 , and every triangle on film F' has 1/4 of Half Comp
, and every triangle on film F' has 1/4 of Half Comp 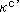 .
.
 : Triangles are joined, and tetrahedra T and T' are formed.
: Triangles are joined, and tetrahedra T and T' are formed.
 : Tetrahedra T and T' are abstractly glued, and films F and F' are stuck again to each other exactly as
: Tetrahedra T and T' are abstractly glued, and films F and F' are stuck again to each other exactly as  . Vertex V is drawn at a corner of films F and F'. The strange solid (T U T') is made.
. Vertex V is drawn at a corner of films F and F'. The strange solid (T U T') is made.
 : Topological Comp
: Topological Comp  (T U T' - V) is surrounded with two edges. A lacked point on the edges is the trace of deleted vertex V. Films F and F' are now useless and erased. Topological Comp
(T U T' - V) is surrounded with two edges. A lacked point on the edges is the trace of deleted vertex V. Films F and F' are now useless and erased. Topological Comp  is an open set.
is an open set.
Fig. 23 below are picture of our story so far.
(a) is continued from the picture bottom left in Fig. 4. (a) is in condition 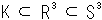 , and (d) is in condition
, and (d) is in condition 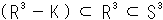 . Symbol "
. Symbol " " is a stressed mark for homeomorphism.
" is a stressed mark for homeomorphism.
Remember that the figure-8 knot we have treated does not pass through a point at infinity.
Back to Top of [Step 1]
[Step 2]
this chapter
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[Step 3]
We are going to geometrilize the complementary space of figure-8 knot. But, [Step 3] is so large that we prepare the following table of contents. You may click and jump to an item, and back here. Or scroll, of course.
[Notes] We must keep it in mind that the deformation is not allowed for a geometrilized object. Any deformation hereafter is just for the convenience of drawing.
Contents in [Step 3]
* * * * * * *
<1> Geometrization and Space
* * * * * * *
We often say, "give a geometric structure" for the geometrization. Geometry is what distances are kept. "kept" means that an object is constant in size and shape, and space has a certain invariable metric.
What we are going to geometrilize is not Topological Comp  . However, as a result, it will be the fact that Topological Comp
. However, as a result, it will be the fact that Topological Comp  is geometrilized. We can not directly geometrilize Topological Comp
is geometrilized. We can not directly geometrilize Topological Comp  . Because Topological Comp
. Because Topological Comp  is abstract, and mathematical expression we have is only
is abstract, and mathematical expression we have is only  = T U T' - V . Therefore we go back to the stage before the gluing. And we decide the shape of tetrahedra T and T'. In other words, we produce what geometrilized.
= T U T' - V . Therefore we go back to the stage before the gluing. And we decide the shape of tetrahedra T and T'. In other words, we produce what geometrilized.
Hyperbolic space is ready prior to the geometrization. And the geometrization is to make an object fit in the existing geometric structure. It is a wrong wording that we will find what the figure-8 knot complement is hyperbolic. Hyperbolic space is ready prior to the figure-8 knot.
Let us make it clear as follows.
Hyperbolic space is the whole hyperbolic space that we grasp as a model.
(The model is Poincare ball for example.)
And
the geometrization is to make tetrahedra T and T' fit the hyperbolic space.
For the geometrization, they say that all we have to do is to use regular ideal tetrahedra (cf. Ch.32) as tetrahedra T and T' with vertices deleted.
Back to Top of [Step 3]
* * * * * * *
<2> Procedure of geometrization
* * * * * * *
To see what geometrization procedure is, we compare regular ideal tetrahedra with what we learned in the previous chapter. The table below contains the figure-8 knot of which column is filled by imitating others. (We are not yet sure if the regular ideal tetrahedra are suitable or not.)
 Glued product in the above table is a representation of what glued abstractly and placed in Euclidean space. As to 3-torus and figure-8 knot, we can not draw any glued product. In general their glued product has no name.
Glued product in the above table is a representation of what glued abstractly and placed in Euclidean space. As to 3-torus and figure-8 knot, we can not draw any glued product. In general their glued product has no name.
The two-holed torus in the above table, the procedure for the geometrization is;
To let 2-D space be hyperbolic plane surface, and
a regular octagon be a hyperbolic regular octagon with 45 inner angles.
inner angles.
We say that it results "Two-holed torus is geometrilized." If we regard the two-holed torus as space, then it results that the space is geometrilized.
After this geometrization,
We can tile the hyperbolic plane surface with this hyperbolic regular
octagon.
We can abstractly tile the hyperbolic plane surface with abstractly
glued one though invisible.
We can represent a double-float (surface) in Euclidean space as glued one.
We also say, "a double-float has hyperbolic geometry" though it does not have surface like Beltrami's Pseudo-sphere. The wording actually indicates the two-holed torus or the hyperbolic regular octagon with 45 inner angles.
inner angles.
Now, our geometrization of figure-8 knot will be as follows if we imitate the two-holed torus;
To let 3-D space be hyperbolic, and
tetrahedra T, T' without vertices be regular ideal tetrahedra.
It will result "The complement of figure-8 knot is geometrilized", won't it?
Back to Top of [Step 3]
* * * * * * *
<3> Vertices of ideal tetrahedra
* * * * * * *
We are going to use ideal tetrahedra if it is okay. First let us think over again about vertices of ideal tetrahedra.
It is known that an ideal tetrahedron has no vertex in Poincare's ball (radius r < 1). But are we sure that it has vertices at infinity  (r = 1)? To tell the truth, such is a fiction. Edges of the ideal tetrahedron (ideal edges) are hyperbolic parallel lines. Everything has been OK'd on the assumption that hyperbolic parallel lines meet each other at infinity. However, it is because of that we have actually not used such a point at infinity though we discussed lots about the infinite.
(r = 1)? To tell the truth, such is a fiction. Edges of the ideal tetrahedron (ideal edges) are hyperbolic parallel lines. Everything has been OK'd on the assumption that hyperbolic parallel lines meet each other at infinity. However, it is because of that we have actually not used such a point at infinity though we discussed lots about the infinite.
Now let us make a new or true definition.
Hyperbolic parallel lines get unlimitedly closed to
but never meet each other whatever they extend.
And we say, "There is no vertex of an ideal tetrahedron at all." Be an opportunist even if you have some objections. We do not intend to deny Lobachevsky's postulate (cf. Ch.5, Ch.6) All in all, we agree
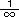 > 0 .
> 0 .
One of worries about using regular ideal tetrahedra cleared up now.
Hereafter we denote regular ideal tetrahedra by t and t'. The regular ideal tetrahedron t corresponds to the tetrahedron T, and so does t' to T'.
Regular ideal tetrahedra t and t' do not depend on vertices of tetrahedra T and T' because vertices were deleted before.
Back to Top of [Step 3]
* * * * * * *
<4> Point at infinity 
* * * * * * *
If we fix one of vertices of tetrahedra T and T' for gluing them, the fixed point will be vertex V. We may choose any point for the fixed point if it was on the knot K at the beginning. But, if it was not, we must find an extra point that does not cause anti-mapping between Original Comp  and Topological Comp
and Topological Comp  . Then the point must be outside of the hypersphere
. Then the point must be outside of the hypersphere  . Does such a point exist?
. Does such a point exist?
Yes, it does. You see, the hypersphere  uses only one of points at infinity. There are infinite points at infinity. They are surrounding the hypersphere
uses only one of points at infinity. There are infinite points at infinity. They are surrounding the hypersphere  as shown in Fig. 24.
as shown in Fig. 24.
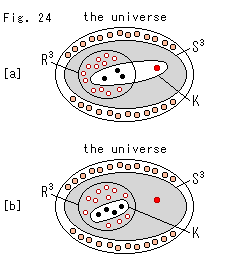
Fig. 24 shows two cases of the first stage. The largest enclosure is the universe. Gray area is Original Comp  . The inner white area is the knot K. Small white and black dots are points in
. The inner white area is the knot K. Small white and black dots are points in  . Pink and red dots are points at infinity. The red dot is only one point at infinity to form the hypersphere
. Pink and red dots are points at infinity. The red dot is only one point at infinity to form the hypersphere  . To distinguish from other points at infinity that are outside of the hypersphere
. To distinguish from other points at infinity that are outside of the hypersphere  it is colored in red. The number of all dots, except the red one, is actually countless.
it is colored in red. The number of all dots, except the red one, is actually countless.
[a]: A point (red) on the knot K is at infinity.
[b]: All points (black) on the knot K are in  and they are within finite distance.
and they are within finite distance.
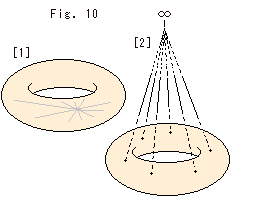
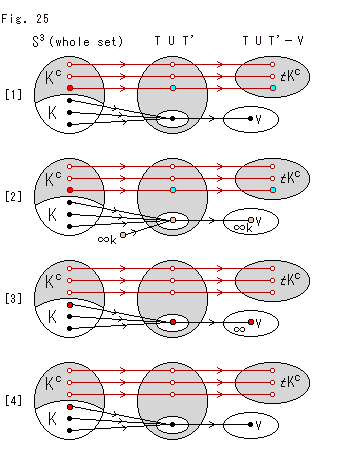 Look at Fig. 25. The hypersphere
Look at Fig. 25. The hypersphere  is the whole set. Black and white dots are always within finite distance. The red dot is the point at infinity
is the whole set. Black and white dots are always within finite distance. The red dot is the point at infinity  , and sky blue dot is a map of the red one. The pink dot is also the point at infinity but different from the red one, and denoted by
, and sky blue dot is a map of the red one. The pink dot is also the point at infinity but different from the red one, and denoted by  k. Brown arrows connect those homeomorphic. The dot in white area of the center row (T U T') is a fixed point for gluing.
k. Brown arrows connect those homeomorphic. The dot in white area of the center row (T U T') is a fixed point for gluing.
[1]: All points on the original the knot K are within finite distance. One of them is chosen for the gluing.
[2]: All points on the original the knot K are within finite distance. But the point at infinity  k in the outside of hypersphere
k in the outside of hypersphere  is chosen for the gluing.
is chosen for the gluing.
[3]: A point on the original knot K is the point at infinity  . And it is chosen for the gluing.
. And it is chosen for the gluing.
[4]: A point on the original knot K is the point at infinity  . But another point that is within finite distance on the original knot K is chosen for the gluing.
. But another point that is within finite distance on the original knot K is chosen for the gluing.
In any case Topological Comp  is homeomorphic to Original Comp
is homeomorphic to Original Comp  .
.
When the last dwelling place of the knot K is at a point of infinity  or
or  k (case [2] or [3]), some says that tetrahedra T and T' under gluing get smaller and smaller, and finally disappear. How do you think?
k (case [2] or [3]), some says that tetrahedra T and T' under gluing get smaller and smaller, and finally disappear. How do you think?
Regular ideal tetrahedra t and t' have no vertex. But it does not mean that only case [3] or [4] is applicable. Because the sky blue dot is an inverted point at infinity. The point is finite, and regular ideal tetrahedra t and t' have it commonly.
We used here  k, but we will normally not distinguish
k, but we will normally not distinguish  k and
k and  unless it is required.
unless it is required.
Back to Top of [Step 3]
* * * * * * *
<5> Dihedral angle
* * * * * * *
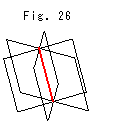 Tetrahedra T and T' together have 6 red edges and 6 green edges to be glued in one red edge and one green edge respectively. That is to say, 6 dihedral angles gather at a place. (A dihedral angle is the angle formed by two intersecting faces.) Therefore, it is quite convenient for us to use regular ideal tetrahedra t and t' because their dihedral angles are exactly 60
Tetrahedra T and T' together have 6 red edges and 6 green edges to be glued in one red edge and one green edge respectively. That is to say, 6 dihedral angles gather at a place. (A dihedral angle is the angle formed by two intersecting faces.) Therefore, it is quite convenient for us to use regular ideal tetrahedra t and t' because their dihedral angles are exactly 60 . That is, 60
. That is, 60 x 6 = 360
x 6 = 360 . (On regular octagons eight of them gather at every vertex because their inner angle is 45
. (On regular octagons eight of them gather at every vertex because their inner angle is 45 .)
.)
Fig. 26 is what we imagine. The same thing happens with green edges at a time. Do not forget that they are abstractly done.
Reason why we choose regular ideal tetrahedra is now cleared with this abstraction.
Back to Top of [Step 3]
* * * * * * *
<6> Manifold
* * * * * * *
Using regular ideal tetrahedra t and t', can we really give geometrical structure to Topological Comp?
It is necessary for the geomerization that Topological Comp  is what is called a manifold. A manifold is a space in which certain geometry stands up equally in neighborhood of every point. That is, a small sphere having a common geometry around any point is available. Let us simply imagine it as something smooth without edges.
is what is called a manifold. A manifold is a space in which certain geometry stands up equally in neighborhood of every point. That is, a small sphere having a common geometry around any point is available. Let us simply imagine it as something smooth without edges.
It is said that
[a] What an open sub set in a manifold is manifold,
and that
[b] What homeomorphic to a manifold is manifold.
 Look at Fig. 27. Hypersphere
Look at Fig. 27. Hypersphere  is manifold. Original Comp
is manifold. Original Comp  is an open sub set in the hypersphere
is an open sub set in the hypersphere  . That is, following [a] above, Original Comp
. That is, following [a] above, Original Comp  is manifold.
is manifold.
And Topological Comp  is homeomorphic to Original Comp
is homeomorphic to Original Comp  . Therefore, following [b] above, we can say that Topological Comp
. Therefore, following [b] above, we can say that Topological Comp  is manifold.
is manifold.
The knot K is a closed set because it is a loop. It includes what passes a point at infinity. (A nmber line extends to a point at infinity and can be considered as a circle with infinite radius, but it is usually regarded as an open set.)
We now understand that Topological Comp  is what we can geometrize. (cf. Euler number on 3-D in [Addenda].)
is what we can geometrize. (cf. Euler number on 3-D in [Addenda].)
* * * * * * *
<7> Comical gluing
* * * * * * *
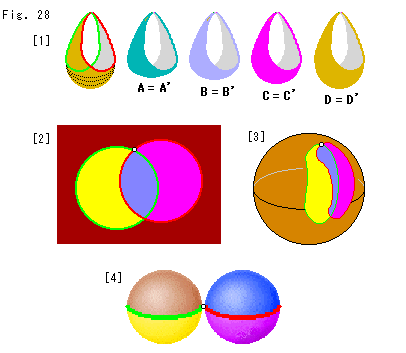 Fig. 28 shows some trial imaginary pictures of Topological Comp
Fig. 28 shows some trial imaginary pictures of Topological Comp  or what regular ideal tetrahedra t and t' are glued. Four faces are classified by color. A small white spot on [2] to [4] is the vestige of deleted vertex V.
or what regular ideal tetrahedra t and t' are glued. Four faces are classified by color. A small white spot on [2] to [4] is the vestige of deleted vertex V.
[1]: The left picture is a finished goods with four layer bags. The three pictures right are bags of glued faces, A to A', B to B', C to C' and D to D'. Each bag has a face with its contents.
[2]: There is an idea that glued two solid balls become a hypersphere. Then, abstractly glued tetrahedra T and T' without vertex V should be something like it. The picture is drawn as a plane based on this idea.
[3]: A picture drawn as a sphere instead of the plane of [2].
[4]: Two balls are chained at lacked point of V. They clearly show 2 edges and 4 faces.
Well, none of these shows how four faces surround Topological Comp  or glued object of regular ideal tetrahedra t and t' are glued.
or glued object of regular ideal tetrahedra t and t' are glued.
Back to Top of [Step 3]
* * * * * * *
<8> Physical gluing
* * * * * * *
Let us try to illustrate a gluing with regular ideal tetrahedra t and t'. We make three trials.
Trial #1
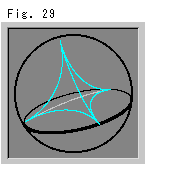 We remember that we could get a double-float by physical gluing the hyperbolic regular octagon. It is because that the hyperbolic regular octagon is two-dimensional and the double-float is three-dimensional. We want to imitate it. But regular ideal tetrahedra are three-dimensional. How can we get a four-dimensional object? It is too much to ask. Nevertheless, we are going to try.
We remember that we could get a double-float by physical gluing the hyperbolic regular octagon. It is because that the hyperbolic regular octagon is two-dimensional and the double-float is three-dimensional. We want to imitate it. But regular ideal tetrahedra are three-dimensional. How can we get a four-dimensional object? It is too much to ask. Nevertheless, we are going to try.
Fig. 29 is a regular ideal tetrahedron in Poincare ball. It has no vertex but here we use a word "vertex" for a convenience to talk. Do not forget it is not a real vertex, please.
Also we refer to Fig. 12 and 13 in [Step 1] that are regarded tetrahedra T and T' as regular ideal tetrahedra t and t' respectively. But we draw edges in straight for simple.
 If we see Fig. 12 carefully, we find that three incoming arrows on the regular ideal tetrahedron t gather at vertex
If we see Fig. 12 carefully, we find that three incoming arrows on the regular ideal tetrahedron t gather at vertex  . Similarly three incoming arrows on the regular ideal tetrahedron t' gather at vertex
. Similarly three incoming arrows on the regular ideal tetrahedron t' gather at vertex  . So we take vertices
. So we take vertices 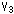 and
and 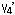 as a point at infinity
as a point at infinity  in the upper side of the upper half space H3+. (You may take
in the upper side of the upper half space H3+. (You may take 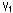 and
and 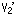 instead.)
instead.)
Here we denote only the upper infinity in the upper half space H3+ by  .
.
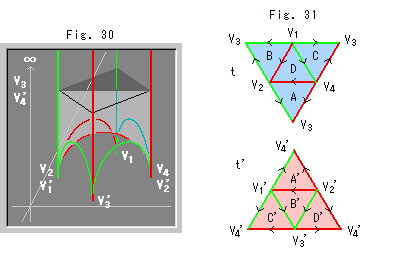
Fig. 30 shows regular ideal tetrahedra t and t' with faces A and A' glued in the upper half space H3+.
Fig. 31 shows unfolded regular ideal tetrahedra t and t'
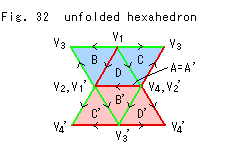
Fig. 32 shows an unfolded ideal hexahedron of Fig. 30. Well, we can not go any more.
Trial #2
Look at Fig. 35 below.
[a]: Pyramid made of [a] in Fig. 33 by gathering four edges that extend to a point at infinity in the upper side of the upper half space H3+. Faces C' and D' are transparent as well as Fig. 33. We mark a point with
in the upper side of the upper half space H3+. Faces C' and D' are transparent as well as Fig. 33. We mark a point with  where vertices
where vertices 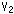 and
and 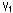 ' met.
' met.
[b]: Edges at  are separated in two groups, red edges
are separated in two groups, red edges  ,
,  and green edges
and green edges  ,
, 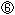 . And the two groups are poled in between. Faces B and B' stand like a book. Their outside surfaces are colored in yellow. When we close the book, we will get glued surface B = B'.
. And the two groups are poled in between. Faces B and B' stand like a book. Their outside surfaces are colored in yellow. When we close the book, we will get glued surface B = B'.
[c]: Faces B and B' are glued. Drawing glued faces A = A' and B = B' is omitted.
That's all, and we give up.
Trial #3
Fig. 36 is to see where we come to deadlock for physical gluing.
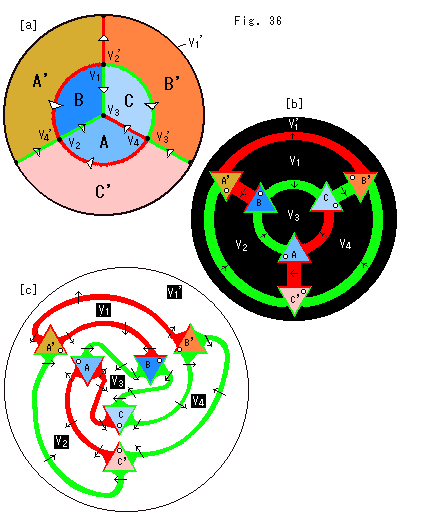
Again we refer to A Topological Picturebook by George K. Francis. A vertex is a point and has no size, and an edge has length and no width. Surprisingly his idea is to let vertices get bigger and widths of edges get wider.
[a]: The unfolded hexahedron made of that of Fig. 16 in [Step 2]. (Glued face D and D' is omitted.)
[b]: Areas painted over with black are deformed vertices. Edges are very deformed as if length and width were exchanged. Small white circles are to indicate relations among vertices, edges and faces.
[c]: Faces A, B and C are turned clockwise to get close to faces A', B' and C' respectively. Every face is twisted so that small white circle marks get face to face. Vertices now are not painted over with black but have black labels.
Now look at this picture carefully. It seems that we can glue face B to face B' like closing a book, C to C' as well. But we can not do the same for faces A and A'. Directions of edges do not meet. If we turn over face A or A', the white marks will not meet. We can not find a way to solve this problem concretely. Here we can not help but give up.
However, George connects vertices through an underground passage and snake-look edges along an overpass. And he glue faces A and A'. Well, his picture is so complicated that it is no more illustration for us.
Back to Top of [Step 3]
* * * * * * *
<9> Mathematical gluing
* * * * * * *
Again we refer to the hexahedron of Fig. 16 in [Step 2] regarding it as that of regular ideal tetrahedra t and t'.
This time, we take the vertex that verices  and
and  joined as infinity
joined as infinity  because directions of four edges together are start from the vertex. And we are going to rely on formulae.
because directions of four edges together are start from the vertex. And we are going to rely on formulae.
Look at Fig. 37 below.
[a]: The hexahedron is laid. We draw edges in straight as usual for simple. Complex numbers are given to positions of vertices (actually no vertex) as shown. We use these complex numbers as names of vertices, too. (Compnents of the verticl axis z are omitted.)
[b]: It is Pyramid that is deformed of [a] for easy setting in the upper half space H3+.
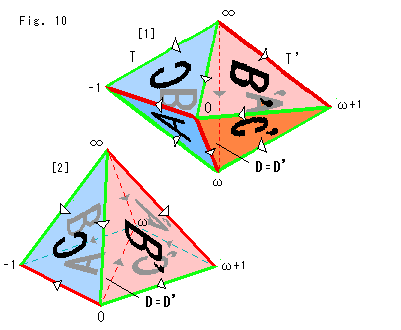
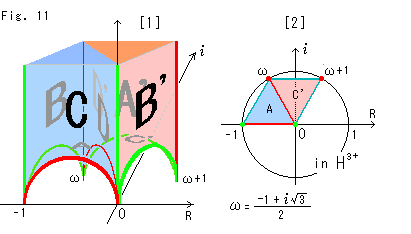
Fig. 38 left shows Pyramid of [b] in Fig. 37 placed in the upper half space H3+. Vertices 0,  +1,
+1,  and -1 are unlimitedly close to the floor (z = 0) of the upper half space H3+. Faces A and C' are parts of hemispherical. Faces B and B' are facing each other. It is up to this stage that can physically be done. The upper area is cut for easy to see.
and -1 are unlimitedly close to the floor (z = 0) of the upper half space H3+. Faces A and C' are parts of hemispherical. Faces B and B' are facing each other. It is up to this stage that can physically be done. The upper area is cut for easy to see.
Fig. 39 is a bird's-eye view of Fig. 38. R is real axis and  is imaginary axis.
is imaginary axis.
Box left shows formulae (Mobius transformations) for gluing.
To get h(z) for gluing face A to face A', do as follows.
Give Z vertices of face A and give W vertices of face A'.
Solve Mobius transformation for a, b, c and d.
Substitute values of a, b, c and d in Mobius transformation.
For f(z) or g(z), do similarly.
These formulae certainly express the gluing in all faces. It frankly agrees such that vertex -1 changes to both vertex  and vertex 0 and also that both vertices -1 and
and vertex 0 and also that both vertices -1 and  change to common vertex
change to common vertex 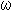 +1. It treats what is physically impossible without any difficulty. There is no mathematical contradiction at all!
+1. It treats what is physically impossible without any difficulty. There is no mathematical contradiction at all!
However, it expresses only the gluing procedure. It is the same as verbal description. And it says nothing about the result of the gluing. If we refer to an advanced mathematical way, we have to go into more abstract area. That is, we see nothing.
Now we understand that we have no choice but to frankly accept the magical result through powerful imagination.
Back to Top of [Step 3]
* * * * * * *
<10> Abstract gluing
* * * * * * *
Gluing in geometrization is;
To do it abstractly without distorting the shape.
"without distorting the shape" is an agreement to keep regular ideal tetrahedra t and t' hyperbolic.
It seems to require us powerful imagination. But it is not so much. Put two regular ideal tetrahedra t and t' in front of you, and guess as if they are glued. You might be standstill if you try to imagine the process or result of the gluing at a time.
There are two ways of understanding the result of abstract gluing.
(dynamic view)
To trace a point following concrete result, e.g. one leaving t
reappears in t'.
(static view)
To accept abstract result as it is, e.g. two edges and four faces.
We pay attention to how it works or what nature it has rather than its appearance or mechanism.
Back to Top of [Step 3]
* * * * * * *
<11> Hyperbolic?
* * * * * * *
Is it obvious that what we get by the geometrization with regular ideal tetrahedra t and t' is hyperbolic?
Yes, it is. Because the way of the abstract gluing of regular ideal tetrahedra t and t' is done without distorting them.
That is,
What we make from hyperbolic object without distortion is hyperbolic.
Besides,
since we can choose only regular ideal tetrahedra t and t' for tetrahedra T and T',
we say that;
Geometry that we can get by the geometrization is only hyperbolic.
Now it is cleared up that Geometric Comp has hyperbolic geometry.
Here after let us use symbol  for Geometric Comp.
for Geometric Comp.
Be that as it may, we wish to directly see if Geometric Comp  itself is hyperbolic. However, only the above idea is available.
itself is hyperbolic. However, only the above idea is available.
Back to Top of [Step 3]
* * * * * * *
<12> Slicing, and Symbolic diagram
* * * * * * *
What will come out if we slice Geometric Comp  ? We are sure that something we can see comes out. If we cut Geometric Comp
? We are sure that something we can see comes out. If we cut Geometric Comp  in opposite way of gluing, we will get regular ideal hexahedra t and t'. But it is not what we want. Since the object is three dimensional, we think we can cut it with an ordinary knife. But, sorry to say, author does not know how to do it at this moment.
in opposite way of gluing, we will get regular ideal hexahedra t and t'. But it is not what we want. Since the object is three dimensional, we think we can cut it with an ordinary knife. But, sorry to say, author does not know how to do it at this moment.
Therefore we slice tetrahedra T and T' individually and glue slices. And then we will think of an appearance of Geometric Comp  .
.
First we see the knot K that was transformed into vertex V, which was cut off. Let us fumble around the vertex V.
We take tetrahedron T with vertices, and cut around them as shown Fig. 40. It corresponds to a fat knot K like Fig. 40'. Do the same on terahedron T'. Then we get 8 small tetrahedra.
A tetrahedron of which corners are cut off is called a truncated tetrahedron.
Let us define our terms and symbols here we use. (See Fig. 41)
| mini-tetrahedron | --- the small tetrahedron gotten by the truncation, |
| m-base | --- the section of the truncation, the base of the |
| | mini-tetrahedron, |
| vertex mV | --- the vertex of the mini-tetrahedron not on m-base. |
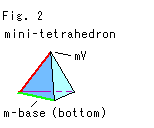
|
The mini-tetrahedron has non-empty interior as well as tetrahedra T, T'.
Now, mark arrows at every m-base edge as shown Fig. 42 below. Any arrow is different from others. Fig. 42' shows arrows of tetrahedron T' following the gluing rule.
It is easy to confuse ourselves if we try to make Fig. 42' at a stroke from Fig. 42, isn't it? Fig. 42' is constructed taking an arrow on every face of tetrahedron T. For example, arrows on face B and face B' are as shown in Fig. 43. See what relations of an arrow on face B with directions of red and green sides, and mark the same arrow where it has the same relations on face B'.
Fig. 44 below shows 8 m-bases with these arrows. They are views from vertices of tetrahedra T and T'. Sky blue ones are of tetrahedron T and pink ones are of tetrahedron T'. Edges of tetrahedra T and T' are shown by small circles at vertices and black thin arrows around triangles. If a thin black arrow is directed inner, the edge directs to the vertex. And if the arrow is directed outer, the edge directs to the opposite.
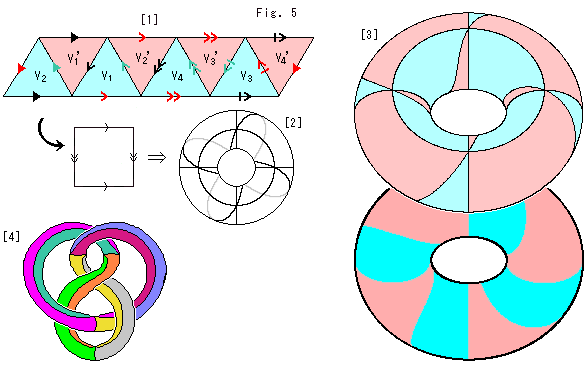
Chain these 8 m-bases to meet their sides as the left picture of Fig. 45.
Now look arrow marks around the chain. It forms a torus (cf. Ch.33). This is the boundary surface of the fat knot K.
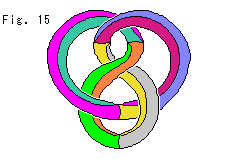
Look at Fig. 46.
[1]: 8 mini-triangles can pasted on a torus. These triangles are very deformed as if rubber films. They form triangulation (cf. Ch.29).
[2]: 8 mini-triangles can also be tiled on the fat knot K.
It is clarified that the torus and the surface of fat knot K are homeomorphic. It is no doubt because both are loops. (They are not isotopic. The figure-8 knot is never called a torus.)
In topology we have no interest in size. Therefore the torus and fat knot K do not change their appearance when we get smaller mini-tetrahedra. It can be interpreted that the torus is a transformed knot K. What we untwisted films F and F' was actually straightening out a tangled the knot K. This situation seems not to change even if the knot K has litte thickness.
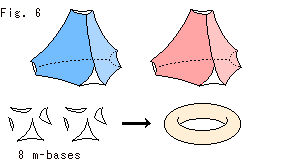
Fig. 47 shows the regular ideal tetrahedra t and t' that are truncated. Eight m-bases (boundaries) are joined edge to edge and form a torus that represents the knot K.
Remember the torus is not a slice of Geometric Comp 
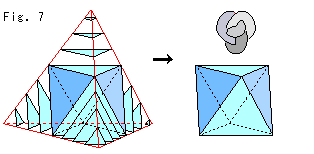
Fig. 48 shows the maximum truncation for slicies, when we get an octahedron. And the knot K is full fat with 8 maximum m-bases.
Due to the maximum truncation, we can not make whole slicing.
Let us go back to Fig. 45.
Fig. 49 shows 3-D view of mini-tetrahedra on the chained m-bases.
Fig. 49' is an abstract picture made from Fig. 49. Vertices mV are gathered at a point, and opposite faces of the pyramid are abstractly glued to each other. Let us call this pyramid missing vertex V of Topological Comp  . The missing vertex V is of course not in the shape of a pyramid.
. The missing vertex V is of course not in the shape of a pyramid.
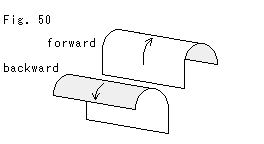
Vertices mV in Fig. 45 are in reader's side. To get the torus in the shape of donut, we first make a cylinder by rolling up the square forward (beyond the screen) or backward (reader's side) as shown Fig. 50. If we consider that the front surface is different from the back, we must choose either forward rolling or backward.
Look at Fig. 51 drawn by force.
[a]: A torus made of the square rolled up backward. The missing vertex V is abstractly packed inside of the torus. That is, in this case, the torus is a solid torus. The picture looks that the missing vertex V is sitting in a small area, but actually it occupies whole inside of the torus. You should imagine so.
[b]: A torus made of the square rolled up forward. The missing vertex V is abstractly stand on outside of the torus. It looks the missing vertex V is floating in midair, but actually it sits on the entire surface of torus.
Both of above imagination are correct, but [b] is better.
Look at Fig. 52. Here we apply the idea of [a] in Fig. 51. The torus is not solid but tubular (hollow) and partially cut to expose the inside for observation. The core is a thin knot K after tetrahedra T and T' were glued.
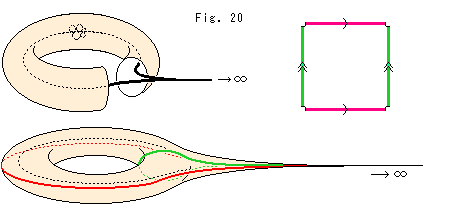 Fig. 53 shows when the knot K passes a point at infinity
Fig. 53 shows when the knot K passes a point at infinity  .
.
The core extends to the point at infinity  , and the torus will have a cusp. The square with arrows lacks corners because the cusp has an open end point just like a number line.
, and the torus will have a cusp. The square with arrows lacks corners because the cusp has an open end point just like a number line.
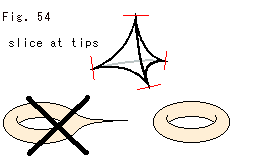
Look at Fig. 54. Let us use regular ideal tetrahedra t and t', and slice at tips. Fig. 54 shows one of the tetrhedra with red lines for shaving. Fig. 53 is correct, however, it should not be applied to ideal tetrahedra. Because ideal tetrahedra have no vertices. Therefore, we get an honest torus from tips, too.
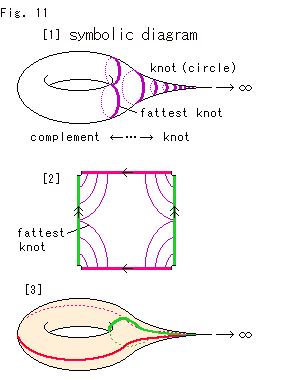
We reduce dimensions of the tetrahedra T and T' for a symbolic diagram or a schematic diagram like Fig. 56. The torus (surface) with a cusp symbolizes the Topological Comp  that is 3-dimesional. Red circles represent tori of knot K with various thickness. The circle is 1-dimensional and the torus is 2-dimensional.
that is 3-dimesional. Red circles represent tori of knot K with various thickness. The circle is 1-dimensional and the torus is 2-dimensional.
We have to stop moving of the circle when it reaches the hole, when the knot K is fattest. To the tip of cusp we can go limitlessly, but the knot K gets thinner and thinner. The complement (surface) never expands to the tip because of the red circle.
However, do not misunderstand Fig. 56. It is not a real appearace of the Topological Comp  .
.
Fig. 56' is the square with lacked corners and red lines that corresponds to Fig. 56.
Back to Top of [Step 3]
* * * * * * *
<13> Appearance of Geometric Comp 
* * * * * * *
If we are required by force to draw Geometric Comp  , we can not help but show something like an eggplant in Fig. 19. However, Geometric Comp
, we can not help but show something like an eggplant in Fig. 19. However, Geometric Comp  has certain shape though in abstract. Therefore, edges are actually hyperbolic straight lines. Remember a number line has no end point but both ends extend to a point of infinity, and we assume that it is a straight line and yet a loop that passes the point at infinity. It reminds us Lobachevsky's idea (Ch.6), doesn't it? Situation on edges of regular ideal tetrahedra t and t' is the same as this number line because all edges extend to infinity. Invisible faces are also hyperbolic.
has certain shape though in abstract. Therefore, edges are actually hyperbolic straight lines. Remember a number line has no end point but both ends extend to a point of infinity, and we assume that it is a straight line and yet a loop that passes the point at infinity. It reminds us Lobachevsky's idea (Ch.6), doesn't it? Situation on edges of regular ideal tetrahedra t and t' is the same as this number line because all edges extend to infinity. Invisible faces are also hyperbolic.
Picture of Geometric Comp  :
:
one lacked vertex (a point at infinity ),
),
two edges that are hyperbolic straight and infinitely extend,
four hyperbolic faces,
two regular ideal tetrahedra t and t' if taken apart.
(Geometric Comp  is homeomorphic to Original Comp
is homeomorphic to Original Comp  but not isotopic.)
but not isotopic.)
The size of Geometric Comp  is, of course, infinity. But its volume is finite. They say that the volume of figure-8 knot is 2.0298832... that is of two regular ideal tetrahedra. A knot is mathematically a curved line, and ordinarily it has no volume but length. However, the volume could be applied to Geometric Comp
is, of course, infinity. But its volume is finite. They say that the volume of figure-8 knot is 2.0298832... that is of two regular ideal tetrahedra. A knot is mathematically a curved line, and ordinarily it has no volume but length. However, the volume could be applied to Geometric Comp  .
.
Back to Top of [Step 3]
* * * * * * *
<14> What happens in the glued tetorahedra?
* * * * * * *
 It is impossible to directly see Geometric Comp
It is impossible to directly see Geometric Comp  . But we can guess it by examining its components. The components are regular ideal tetrahedra t and t' that are regarded as glued. They are just like the square with arrows for a torus. Cf. <10> Abstract gluing.
. But we can guess it by examining its components. The components are regular ideal tetrahedra t and t' that are regarded as glued. They are just like the square with arrows for a torus. Cf. <10> Abstract gluing.
With this idea, we are going to see how Geometric Comp  works or what nature it has.
works or what nature it has.
If a man walks from the inside of the regular ideal tetrahedron t and is going to pass through a face, he appears in the regular ideal tetrahedron t' witout getting out. And if he leaves t', he reappears in t again.
Fig. 57 intends to show this situation.
We can freely go and back between two regular ideal tetrahedra t and t'. It is quite similar to the story of hypersphere made of glued two balls in the previous chapter.
* * * * * * *
<15> In whole hyperbolic space 
* * * * * * *
This section may not be acceptable. But it could be thinkable.
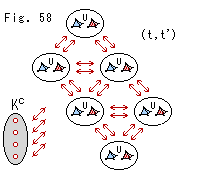
Geometric Comp  is not whole hyperbolic space
is not whole hyperbolic space 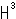 . So we have a choice of location for regular ideal tetrahedra t and t' in Poincare ball
. So we have a choice of location for regular ideal tetrahedra t and t' in Poincare ball 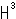 .
.
We tile regular ideal tetrahedra in Poincare ball 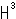 , and assume every pair of them consists of regular ideal tetrahedra t and t' that are regarded as glued. Let us denote the pair by (t, t').
, and assume every pair of them consists of regular ideal tetrahedra t and t' that are regarded as glued. Let us denote the pair by (t, t').
Fig. 58 showes a mapping with arrows are simplified. Every (t, t') is linked not only each other but also to Original Comp  . Say, mapping network.
. Say, mapping network.
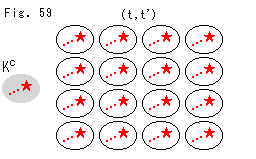 Look at Fig.59. If we put
Look at Fig.59. If we put  in one of (t, t'), it appears in all of (t, t'). In Original Comp
in one of (t, t'), it appears in all of (t, t'). In Original Comp  , too.
, too.
When they move, all of  move simultaneously.
move simultaneously.
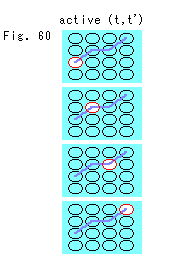
Residents in a certain (t, t') can not go out of it though they appear in all other (t, t'). But it is OK because there is no outside for them who are faithful to the regulation of gluing.
However, if we make an agreement that we measure our location only inside of (t, t') where we stays in, we can go anywhere in Poincare ball  .
.
Fig. 60 shows this situation. Red circled is an active (t, t') where we are. The active (t, t') moves when we move over previous (t, t'). Thus we can move freely.
Back to Top of [Step 3]
* * * * * * *
<16> Summary
* * * * * * *
Fig. 61 below shows our story summarized.
Aiming to the geometrization, we omit unnecessary things that are the strange solid and Topological Comp  .
.
Follow black arrows from left top.
Make the hexahedron of Fig. 16 in [Step 2] from Original Comp  , and cut off its vertices.
, and cut off its vertices.
Replace it with an ideal hexahedron sitting in Poincare ball. Since we use the ideal hexahedron, we do not need to worry about doubling regular ideal tetrahedra that is (t, t'). (If you make the ideal hexahedron directly from Original Comp  , the disposal of vertices can not be done properly.)
, the disposal of vertices can not be done properly.)
Regard it as what is glued. And actually abstract-glue it. Then we get Geometric Comp  . (If you ask us where we do the gluing, we can not help but say, "in your mind".)
. (If you ask us where we do the gluing, we can not help but say, "in your mind".)
This Geometric Comp  fits perfectly to hyperbolic space
fits perfectly to hyperbolic space 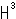 . So we embed it in Poincare ball
. So we embed it in Poincare ball 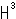 again though it is not necessary. Two edges and four faces gather at the tip of Geometric Comp
again though it is not necessary. Two edges and four faces gather at the tip of Geometric Comp  . And the tip is on the inner side (r < 1) of the surface of Poincare ball
. And the tip is on the inner side (r < 1) of the surface of Poincare ball 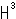 .
.

Fig. 62 is a symbolic full picture of Geometric Comp  of figure-8 knot in consideration of (t, t'). (cf. Ch.32)
of figure-8 knot in consideration of (t, t'). (cf. Ch.32)
This is our finished goods. How do you like it?
Let us modify formula (1) from the viewpoint of the geometrization. It is written as
(2)  - K = t U t'. - K = t U t'. |
| |
| Using our symbols, |
| |
(3)  = =  ( = (t, t')). ( = (t, t')). |
Of course, these should be with appropriate explanations.
If you ask us "Why does hyperbolic geometry come out?", we answer, "Because we intentionally followed the above story." But the essential reason is that figure-8 knot has a character to produce hyperbolic geometry.
Implying this meaning, though (part of) hyperbolic space is Geometric Comp, we say
Figure-8 knot complement is hyperbolic space.
And the definition of a hyperbolic knot is "a knot that has a complement that can be given a metric of constant curvature -1." Naturally Geometric Comp  has curvature -1. So we can say
has curvature -1. So we can say
Figure-8 knot is a hyperbolic knot.
We may say the hyperbolization for the geometrization since our aim is to find the hyperbolic geometry in an object.
Back to Top of [Step 1]
[Step 2]
[Step 3]
this chapter
-*- -*- -*- -*- -*- -*- -*- -*- -*- -*-
[Addenda]
* * * * * * *
Other pictures of figure-8 knot
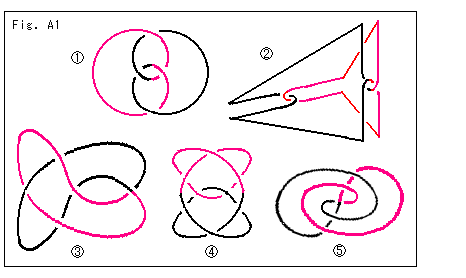
We have more pictures of figure-8 knot that are projected on a plane besides Fig. 1' to 2'' and Fig. 7.
Fig. A1 shows some of them. Symmetric part is colored in red for easy to see.
Figure-8 knot is called an alternating knot. It is a knot with a projection that has crossings that alternate between over and under as one travels around the knot in a fixed direction. All drawings are actually alternating knots though only  looks so.
looks so.  looks like a tetrahedron, doesn't it?
looks like a tetrahedron, doesn't it?  looks as if it carries a balloon inside. In web there are pictures of films,
looks as if it carries a balloon inside. In web there are pictures of films,  in CS284 Project Report and
in CS284 Project Report and 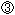 in Soap Films on Knots.
in Soap Films on Knots.
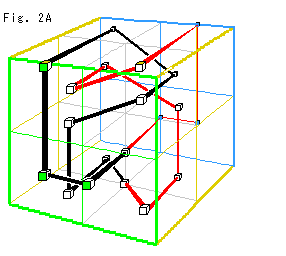
Fig. 2A is the figure-8 knot drawn in a jungle gym. Small cubes show digitized points on the knot K. The coloring outer frame of the jungle gym is just for your observation.
Back to Fig. 2
this chapter
* * * * * * *
 Euler number on 3-D
Euler number on 3-D
Let us apply 3-D Euler number to see if Topological Comp  is manifold. We use it here formally without question.
In three-dimension we use a tetrahedralization. (Most people commonly use a term triagulation (cf. Ch.29) for tetrahedralization.) We decompose a solid into tetrahedra so that they have no gap and no intersections. Fig. 5A right is an example of tetrahedralization though it is in
is manifold. We use it here formally without question.
In three-dimension we use a tetrahedralization. (Most people commonly use a term triagulation (cf. Ch.29) for tetrahedralization.) We decompose a solid into tetrahedra so that they have no gap and no intersections. Fig. 5A right is an example of tetrahedralization though it is in  . The formula of 3-D Euler number
. The formula of 3-D Euler number  is
is
 = v - e + f - s
= v - e + f - s
where
s is number of decomposed tetrahedra.
The right side is in dimensional order as well as 2-D Euler number. However, 3-D Euler number does not tell us characters of a solid as 2-D Euler number does. Because 3-D Euler number is not topological invariant. Yet, it is certain that the solid is a 3-manifold if 3-D Euler number is zero. (The converse may not be true.)
The strange solid T U T' has v = 1, e = 2, f = 4. And s = 2 because it consists of two tetrahedra.
Then
 = 1 - 2 + 4 - 2 = 1.
= 1 - 2 + 4 - 2 = 1.
It is not zero. the strange solid T U T' is not a manifold.
On Topological Comp  T U T' - V, v = 0.
T U T' - V, v = 0.
And
 = 0 - 2 + 4 - 2 = 0.
= 0 - 2 + 4 - 2 = 0.
That is, Topological Comp  is a manifold. (Topologists love manifolds very much, and want cut off vertices earlier as possible.)
is a manifold. (Topologists love manifolds very much, and want cut off vertices earlier as possible.)
Back to <6> Manifold in [Step 3]
this chapter
* * * * * * *
Other hyperbolic knots
There are many hyperbolic knots besides figure-8 knot. You may visit Hyperbolic knot census.
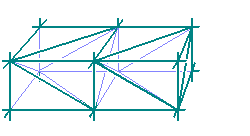
Also friends of a knot called links have hyperbolic structure. Typical examples are Whitehead link and Borromean ring. But they use regular ideal octahedra for geomerization.
Fig. 6A is Whitehead link which 3-D picture is copied from Fancy Knots and Links.
Fig. 7A is Borromean ring which 3-D picture is copied from The KnotPlot Site
Back to this chapter
* * * * * * *
tripus
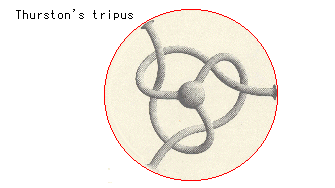
There is a monster of figure-8 knot called Thrston's tripus or knotted Y. Fig. 8A is the monster.
Fig. 8'A is a revised picture of Fig. 36 (Trial #3 in <8> Physical gluing) that is the unfolded hexahedron made of that in to Fig. 16 in [Step 2]. It has new marks only on faces. Edges are not distinguished by color. (If we could apply this trick to [b] in Fig. 36, we can glue face A to face A'.) Now glue two tetrahedra, then their vertices grow into three legs. It is rather complicate. Erase glued faces, pull out vertices, join edges and let them snake through underpasses, ... Let us enjoy the picture without question at this moment.
Back to this chapter
* * * * * * *
I asked Bill Thurston before writing this story. (He knew I am an amateur.)
Q: Topology does not care of distances. On the other hand, geometry needs
distances. Do you newly define a distance for the geometrization?
A: No. It is a kind of translation just like English to Japanese.
Well, I could feel something true.
Also I asked George K. Francis.
Q: Why does hyperbolic geometry come out?
A: Do not say, "Why". You should ask "How".
* * * * * * *
In short
Abstract gluing is a key point for us. How to understand it is a question. The answer is nothing but imagination. Nevertheless, what we get by the imagination really exists! (Mathematicians do not discuss existence, though.)
* * * * * * *
Be that as it may, don't you feel something doubtful?
Don't you think the story is too much tricky? You see, hyperbolic geometry is of the universal scale. It comes out from figure-8 knot in your hand. It sounds mysterious.
Frankly speakig, I myself feel, "Is that mathematics?"
Some mathematicians say that we need powerful mathematics. However, it gets more accuracy only. Mathematical accuracy does not make us be relieved. What we need is explicit explanations.
* * * * * * *
Now we have come to the most advanced mathematics in 1978. You might think 1978 is old. But it is not true. Surprisingly it is still fresh. They also say that figure-8 knot relates to what is called Poincare conjecture.
Mathematical near future is full of romance. We are now in the Revolution Eve!
Back to Top of [Step 1]
[Step 2]
[Step 3]
this chapter
[Back] [Next] [Contents]
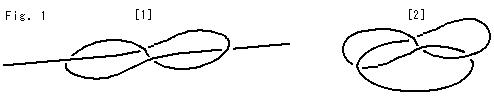



 We consider films F and F' as spheres because they expand to infinity
We consider films F and F' as spheres because they expand to infinity  Fig. 6 is a photo of the knot K with a film. It is made of a metal wire dipped in shampoo. Well, it is hard to see, isn't it? We are able to see a certain part of the film but not the whole. It is such that the wire with the film goes through another part of the film (the wire crosses in two-level and the film intersects itself). The film is transparent but it is not easy to see a construction beyond the film surface.
Fig. 6 is a photo of the knot K with a film. It is made of a metal wire dipped in shampoo. Well, it is hard to see, isn't it? We are able to see a certain part of the film but not the whole. It is such that the wire with the film goes through another part of the film (the wire crosses in two-level and the film intersects itself). The film is transparent but it is not easy to see a construction beyond the film surface. Fig. 7 shows another view of the knot K. It may melt your doubt. A film crosses itself and twists, but it has the front and back. It is also obvious if you recall that the knot K is a 3-D loop.
Fig. 7 shows another view of the knot K. It may melt your doubt. A film crosses itself and twists, but it has the front and back. It is also obvious if you recall that the knot K is a 3-D loop. Figure (*) upper right shows the entire kno K with red and green partitions that will divide the film F together with the knot K in four. Small white delta on each partition indicates its direction.
Figure (*) upper right shows the entire kno K with red and green partitions that will divide the film F together with the knot K in four. Small white delta on each partition indicates its direction. Fig. 9 shows the view around the left end of the green partition observed from the left side.
Fig. 9 shows the view around the left end of the green partition observed from the left side. As to the inversion, look at Fig. 11. The triangle A is jointed with triangles B, C and D. Inverted points in the triangle A are smoothly connected to those of triangles B, C and D. So we need not worry about the inversion.
As to the inversion, look at Fig. 11. The triangle A is jointed with triangles B, C and D. Inverted points in the triangle A are smoothly connected to those of triangles B, C and D. So we need not worry about the inversion.
 The procedure to get the tetrahedron T' is the same as that of the film F. But it is not necessary to follow the procedure. We make a copy of labels A, B, C and D, and turn over them. And we replace labeles A, B, C and D with A', B', C'and D' respectively as shown Fig. 14. Then we assemble the tetrahedron T' as shown Fig. 13. (You may use a copy of tetrahedron T, and turn over four faces.) The tetrahedron T' (excluding vertices but faces) contains Half Comp
The procedure to get the tetrahedron T' is the same as that of the film F. But it is not necessary to follow the procedure. We make a copy of labels A, B, C and D, and turn over them. And we replace labeles A, B, C and D with A', B', C'and D' respectively as shown Fig. 14. Then we assemble the tetrahedron T' as shown Fig. 13. (You may use a copy of tetrahedron T, and turn over four faces.) The tetrahedron T' (excluding vertices but faces) contains Half Comp  We have pushed the knot K to vertices of tetrahedra T and T'. We now stick films F and F' each other again without inserting the knot K. And we will get only Topological Comp
We have pushed the knot K to vertices of tetrahedra T and T'. We now stick films F and F' each other again without inserting the knot K. And we will get only Topological Comp 
 Fig. 17 is what we are forced to draw a picture of this strange solid.
Fig. 17 is what we are forced to draw a picture of this strange solid. The remainder including faces is Topological Comp
The remainder including faces is Topological Comp  Look at Fig. 20. The cut end of Topological Comp
Look at Fig. 20. The cut end of Topological Comp  Fig. 22 shows how films F and F' have met and parted.
Fig. 22 shows how films F and F' have met and parted.


 Look at Fig. 25. The hypersphere
Look at Fig. 25. The hypersphere  Tetrahedra T and T' together have 6 red edges and 6 green edges to be glued in one red edge and one green edge respectively. That is to say, 6 dihedral angles gather at a place. (A dihedral angle is the angle formed by two intersecting faces.) Therefore, it is quite convenient for us to use regular ideal tetrahedra t and t' because their dihedral angles are exactly 60
Tetrahedra T and T' together have 6 red edges and 6 green edges to be glued in one red edge and one green edge respectively. That is to say, 6 dihedral angles gather at a place. (A dihedral angle is the angle formed by two intersecting faces.) Therefore, it is quite convenient for us to use regular ideal tetrahedra t and t' because their dihedral angles are exactly 60 Look at Fig. 27. Hypersphere
Look at Fig. 27. Hypersphere 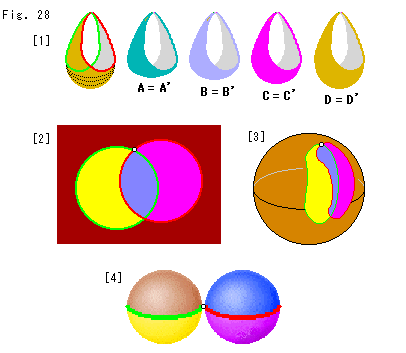 Fig. 28 shows some trial imaginary pictures of Topological Comp
Fig. 28 shows some trial imaginary pictures of Topological Comp  We remember that we could get a double-float by physical gluing the hyperbolic regular octagon. It is because that the hyperbolic regular octagon is two-dimensional and the double-float is three-dimensional. We want to imitate it. But regular ideal tetrahedra are three-dimensional. How can we get a four-dimensional object? It is too much to ask. Nevertheless, we are going to try.
We remember that we could get a double-float by physical gluing the hyperbolic regular octagon. It is because that the hyperbolic regular octagon is two-dimensional and the double-float is three-dimensional. We want to imitate it. But regular ideal tetrahedra are three-dimensional. How can we get a four-dimensional object? It is too much to ask. Nevertheless, we are going to try. If we see Fig. 12 carefully, we find that three incoming arrows on the regular ideal tetrahedron t gather at vertex
If we see Fig. 12 carefully, we find that three incoming arrows on the regular ideal tetrahedron t gather at vertex 





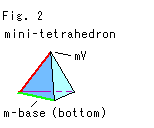



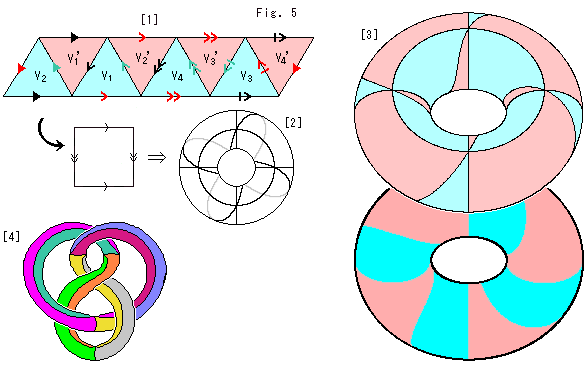






 Fig. 53 shows when the knot K passes a point at infinity
Fig. 53 shows when the knot K passes a point at infinity 

 It is impossible to directly see Geometric Comp
It is impossible to directly see Geometric Comp 
 Look at Fig.59. If we put
Look at Fig.59. If we put 




 Euler number on 3-D
Euler number on 3-D
